СОДЕРЖАНИЕ

ЦЕЛЬ РАБОТЫ……………………………………………………...……4

ОБОРУДОВАНИЕ …………………………………………………….…4

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ……………………………………………...5

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

1. Описание экспериментальной установки…………………..…...10

2. Выполнение измерений……………………….…………...……..11

3. Обработка результатов измерений …………….………………..12

КОНТРОЛЬНЫЕ ВОПРОСЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ ПОДГОТОВКИ К ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ…………………………...…………...…………………….......13

БИБЛИОГРАФИЧЕСКИЙ СПИСОК…………………………………..15

ЦЕЛЬ РАБОТЫ: ознакомиться с определением удельного заряда частицы методом магнетрона и определить удельный заряд электрона.

Оборудование

1. Регулируемый источник постоянного напряжения «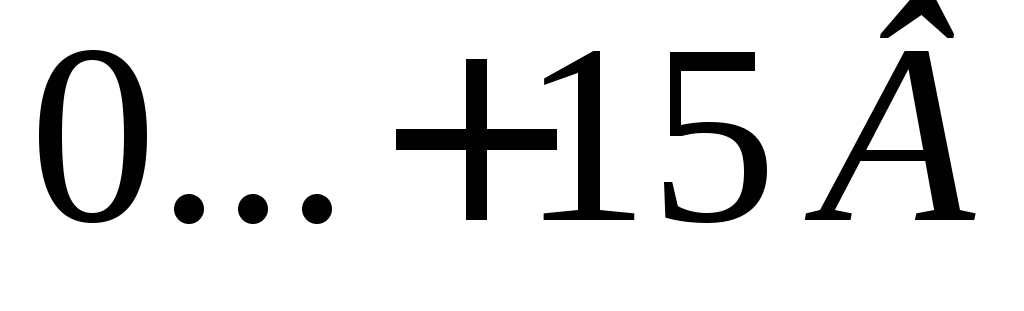» на плате «Блок генераторов».

2. Стабилизированые источники постоянного напряжения «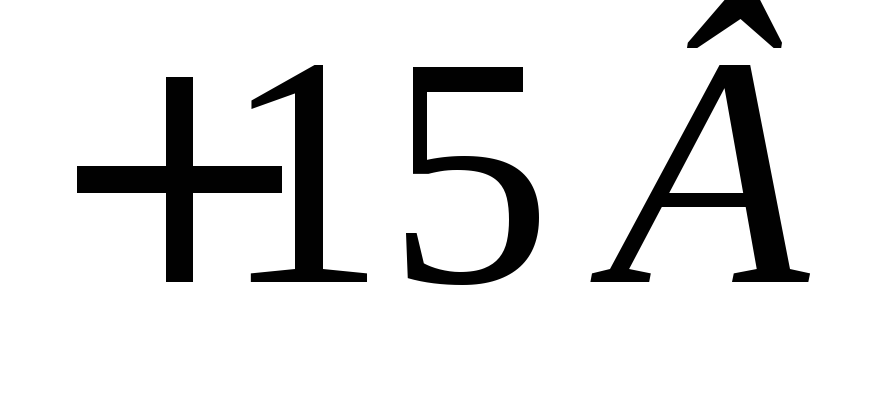» и «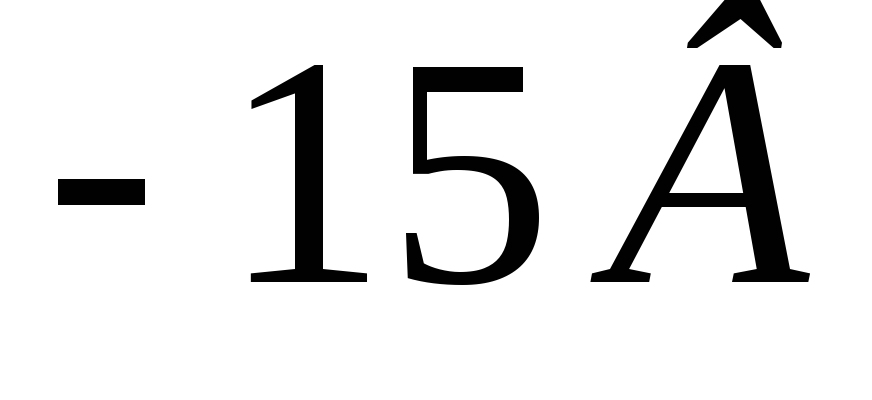» на плате «Блок генераторов».

3. Блок мультиметров.

4. Миниблок «Магнетрон».

5. Красные и синие соединительные провода.

Теоретическая часть

Электрические и магнитные поля, воздействуя на движущиеся заряженные частицы, изменяют их скорость и траекторию. В электрическом поле напряженности на частицу, обладающую зарядом , действует сила

. (1)

В магнитном поле на движущуюся заряженную частицу действует сила Лоренца

, (2)

где – скорость движения частицы;– вектор магнитной индукции.

Модуль силы Лоренца определяется по формуле

, (3)

где – угол между векторамии.

Направление силы Лоренца можно определить либо поправилу правого винта (правилу буравчика), либо по правилу левой руки.

П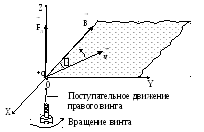равило правого винта: сила Лоренца , действующая на движущийся положительный заряд , направлена перпендикулярно к плоскости, в которой лежат векторыи, в сторону поступательного движения правого винта, если его поворачивать кратчайшим путем от векторак вектору(рис. 1) (для отрицательного заряданаправление силыбудет противоположным).

Рис. 1. Применение правила правого винта для определения направления силы Лоренца , действующей на положительный заряд, по известным направлениям векторов скорости зарядаи магнитной индукциив месте его нахождения (илежат в плоскостиXOY)

Правило левой руки: если левую руку расположить так, чтобы вектор магнитной индукции входил в ладонь, а четыре сомкнутых пальца были направлены по составляющей вектора скоростиположительного заряда , перпендикулярной к магнитной индукции, то отогнутый на 90 большой палец покажет направление силы Лоренца , действующей на этот заряд (рис. 2) (для отрицательного заряда –q направление силы будет противоположным).

Уравнение движения частицы в пространстве, где имеются и электрическое и магнитное поля, согласно второму закону Ньютона имеет следующий вид:

. (4)

Подставляя (1) и (2) в (4), получаем

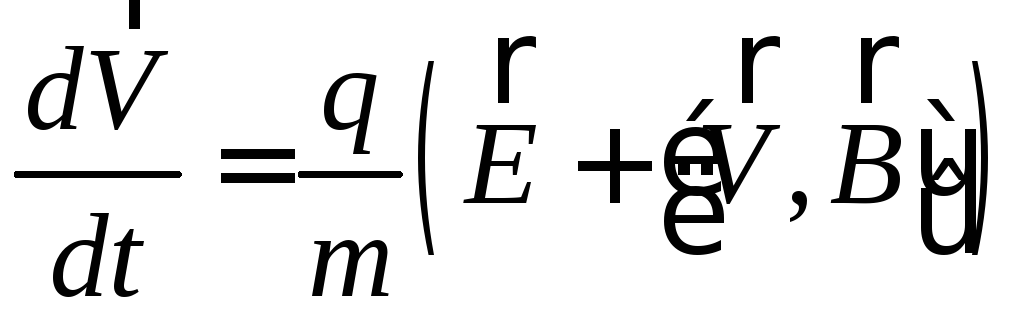. (5)

Уравнение (5) показывает, что движение заряженной частицы в силовых полях зависит от отношения , которое называетсяудельным зарядом данной частицы. Следовательно, изучая движение различных заряженных частиц в электрическом и магнитном полях, можно определить удельный заряд частицы и тем самым получить сведения о природе частиц.

Удельный заряд электрона можно определить различными методами. В данной работе для определения удельного заряда электрона используется метод магнетрона.

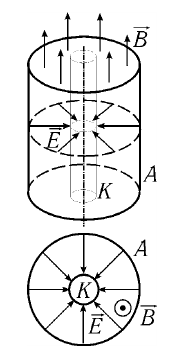Магнетрон– это двухэлектродная электронная лампа (диод), в которой управление током осуществляют внешним магнитным полем. Это поле создается соленоидом, внутри которого расположена лампа. Накаливаемый катод К и холодный анод А лампы имеют форму коаксиальных (соосных) цилиндров (рис. 3). Нагретый до высокой температуры катод К испускает электроны (явление термоэлектронной эмиссии), которые достигают анода А, имеющего более высокий потенциал, чем катод.

Линии электрического поля внутри магнетрона направлены радиально от анода к катоду, а постоянное магнитное поле направлено вдоль оси катода. Таким образом, магнитное и электрическое поля взаимно перпендикулярны. Напряженность поля E максимальна у катода. В случае, если катод имеет форму тонкой нити, величина E, пропорциональная , быстро уменьшается с ростом расстояния от катода. Поэтому изменение скорости электронов до значения, равного , происходит в основном вблизи катода, а при дальнейшем его движении можно считать скорость практически постоянной. Рис.3. Лампа

По закону сохранения энергии электрон с величиной заряда и массой, прошедший в электрическом поле разность потенциалов , приобретает кинетическую энергию

(6)

и имеет скорость

. (7)

В отсутствие магнитного поля электроны, испущенные катодом, движутся под действием электрического поля прямолинейно в радиальных направлениях. При этом в анодной цепи протекает ток, величина которого зависит от анодного напряжения и тока накала катода. При помещении лампы в магнитное поле на движущиеся электроны действует сила Лоренца. Она перпендикулярна к линиям, т.е. лежит в одной плоскости с вектором скорости электрона, нормальна ему и сообщает частице центростремительное ускорение. Согласно второму закону Ньютона

, (8)

где – радиус дуги окружности, по которой движется электрон.

Учитывая, что в лампе , уравнение (8) можно переписать следующим образом:

, (9)

откуда вытекает выражение для радиуса траектории электрона

. (10)

Таким образом, электрон в магнетроне будет двигаться по окружности, радиус которой уменьшается с ростом индукции магнитного поля. На рис. 4 показано, как изменяются траектории движения электрона в цилиндрическом магнетроне по мере увеличения магнитной индукции.

Существует критическое значение магнитной индукции , при котором, как показано на рис. 4, траектории электронов касаются поверхности анода, а их радиус

, (11)

где – радиус анода.

Рис. 4. Траектории движения электрона при увеличении магнитной индукции

Согласно соотношениям (7), (10) и (11) значение зависит от скорости электрона и соответствующего ей анодного напряжения :

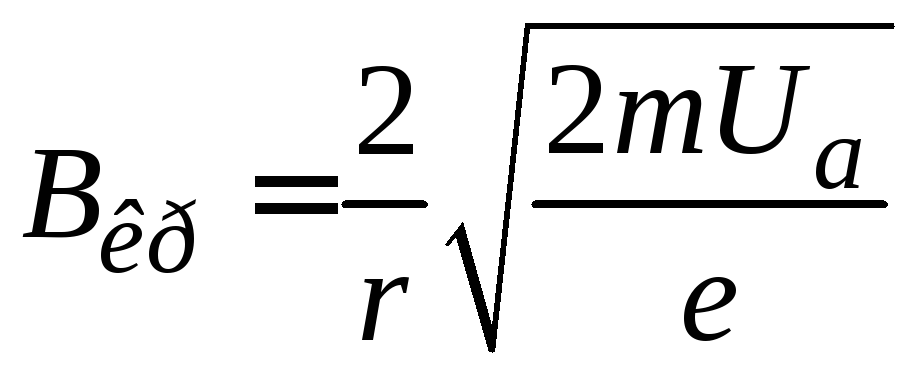. (12)

Если величина , то все электроны достигают анода и анодный токимеет такое же значение, как и в отсутствии магнитного поля (горизонтальный участок графика на рис. 4). Если, то электроны не долетают до анода и ток через лампу равен нулю. Притокдолжен резко снижаться (пунктирная линия на графике рис. 4), однако наблюдается плавный ход кривой. Это обусловлено рядом причин: неточная коаксиальность катода и анода, краевые эффекты, вылет электронов из катода с различными скоростями и др.

Определив критическое значение индукции магнитного поля и использовав соотношение (12), можно рассчитать удельный заряд электрона по формуле

. (13)

Индукцию B вычисляют по формуле для поля короткого соленоида:

. (14)

ЗдесьГн/м – магнитная постоянная;I – ток, текущий в обмотке; N –число витков соленоида; – длина обмотки; и– углы, показанные на рис. 5 при размещении лампы в центре соленоида

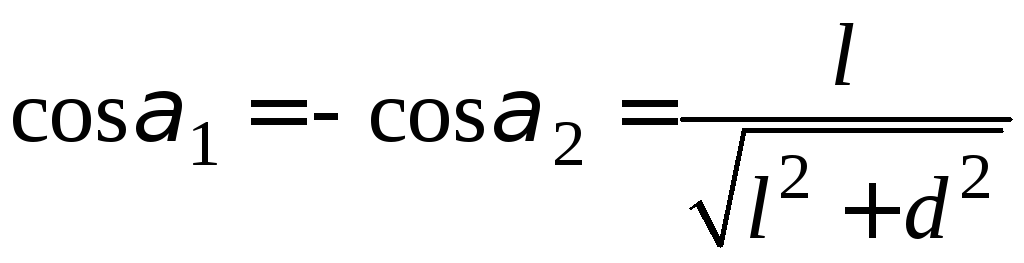, (15)

где – диаметр соленоида.

Подставляя значения косинусов в формулу (14), получаем критическую величину магнитной индукции

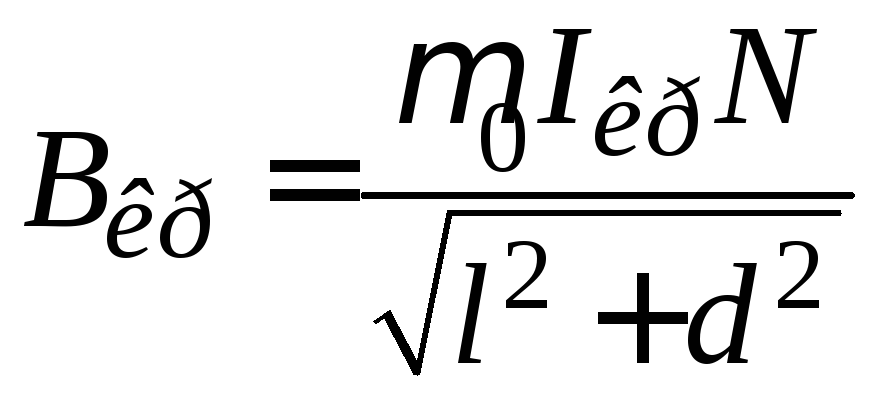, (16)

где – значение тока в соленоиде, соответствующее критическому значениюРис. 5. Соленоид

магнитной индукции .

С учетом выражения (16) расчетная формула (13) для определения удельного заряда электрона принимает следующий вид:

. (17)

Для определения критического тока используют экспериментальную зависимость анодного тока от тока в соленоиде(рис. 6, а), которая по виду подобна зависимости: при критическом токе в соленоиде наблюдается резкое снижение анодного тока.

Крутизну кривой показывает отношение приращений анодного тока и тока в соленоиде.При этом максимум кривой(рис. 6, б) соответствует искомому значению.

Рис. 6. Определение критического тока