3. Связь напряженности с потенциалом в электростатическом поле

В разд. 2 получены формулы (12) и (14), позволяющие по напряженности находить разность потенциаловили потенциалыдля точек электростатического поля. Теперь найдем обратную зависимость, позволяющую определять напряженностьполя по его потенциалу.

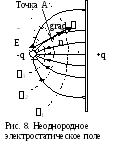Рассмотрим неоднородное электростатическое поле, образованное, например, отрицательным точечным зарядом -q и проводящей плоскостью с зарядом +q (рис. 8).

В произвольной точке А с помощью единичного вектора зададим направление, перпендикулярное к эквипотенциальной поверхности и касательное линии напряжен-ности. Векторнаправлен в сторону возрастания потенциала, то есть противоположно вектору. Перепишем выражение (13) для случая элементарного перемещения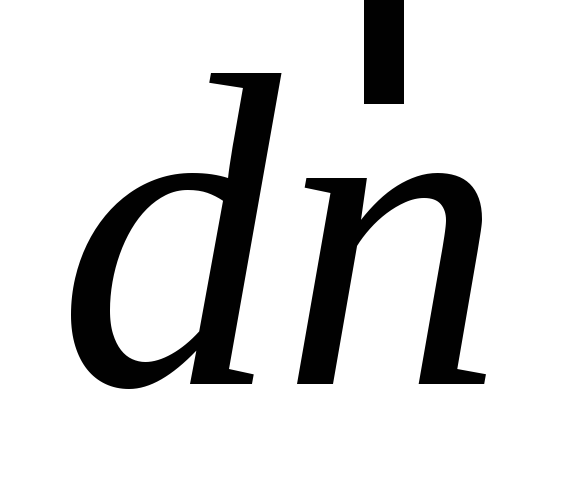вдоль линии напряженности в направлении вектора, учитывая, что при этом, а:

. (15)

Из (15) вытекает

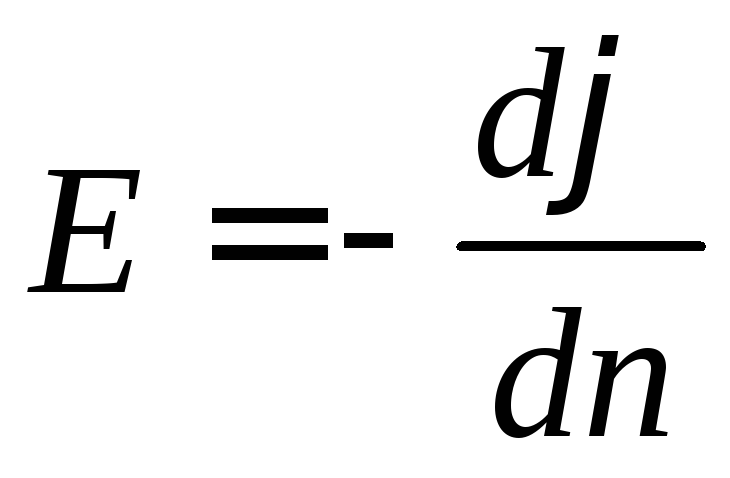(16)

или в векторном виде

. (17)

Вектор называется градиентом потенциала, поэтому выражение (17) обычно записывается в виде

. (18)

12