Семинар 9

Операции над векторами, скалярное, векторное и смешанное произведения векторов.

Вводная информация

Определение геометрического вектора.

Определение. Вектором (геометрическим вектором) называется направленный прямолинейный отрезок, т.е. отрезок, имеющий определенную длину и определенное направление. Если - начало вектора, а - его конец, то вектор обозначается символом или . Вектор () называется противоположным вектору .

Длиной вектора или его модулем называется длина отрезка и обозначается . Вектор, длина которого равна нулю, называется нулевым вектором и обозначается . Вектор, длина которого равна единице, называется единичным вектором. Единичный вектор, направление которого совпадает с направлением вектора , называется ортом этого вектора и обозначается .

Векторы и называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Для коллинеарных векторов принято обозначение . Два вектора называются равными (), если они одинаково направлены и имеют одинаковые длины. Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

Операции над векторами.

На множестве векторов вводится бинарная операция, которая называется сложением векторов. Эту операцию можно определить либо правилом параллелограмма (если векторы и , являются сторонами параллелограмма, то их суммой будет вектор , где - четвертая вершина параллелограмма), либо правилом треугольника (если векторы и являются сторонами треугольника, то их суммой называют вектор ).

Легко убедиться в следующих свойствах этой бинарной операции на множестве векторов:

1) ;

2) ; 3) ;

4) .

Следовательно, относительно сложения множество векторов образует абелеву группу.

Произведением вектора на число называется вектор , который имеет длину и направление вектора , если ; направление противоположного вектора к , если . Отметим, что .

Произведение вектора на число обладает свойствами:

1) ;

2) ;

3) .

Множество геометрических векторов с введенными на нем операциями называется векторным пространством.

Координаты вектора.

Рассмотрим пространство с введенной на нем декартовой системой координат. Пусть и - три единичных вектора, исходящих из начала координат в направлениях соответственно декартовых осей и . Эти векторы называются ортами координатных осей. Пусть вектор имеет начало также в точке (начале координат). Спроектируем конец вектора на координатные оси. Полученные проекции можно записать в виде и , где и - углы, которые образует вектор соответственно с координатными осями и . Числа и называются направляющими косинусами вектора . Вектор и его проекции на координатные оси удовлетворяют равенству

.

Тройка векторов называется базисом векторного пространства , а написанное выше равенство – разложением вектора по базису . При этом числа носят название координат вектора относительно базиса . Поскольку координаты вектора относительно данного базиса являются проекциями этого вектора на координатные оси, длина вектора и его координаты связаны формулой

.

Подставляя в эту формулу координаты вектора, выраженные через направляющие косинусы, легко получить равенство

,

которому удовлетворяют направляющие косинусы любого вектора. Заметим, что направляющие косинусы являются координатами орта вектора .

Поскольку координаты вектора полностью его определяют, можно ввести обозначение и заменить введенные операции над векторами операциями над их координатами. Так сложение векторов можно заменить сложением их координат: , т.е. ,

а умножение вектора на число - умножением координат на это число: или .

Равенство векторов на координатном языке предполагает равенство их координат , а коллинеарность - пропорциональность их координат .

Пусть имеются две точки и . Тогда вектор можно записать в виде или . В частности, для радиус-вектора точки имеем формулы или .

Скалярное произведение векторов.

Скалярным произведением векторов и называется число, равное , где - угол между векторами. Это произведение обозначают разными способами

.

Отметим свойства введенного скалярного произведения.

1) (симметричность);

2) (линейность);

3) , причем тогда и только тогда, когда .

Векторное пространство с таким скалярным произведением называется евклидовым пространством. В этом пространстве можно ввести норму (длину) вектора правилом . Для евклидового пространства справедливы следующие теоремы.

Для любых двух векторов и евклидового пространства справедливо неравенство Коши-Буняковского

.

Для любых двух векторов и евклидового пространства с нормой вектора справедливо неравенство треугольника

.

Неравенство Коши-Буняковского позволяет ввести понятие угла между векторами в евклидовом пространстве, для которого

.

Два вектора и называются ортогональными, если . В евклидовом пространстве угол между такими векторами равен . Попарно ортогональны орты координатных осей . Поскольку длины этих векторов считаются равными единице (например, ), базис, состоящий из подобных векторов, называется ортонормированным базисом. Учитывая единичную нормировку таких базисных векторов и их попарную ортогональность, легко показать, что

и

.

Пусть материальная точка перемещается прямолинейно из точки в точку под действием постоянной силы , образующей угол с вектором .

Работа этой силы при перемещении точки на расстояние равна произведению проекции этой силы на направление перемещения на величину перемещения: . Таким образом, скалярное произведение векторов и равно работе силы при перемещении точки на вектор , т.е.

.

Эта формула отражает физическое приложение скалярного произведения. Векторное произведение векторов.

Рассмотрим два вектора и . Векторным произведением этих векторов называется вектор ,

1. равный по величине , где - угол между векторами и ,

2. имеющий направление, определяемое правилом буравчика, ручка которого вращается от вектора к вектору (т.е. вектор перпендикулярен как вектору , так и вектору).

Отметим основные свойства векторного произведения.

1. (антисимметричность).

2. (линейность).

К геометрическим свойствам векторного произведения относят определение коллинеарности векторов и нахождение площади параллелограмма (треугольника).

1. Если векторное произведение векторов и равно нулю, то эти векторы коллинеарны (и наоборот).

2. Площадь параллелограмма, построенного на векторах и , равна длине их векторного произведения: , а площадь соответствующего треугольника - половине его длины: .

В качестве физических приложений можно привести:

1) момент силы относительно точки ;

2) момент импульса относительно точки ;

3) линейная скорость вращения .

Используя свойство линейности векторного произведения и учитывая, что , несложно получить формулу векторного произведения через координаты векторов

.

Смешанное произведение векторов.

Смешанным произведением векторов называют произведение вида

,

т.е. смешанное произведение векторов является числом (скаляром).

Отметим основные свойства смешанного произведения векторов.

1. Смешанное произведение векторов не меняется при их циклической перестановке

.

2. Смешанное произведение векторов не меняется при перемене местами знаков векторного и скалярного умножения

.

Последнее свойство позволяет записывать смешанное произведение в виде (без знаков векторного и скалярного произведений).

3. Смешанное произведение меняет знак при перестановке любых двух векторов, входящих в смешанное произведение, например, .

Используя определение смешанного произведения векторов, не составляет труда получить формулу

,

позволяющую вычислить это произведение через координаты векторов.

Перечислим основные геометрические приложения смешанного произведение векторов.

1. Определение взаимной ориентации векторов в пространстве.

Если , то векторы и образуют правую тройку (буравчик двигается в направлении вектора , если его ручка поворачивается от вектора к вектору ). Если же , то векторы и образуют левую тройку векторов.

2. Установление компланарности векторов.

Ненулевые векторы и компланарны тогда и только тогда, когда их смешанное произведение равно нулю:

=0.

3. Вычисление объема параллелепипеда.

Объем параллелепипеда, построенного на векторах и , равен модулю их смешанного произведения, т.е. .

4. Вычисление объема треугольной пирамиды.

Объем треугольной пирамиды, построенной на векторах и , равен .

5. Вычисление объема треугольной призмы.

Объем треугольной призмы, построенной на векторах и , равен .

Символ Кронекера и символ Леви-Чивита.

При вычислении различных произведений векторов удобно использовать символы, сокращающие объем вычислений. К таким символам относятся символ Кронекера и символ Леви-Чивита. Символ Кронекера обозначается и определяется следующим образом

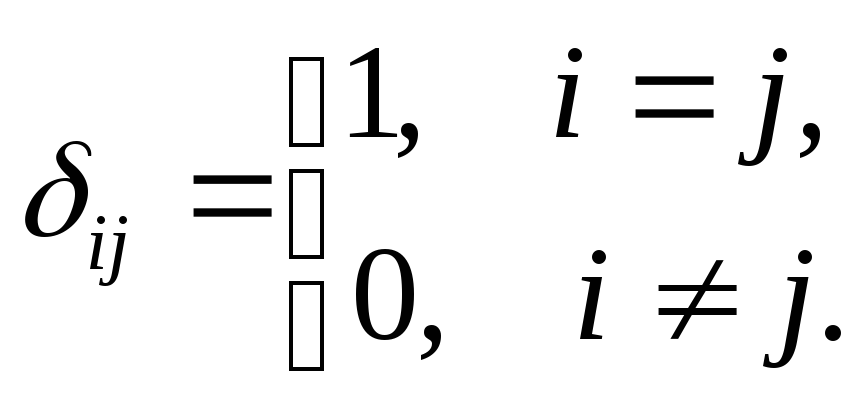
Так если ввести новые обозначения для базисных векторов , то условие ортонормированности базиса запишется в виде

.

Если к этому переобозначить компоненты вектора , то разложение вектора по базису примет вид

.

Можно и эту запись упростить, если договорится, что по повторяющимся индексам подразумевается суммирование (если это не противоречит сути формулы)

.

В новых обозначениях скалярное произведение векторов запишется в виде

.

Заметим, что в силу своего определения символ Кронекера «снимает» сумму, например, .

Символ Леви-Чивита имеет три индекса и обозначается через , при этом полагается, по определению, что . Этот символ является полностью антисимметричным, т.е. при перестановке местами любых двух индексов он меняет знак, например, . Используя это свойство, можно найти значения этого символа при любых индексах, не равных друг другу (). Условие антисимметричности символа Леви-Чивита также приводит к результату: если какие-либо два индекса равны у этого символа, то он равен нулю, например, .

С помощью символа Леви-Чивита -ая координата векторного произведения векторов и представима в виде

,

где, как говорилось выше, по индексам и берется двойная сумма. Например,

, т.е. .

Смешанное произведение векторов вычисляется по формуле

.

Заметим, что повторяющиеся индексы, по которым проводится суммирование, называются связанными индексами, а индексы, по которым не проводится суммирование, - свободными индексами. В начале расчета и в его конце свободные индексы должны совпадать. При вычислениях полезны формулы

,

.

Если встречается двойная сумма , где объект симметричный по индексам , а объект антисимметричный , то указанная выше сумма равна нулю. Рассмотрим пример расчета с помощью введенных символов.

Пример. Показать, что .

.

Замечание. Определитель третьего порядка также можно записать через символ Леви-Чивита

.

ЗАДАЧИ