m_ukazanija__01
.doc
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
_
Кафедра высшей математики
векторная алгебра и аналитическая геометрия
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ И
ВЫПОЛНЕНИЮ РАСЧЕТНОГО ЗАДАНИЯ
ДЛЯ СТУДЕНТОВ ЗАОЧНОГО ОТДЕЛЕНИЯ
Москва 2007
С о с т а в и т е л и:
доцент, кандидат физико-математических наукТ.А.Мацеевич
Примеры решения задач по векторной алгебре и аналитической геометрии
Задание №1
Разложить вектор
=
{9, 4} по векторам
=
{2, -3} и
=
{1, 2}.
Решение.
Найдем коэффициенты
и
в разложении:
=
+
.
Запишем эту формулу в координатах. Сначала вычислим координаты правой части:
+
=
{2
;
-3
}
+ {1
;
2
}
= {2
+
;
-3
+ 2
}.
Эти координаты должны равняться
соответствующим координатам вектора
,
следовательно:
.
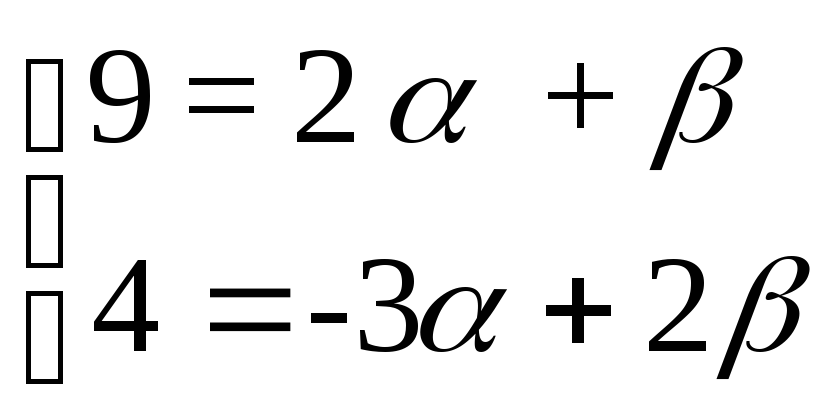Решим эту систему уравнений методом исключения переменных.
Ответ:
= 2
+ 5
.
Задание №2
Проверить коллинеарность векторов
=
{2, -1, 3} и
=
{-6, 3, -9}.
Решение.
Если векторы
и
коллинеарны,
то их координаты должны быть пропорциональны.
Проверим это.
,
т.е коэффициент пропорциональности
существует и равен
.
Ответ:
II
.
Задание №3
Дан вектор
=
{2, -1, 3}. Найти модуль вектора
,
координаты его орта
и направляющие косинусы.
Решение.
а) Найдем модуль вектора
:
.
б) Найдем координаты орта
:
=
.
в) Найдем направляющие косинусы вектора
:
;
;
.
Ответ:
,
,
,
,
.
Задание №4
Проверить ортогональность векторов
=
{-6, -3, 2} и
=
{1, 2, 6}.
Решение.
Если
,
то их скалярное произведение
.
Найдем
.
.
Ответ:
.
Задание №5
Найти угол между векторами
=
{3, 0, 4} и
=
{7, 0, 1}.
Решение.
Пусть
- угол между векторами
и
.
Тогда
.
Найдем скалярное произведение:
.
Найдем модули векторов
и
:
;
.
Найдем
:
.
Тогда
.
Ответ:
.
Задание №6
Найти вектор
,
перпендикулярный векторам
=
{2, -2, -3} и
=
{4, 0, 6}.
Решение.
Так как
и
,
то
(векторное
произведение векторов
и
).
{-12,
-24, 8}.
Ответ:
{-12,
-24, 8}.
Задание №7
Вычислить площадь параллелограмма ABDC и треугольника ABC, если А(0, 2, 2), B(1, -2, 3), C(-1, 2, 1), D(0, -2, 2).
Решение.
Найдем векторы
и
:
=
{ 1, -4, 1},
=
{-1, 0, -1}.
Найдем векторное произведение полученных векторов:
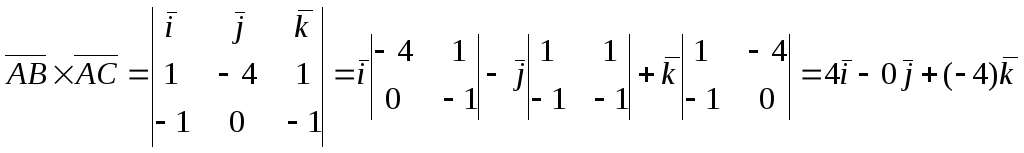={4,
0, -4}.
Найдем длину полученного вектора
.
Найдем площадь параллелограмма ABDC:
.
Найдем площадь треугольника ABC:
.
Ответ:
,
.
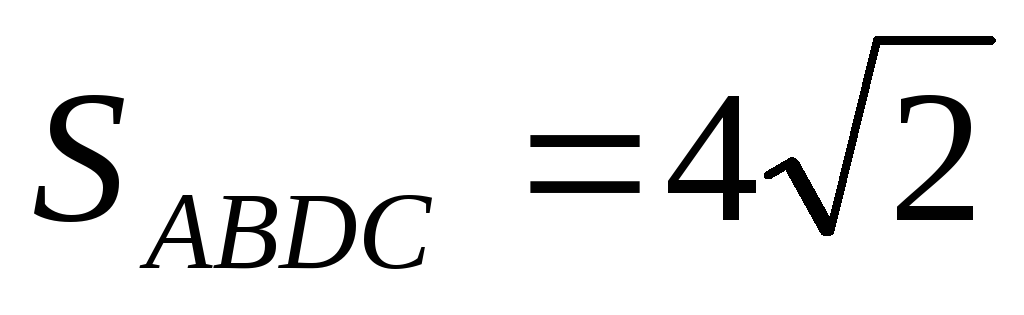Задание №8
Найти объем пирамиды, вершины которой находятся в точках A(2, -1, 1), B(5, 5 , 4),
C(3, 2, -1), D(4, 1, 3).
Решение.
Найдем координаты векторов
,
,
:
{3,
6, 3},
=
{1, 3, -2},
=
{2, 2, 2}.
Вычислим смешанное произведение этих векторов:
Найдем объем пирамиды:
.
Ответ:
.
Задание №9
Проверить компланарность векторов
=
{2, 3, -1},
=
{1, -1, 3} и
=
{1, 9, -11}.
Решение.
Вычислим смешанное произведение векторов
,
и
:
Так как
,
следовательно, векторы
,
и
- компланарны.
Ответ:
,
и
- компланарны.
Задание №10
Составить общее уравнение прямой,
проходящей через точки
(3;
1) и
(5;
4).
Решение.
Подставляя данные координаты точек
и
в формулу
,
получаем искомое уравнение прямой
,
,
,
.
Ответ:
.
Задание №11
Две прямые заданы уравнениями
и
.
Найти угол между этими прямыми.
Решение.
Угловые коэффициенты данных прямых:
.
Поэтому по формуле
,
находим
.
Таким образом, угол между данными прямыми равен
.
Ответ:
.
Задание №12
Показать, что прямые
и
параллельны.
Решение.
При приведении уравнения каждой прямой к виду
получаем:
или
;
и
или
.
Откуда видно, что угловые коэффициенты
.
Следовательно, прямые параллельны.
Ответ: т.к.
,
данные прямые параллельны.
Задание №13
Показать, что прямые
и
перпендикулярны.
Решение.
Приведя уравнения каждой прямой к виду
получаем:
или
,
где
- угловой коэффициент,
и
или
,
где
- угловой коэффициент.
Откуда видно, что угловые коэффициенты
.
Следовательно, прямые перпендикулярны.
Ответ: т.к.
,
данные прямые перпендикулярны.
Задание №14
Составить уравнение плоскости проходящей
через точку
(1;
1; 1) перпендикулярно вектору
{2;
2; 3}.
Решение.
По формуле
,
где
-
координаты точки, лежащей в плоскости,
а
-
координаты вектора, перпендикулярного
данной плоскости, искомое уравнение
будет:
,
.
Ответ:
.
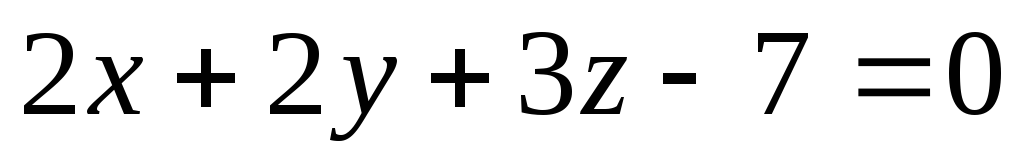Задание №15
Найти каноническое уравнение прямой заданной пересечением плоскостей:
.
Решение.
Полагая, например,
,
из системы
или
получаем
и
Таким образом, точка
(1;
2; 1) искомой прямой найдена.
Теперь определим направляющий вектор
.
Так как прямая определена пересечением
плоскостей, то она перпендикулярна
каждому из нормальных векторов
и
.
Поэтому, в качестве вектора
можно взять любой вектор, перпендикулярный
векторам
и
,
например их векторное произведение
.
Так как координаты векторов известны:
= {3; 2; 4}
= {2; 1; -3},
то
{-10;
17; -1}
или
= -10,
=
17,
=
-1.
Подставляя найденные значения
,
,
и
,
,
в равенства:
,
получаем каноническое уравнение данной прямой:
.
Ответ:
.
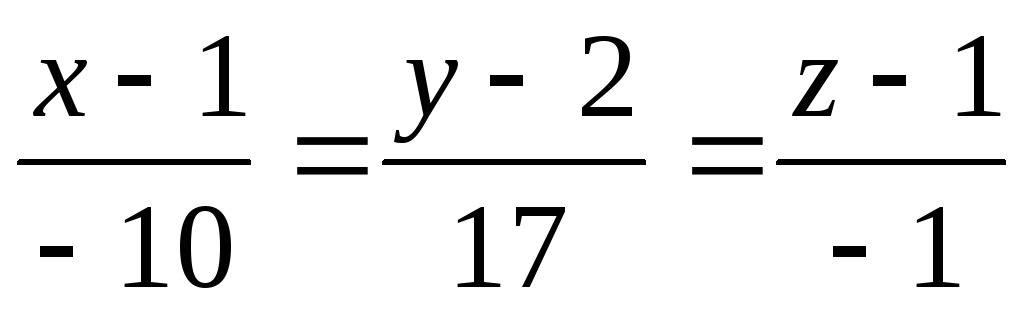Задание №16
Найти точку пересечения прямой
с плоскостью
.
Решение.
Параметрические уравнения прямой имеют вид
,
,
.
Для определения точки пересечения прямой и плоскости подставим выражения для x, y, z из уравнения в уравнение плоскости. Получаем
,
,
откуда находим
.
Следовательно, координаты точки пересечения будут:
,
,
.
Итак, прямая и плоскость пересекаются
в точке
(
;
;
).
Ответ: точка
пересечения
(
;
;
).
Задание №17
Дана система линейных уравнений:
Решить эту систему:
а) по формулам Крамера,
б) с помощью обратной матрицы.
Решение.
а) Найдем определитель, состоящий из коэффициентов перед переменными:
Посчитаем определитель, у которого 1-ый столбец заменяется столбцом свободных членов:
.
Посчитаем определитель, у которого 2-ой столбец заменяется столбцом свободных членов:
.
Посчитаем определитель, у которого 3-ой столбец заменяется столбцом свободных членов:
.
Найдем значения x, y и z по формулам Крамера:
;
;
.
Ответ:
,
,
.
б) Рассмотрим матрицы:
-
матрица, состоящая из коэффициентов
перед переменными;
-
матрица, состоящая из свободных членов;
-
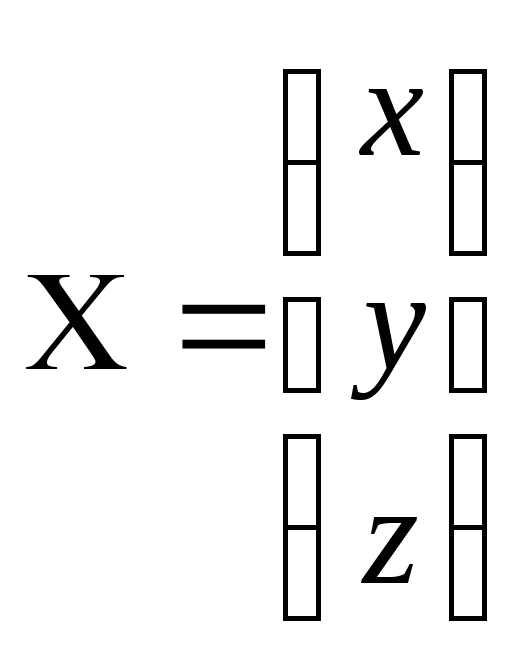матрица, состоящая из неизвестных.
Тогда, в матричной форме система линейных уравнений может быть записана следующим образом:
.
Если
,
то система имеет единственное решение,
которое можно найти по формуле:
,
где
- обратная матрица к матрице
.
Найдем
.
.
Найдем определитель матрицы A:
обратная матрица существует.
Определим алгебраические дополнения
:
; 
; 
;
; 
; 
;
; 
; 
.
Посчитаем
:
.
Найдем
:
.
,
,
.