2. Сложное сопротивление стержней.

Основные понятия и формулы

Сложное сопротивление в стержне имеет место при действии на него произвольных нагрузок, которые можно разложить на осевые, поперечные и скручивающие составляющие.

В общем случае сложного сопротивления в поперечных сечениях стержня действуют нормальные напряжения _х и касательные напряжения _ух и _zx , равнодействующими которых являются шесть внутренних усилий – продольная сила N , изгибающие моменты M_z и M_y , поперечные силы Q_z и Q_y и крутящий момент M_x = M_к (рис.2.1).

Рис.2.1

Нормальные напряжения в поперечном сечении при наличии всех трёх их равнодействующих N , M_z и M_y определяются по формуле

. (2.1)

Плоский косой изгиб имеет место, когда все поперечные нагрузки действуют в плоскости, не совпадающей с главными плоскостями инерции (рис.2.2).

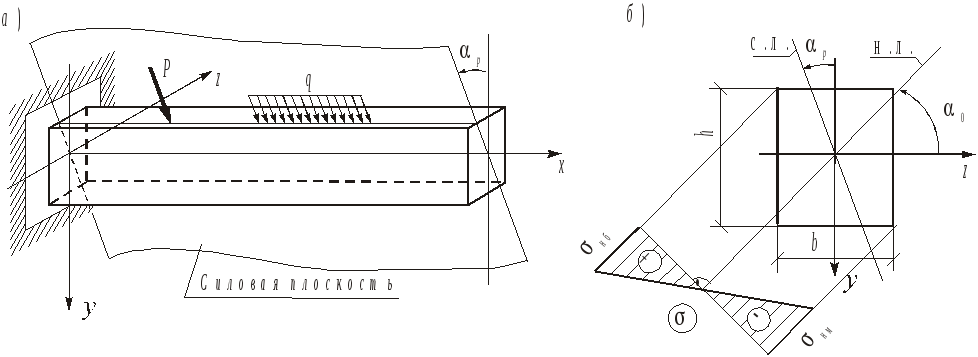
Рис.2.2

Пространственный косой изгиб имеет место при действии поперечных нагрузок в различных плоскостях (рис.2.3).

Н ормальные напряжения в поперечном сечении определяются по формуле

(2.2)

и

Рис.2.3

згибающие моменты M_z и M_y в случае плоского косого изгиба определяются по формулам

М_z = Mcos_P , М_y = Msin_P , (2.3)

где М – суммарный изгибающий момент, действующий в силовой плоскости (рис.2.2).

При пространственном косом изгибе М_zиМ_yвычисляются раздельно от нагрузок в главных плоскостях и в общем случае изменяются по различным законам, а их отношение не является постоянной величиной.

Приравнивая выражение (2.2) к нулю, получим уравнение нулевой линии

. (2.4)

Угол наклона нулевой линии ₀связан с углом наклона силовой линии_Р (рис.2.2) формулой

. (2.5)

Условие прочности при косом изгибе для балок с поперечным сечением типа прямоугольника или двутавра записывается в виде

. (2.6)

В случае пространственного косого изгиба изгибающие моменты М_z и М_у могут иметь наибольшие значения в различных сечениях, поэтому условие прочности (2.6) необходимо проверять, по крайней мере, в сечениях, где один из моментов имеет наибольшее значение.

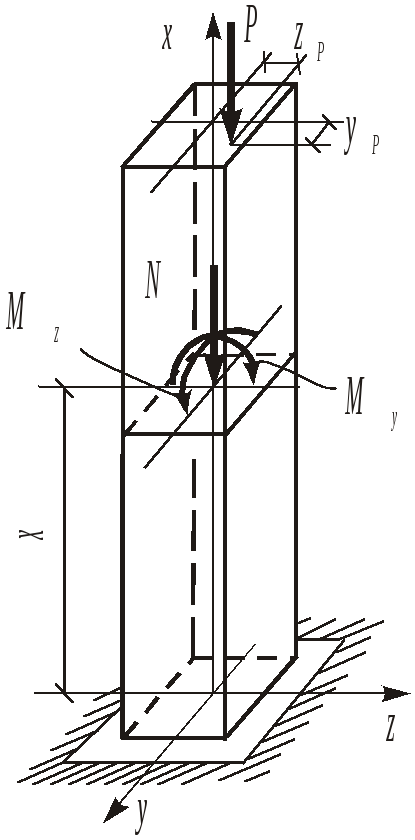
Внецентренное растяжение и сжатие имеет место в случае, когда нагрузки действуют вдоль прямой, параллельной оси стержня. При внецентренном сжатии внутренние усилия в поперечном сечении стержня равны

N = – P , M_z = – P y_P M_y = – P z_P , (2.7)

где у_Р,z_P– координаты точки приложения силы.

Напряжения определяются по формуле (2.1), которая с учётом (2.7) принимает вид

, (2.8)

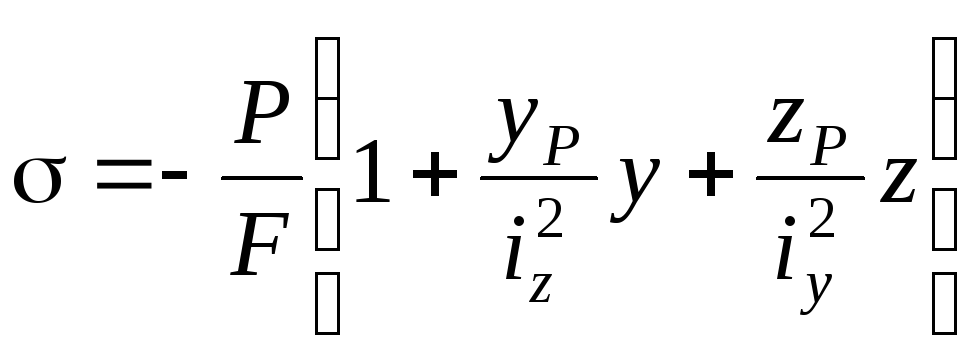
где величины

, (2.9)

называются главными радиусами инерции сечения.

Уравнение нулевой линии имеет вид

. (2.10)

Отрезки, отсекаемые нулевой линией на осях координат, определяются по формулам

Рис.2.4

, , (2.11)

Если материал стержня неодинаково сопротивляется растяжению и сжатию, то необходимо обеспечить выполнение двух условий прочности

(2.12)

где R_р и R_с – расчётные сопротивления материала при растяжении и сжатии, z_A, у_А и z_B, у_В – координаты наиболее напряжённых точек сечения.

Ядро сечения – это выпуклая область, содержащая центр тяжести сечения и обладающая тем свойством, что при нахождении точки приложения силы внутри этой области или на её границе во всех точках сечения напряжения имеют одинаковый знак. Координаты точек контура ядра сечения определяются с помощью формул (2.11).

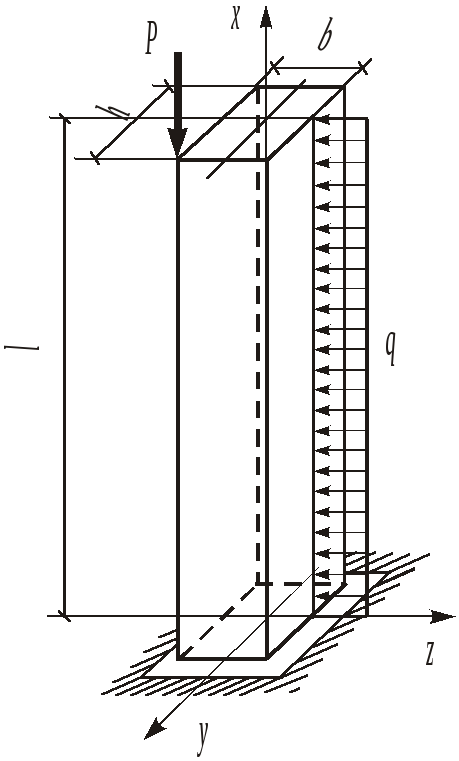
Растяжение и сжатие с изгибом имеет место при одновременном действии на стержень продольных и поперечных нагрузок (рис.2.5). Нормальные напряжения в поперечных сечениях определяются по общей формуле (2.1). Приравняв это выражение к нулю, получим уравнение нулевой линии

. (2.13)

Положив в этом уравнении последовательно у = 0 и z = 0 , получим

формулы для определения отрезков, отсекаемых нулевой линией на осях координат:

. (2.14)

Наибольшие растягивающие и сжимающие напряжения действуют в точках сечения, наиболее удалённых от нулевой линии. Значения этих напряжений для поперечных сечений типа прямоугольника и двутавра можно определить по формулам

, . (2.15)

Рис.2.5

Изгиб с кручением имеет место в случае, если стержень подвергается одновременному действию поперечных и скручивающих нагрузок.

Нормальные напряжения, вызываемые изгибом стержня, определяются по формуле (2.2), а касательные – по формуле Д.И.Журавского. Касательные напряжения, вызываемые кручением стержня, зависят от величины крутящего момента.

При изгибе с кручением расчет стержней на прочность необходимо производить с использованием теорий прочности. Рассмотрим наиболее часто используемые при практических расчётах теории прочности и выпишем соответствующие этим теориям условия прочности для стержней.

• теория наибольших касательных напряжений:

. (2.16)

• энергетическая теория прочности:

. (2.17)

Теория наибольших касательных напряжений и энергетическая теория хорошо подтверждаются экспериментально для пластичных материалов.