
Примеры расчета рамных конструкций 2013
.pdf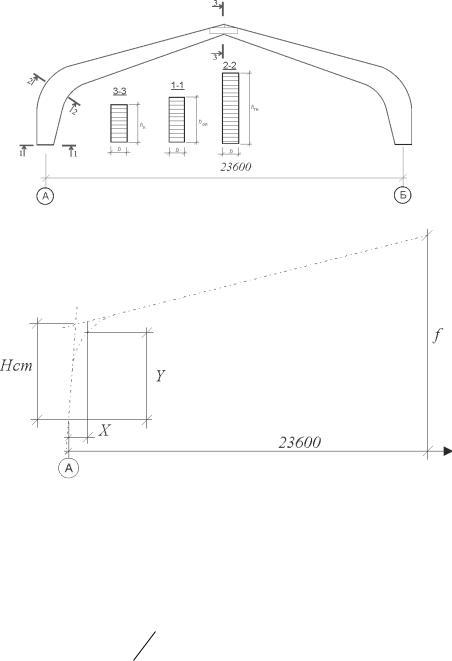
Рис. 7. Гнутоклееная рама
Рис. 8. Изогнутая ось гнутоклееной рамы
Расчетный пролет рамы lр = 23,6 м. Расчетный пролет принимается между осями, т.е., пролет рамы уменьшается на 0,4 м. Уклон ригеля
1:4, т.е. tgα = 1/4 = 0,25; угол наклона ригеля α = 14 02 ; sin α = 0,24; cos α = 0,97. Высота рамы в коньке (высота по оси рамы) f = 6,95 м. Тогда высота стойки от верха фундамента до точки пересечения касательных по осям стойки и ригеля:
Н f lp |
2 |
tg( ) 6,95 11,8 0,25 4 м. |
|
|
|
|
|
21 |
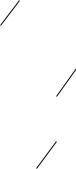
По условиям гнутья, толщина досок после фрезерования должна приниматься не более 1,6…2,5 см. Принимаем доски толщиной 2,5 см, после фрезеровки 1,9 см. Радиус гнутой части принимаем равным
r = 3 м > rmin = 150ºδ = 150 0,019 = 2,85 м (где δ — толщина склеи-
ваемых досок).
Угол в карнизной гнутой части между осями ригеля и стойки:
γ 90o α 90o 14o02 104o02 .
Так как максимальный изгибающий момент — в среднем сечении гнутой части рамы, которое находится на биссектрисе этого угла, получим:
(90 α) / 2 (90 14 02 ) / 2 52 01 ; sinβ 0,788; cosβ 0,62; tgβ 1,28.
Центральный угол гнутой части рамы в градусах и радианах:
φ(90 β)2 (90 52o 01 )2 37o 59 2 75o 58 , или φ 90 α 90o 14o 02 75o 58 ;
φрад πφ /180o 3,14 75o 58 /180o 1,33;
φ1 φ 2 37o 59 ; sinφ1 0,615; cosφ1 0,788, tgφ1 0,78.
Длина гнутой части lгн = rφрад = 3 1,33 = 3,99 м. Длина стойки от опоры до начала гнутой части:
lст f lр 2 tgα r cosα r (1 sinα) tgα
= 6,95 11,8 0,25 3 0,97 + 3(1 0,24)0,25 = 1,66 м.
Длину стойки можно определить иначе (если известно f):
lст f lр 2 tgα r tgφ1 6,95 11,8 0,25 3 0,78 1,66 м.
Длина прямолинейной части ригеля:
lриг = (lр / 2 – r + r sin ) / cos = (11,8 – 3 + 3 0,24) / 0,97 = 9,8 м.
Длина полурамы:
lпр = lст + lгн + lриг = 1,66 + 3,99 + 9,8 = 15,45 м.
3.1.3. Определение нагрузок на раму
Нагрузки от покрытия (постоянные нагрузки) принимаем по предварительно выполненным расчетам ограждающих конструкций. В нашем примере:
22
qн 0,43 кH/м2 ; |
qр 0,499 кH/м2 . |
Собственный вес рамы определяем при ксв = 6 из выражения:
|
|
qн S н |
0,43 0,84 |
|
||||||
qн |
|
|
|
|
|
|
|
|
|
0,209 кH/м2 , |
|
|
|
|
|
|
|
||||
св |
|
1000 |
|
|
1000 |
|
|
|||
|
|
1 |
1 |
|
||||||
|
|
к |
св |
l |
|
6 23,6 |
|
|||
|
|
|
|
|
|
|
||||
|
|
|
р |
|
|
|
|
|
|
|
где Sн — нормативная снеговая нагрузка для г. Белгорода, lр — расчетный пролет;
ксв — коэффициент собственного веса рамы, принимаемый по табл. 7.3 [7]. ксв = (5–9) при пролетах рам (15–30 м).
Порядок определения временных нагрузок
1. Снеговая нагрузка принимается в соответствии со сводом правил СП 20.13330.2011 по СНиП 2.01.07-85* (актуализированная редакция). Нормативное значение снеговой нагрузки на горизонтальную проекцию покрытия для г. Белгорода следует определять по формуле:
S о = 0,7∙C е ∙ C t ∙ µ ∙ S g ,
где C e — коэффициент, учитывающий снос снега с покрытий зданий под действием ветра или иных факторов, принимаемый в соответствии с 10,5; для покрытий с уклоном кровли для однопролетных
и двухпролетных зданий от 12–20 %, т.е α 7 12,5o C e = 0,85. В
нашем примере α = 14 02 ; следовательно, C e = 1,0.
C t = 1,0 — термический коэффициент, принимаемый в соответствии с 10,6;
µ= 1 — коэффициент перехода от веса снегового покрова земли
кснеговой нагрузке на покрытие, принимаемый в соответствии с
10,4;
Sg = 1,2 кПа — вес снегового покрова на 1 м2 горизонтальной поверхности земли, принимаемый в соответствии с 10.2.
Sо = 0,7·1,0·1,0 1·1,2 = 0,84 кПа.
Расчетная снеговая Sр= Sо·γ,
где γ =1,4 — коэффициент надежности по снеговой нагрузке.
Sр = 0,84·1,4 = 1,176 кПа.
В табл. 2 представлены значения погонных нагрузок, действующих на раму (при шаге рам 3 м).
23
Т а б л и ц а 2
Значения погонных нагрузок, действующих на раму
|
Нормативное |
Коэффициент |
Расчетное значение |
|
Вид нагрузки |
значение |
надежности |
||
нагрузки, кН/м |
||||
|
нагрузки, кН/м |
по нагрузке |
||
|
|
|||
Собственный вес |
0,43∙3 / cosα = |
— |
0,499∙3 / cosα = |
|
покрытия |
= 1,29/0,97 = 1,33 |
|
1,5/0,97 = 1,54 |
|
Собственный вес рамы |
0,209∙3 = 0,627 |
1,1 |
0,69 |
|
И т о г о: |
1,96 |
— |
2,23 |
|
Снеговая нагрузка |
0,84∙3 = 2,52 |
— |
1,176∙3 = 3,53 |
|
В с е г о: |
1,96 + 2,52 = 4,48 |
— |
2,23 + 3,53 = 5,76 |
3.1.4. Статический расчет рамы
Максимальные усилия в гнутой части рамы возникают при действии равномерно распределенной нагрузки q = 5,76 кН/м по пролету (см. табл. 2 сбора нагрузок). Опорные реакции:
а) вертикальные:
A B |
q l |
р |
|
5,76 23,6 |
67,97 кН; |
|
|
|
|||
2 |
|
2 |
|||
|
|
|
|
б) горизонтальные (распор):
|
q lр2 |
5,76 23,62 |
|||
Н |
|
|
|
|
57,7 кН, |
|
|
|
|||
|
8 |
f |
8 6,95 |
||
где lр — расчетный пролет рамы;
f — стрела подъема рамы (высота рамы в коньке).
Максимальный изгибающий момент в раме возникает в центральном сечении 2-2 гнутой части (cм. рис. 7—8). Координаты этой точки можно определить из следующих соотношений:
хr (1 cosφ1) 3 (1 0,788) 0,636 м,
уlст r sinφ1 1,66 3 0,615 3,505 м.
Определяем М и N в этом сечении:
М Ах |
qx2 |
Hy; |
|
|
|
|
|||
2 |
|
|
|
|
М 67,97 0,636 |
5,76 0,6362 |
57,7 3,505 160,17 кН×м |
||
|
||||
2
N (A qx)sin β H cosβ;
N ( 67,97 5,76 0,636 ) 0,79 57,7 0,62 86,576 кH.
24
3.1.5.Подбор сечения и проверка напряжений
Всечении 2–2 (рис. 7) максимальный момент Мmах = 160,17 кH м, продольная сила N = 86,576 кН. Расчетное сопротивление сжатию и изгибу для сосны II сорта при ширине b = 14 см (принимаем доски шириной b = 15 см до фрезерования):
Rc 15 mв 15 1 15,8 МПа 1,58 кН / см2 , γн 0,95
где 15 МПа — расчетное сопротивление сжатию древесины сосны II сорта (по табл. 3 [5]),
m в — коэффициент условий эксплуатации (табл. 7 [5]), γн — коэффициент надежности.
Можно принять ширину сечения рамы b = 16 cм из досок шириной 17,5 см до фрезерования, b = 18 cм, из досок шириной b = 20 см. Если необходимо принять сечение большей ширины, то необходимо использовать составное сечение по ширине 22 см из досок b = (15 + 10) см, b = 24 см из досок (17,5 + 10) см, b = 27 см, из досок b = (17,5 + 12,5) см до фрезерования.
Требуемую высоту сечения hтр можно определить приближенно по величине изгибающего момента, а наличие продольной силы учесть введением коэффициента 0,6:
|
|
|
|
|
|
6 160,17 10 3 |
|
|
|
hтр |
6М |
(0,6bRc ) |
|
(0,6 0,14 15,8) |
0,851 м. |
||||
|
|
||||||||
|
|
|
|
|
|
|
|||
Требуемое |
|
|
количество |
слоев |
равно: |
||||
nтр hтр |
: δсл 0,851 : 0,019 44,8 слоев 45 слоев. |
|
|||||||
Принимаем высоту сечения несколько больше (на 5—7 слоев) требуемой, при этом высота сечения должна состоять из целого числа досок, т.е. принимаем 52 слоя толщиной после фрезерования δ =
19 мм, тогда hгн = 52 19 = 988 мм > 851 мм.
Высоту сечения ригеля в коньке рамы принимаем 0,3 hгн, т.е. hк = 18 19 = 342 мм > 0,3hгн = 0,3 988 = 296 мм.
Высоту сечения опоры рамы hоп ≥ 0,4hгн принимаем hоп = 23 19 = = 437 мм > 0,4 hгн = 0,4 988 = 380 мм, что позволит не выполнять дополнительных проверок.
Геометрические характеристики принятого сечения:
25

F |
b h |
0,14 0,988 138,32 10 3 м2 ; |
|||
|
расч |
гн |
|
|
|
W |
b h |
2 |
/ 6 0,14 0,9882 |
/ 6 22,78 10 3 м3 ; |
|
|
расч |
гн |
|
|
|
J |
расч |
b h |
3 |
/ 12 0,14 0,9883 |
/ 12 11,25 10 3 м4 . |
|
гн |
|
|
|
|
Коэффициенты условий работы к расчетным сопротивлениям принимаем mв = 1 по табл. 7 [5]; коэффициент mб для высоты сечения 98,8 см по интерполяции значений табл. 9 [5]:
mб 0,9 0,9 0,85 18,8 0,853 ; 20
mсл = 1,1 по табл. 10 [5].
Радиус кривизны в гнутой части по нейтральной оси
|
r0 r z r |
hгн |
3 |
0,988 |
2,973м . |
|||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
12 r |
|
12 3 |
||||
Отношение |
|
r0 |
|
2,973 |
156,47 , тогда по интерполяции значений |
|||||||||
|
|
|
|
|
|
|||||||||
|
|
δсл |
0,019 |
|
|
|
|
|
|
|
||||
табл. 11 [5] находим коэффициент mгн: |
||||||||||||||
mгн 0,8 |
0,9 0,8 |
6,47 0,813 (для Rc и Rи); |
||||||||||||
|
|
|||||||||||||
|
|
|
|
50 |
|
|
|
|
|
|
||||
|
|
mгн |
0,6 |
0,7 0,6 |
|
6,47 0,613 (для Rр). |
||||||||
|
|
|
||||||||||||
|
|
|
|
50 |
|
|
|
|
|
|||||
3.1.6. Проверка напряжений при сжатии с изгибом
Для криволинейного участка рамы отношение hгн/r = 0,988/3,0 = = 1/3,04 > 1/7.
Изгибающий момент, действующий в биссектрисном сечении 2–2 (см. рис. 7 и 8) находится на расстоянии от расчетной оси, равном:
е = (hгн – hоп) / 2 = (0,988 – 0,437) / 2 = 0,2755 м.
Расчетное сопротивление древесины сосны II сорта:
сжатию и изгибу:
Rc = Rи = 15 mв mб mсл mгн γН /γn = 15 1 0,853 1,1 0,813∙1/0,95 = = 12,04 МПа,
где 15 МПа — расчетное сопротивление сосны II сорта — см. табл. 3
СП [5];
растяжению:
Rр = 9 mв mгн γН /γn = 9 1 0,613 1/ 0,95 = 5,807 МПа,
где 9 МПа — расчетное сопротивление по табл. 3 СП [5].
26

Расчетная длина полурамы по осевой линии равна lпр = 15,45 м (подсчитано выше), радиус инерции сечения r = 0,289∙0,988 = 0,285532 м, тогда гибкость λ = lпр /r = 15,45 / 0,285532 = 54,1.
Для элементов переменного по высоте сечения коэффициент φ следует умножить на коэффициент кжN, принимаемый по табл. Е.1 прил. Е СП [5].
кжN = 0,66 + 0,34β = 0,66 + 0,34∙0,437 / 0,988 = 0,81, где β hоп hгн 0,4370,988;
φ 3000λ2 300054,12 1,025 ,
если произведение kжN 1, то принимаем kжN = 1, в нашем слу-
чае имеем kжN = 1,025 0,81 = 0,83.
Изгибающий момент, определяемый с учетом дополнительного момента от продольной силы по деформированной схеме:
|
Мд = M / ξ = 160,17 / 0,958 = 167,19 кН м, |
|||
где ξ 1 |
N0 |
1 |
57,7 10 3 |
0,958, |
φ R F |
0,83 12,04 138,32 10 3 |
|||
|
c расч |
|
|
|
где N0 — усилие в коньковом шарнире; N0 = H = 57,7 кН; Rc = 12,04 МПа.
Для криволинейного участка при отношении h/r = 0,988 / 3,0 = 1/3,04 > 1/7 согласно [2, 3] прочность следует проверять для наружной и внутренней кромок, вводя коэффициенты кrвн и кrнар к Wрасч:
|
|
1 0,5 h |
|
|
|
|
|
1 0,5 0,988 |
|
|
|
|||||
кr вн |
r |
|
|
|
|
|
3,0 |
|
0,8353 |
0,885; |
||||||
|
|
hr |
1 0,17 0,988 |
|||||||||||||
|
|
1 0,17 |
|
|
|
0,944 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3,0 |
|
|
|
|
|
|
|
1 0,5 h |
|
|
|
|
|
1 0,5 0,988 |
|
|
|
||||
кr нар |
|
r |
|
|
|
3,0 |
1,1647 |
1,086. |
||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
1 0,17 hr |
1 0,17 |
0,988 |
|
1,056 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3,0 |
|
|
||
Расчетный момент сопротивления с учетом влияния кривизны
Wв Wрасч кrвн 22,78 10 3 0,885 20,16 10 3 м3 ; Wн Wрасч кrнар 22,78 10 3 1,086 24,74 10 3 м3 .
Напряжение по сжатой внутренней кромке
σс N Fнт Мд Wв Rс ;
27

σc 86,576 103 167,19 10 3 8,92 МПа Rc 12,04 МПа. 138,32 10 3 20,16 10 3
Напряжение по растянутой наружной кромке
σ |
р |
Мд |
Wн |
N |
R ; |
(5) |
|
|
|
р |
|
||
|
|
|
|
Fнт |
|
σр 167,19 10 3 86,576 10 3 6,132 МПа Rр 5,807 МПа. 24,74 10 3 138,32 10 3
Это означает, что условие прочности по растяжению не удовлетворяется. Необходимо увеличить высоту сечения и провести проверку по формуле (5).
Добавим еще один слой по 1,9 см, тогда высота гнутой части рассчитывается по следующей формуле:
h |
0,988 0,019 |
1,007 м; |
|
||||||
гн |
|
|
|
|
|
|
|
|
|
F 1,007 0,14 140,98 10 3 м2; |
|
||||||||
W |
|
|
b h2 |
/ 6 0,14 1,0072 / 6 |
23,66 10 3 м3; |
||||
расч |
|
гн |
|
|
|
|
|
||
|
|
|
|
1 0,5 1,007 |
|
|
|
|
|
kгнар |
|
3,0 |
1,105; |
|
|||||
|
|
|
|||||||
|
|
|
1 0,17 1,007 |
|
|
|
|
||
|
|
|
|
|
3,0 |
|
|
|
|
σр |
|
|
|
167,19 10 3 |
|
|
86,576 10 3 |
5,781 МПа Rр 5,807 МПа. |
|
|
|
|
|
|
|
||||
|
|
23,66 10 3 1,105 140,98 10 3 |
|
||||||
Недонапряжение по одной из проверок должно быть меньше 5%. В нашем случае недонапряжение составляет
5, 781 5,807 100% 0, 45% 5% , условие прочности выполняется.
5,807
Окончательно принимаем сечения рамы:
hгн = 100,7 см; hк = 34,2 см; hоп = 43,7 см; где hк = 18 1,9 = 34,2 см > 0,3 100,7 = 30,21 см;
hоп = 23 1,9 = 43,7 см > 0,4 100,7 = 40,28 см.
3.1.7. Проверка устойчивости плоской формы деформирования рамы
Рама закреплена из плоскости:
в покрытии по наружной кромке прогонами (или плитами) по ригелю;
по наружной кромке стойки стеновыми панелями.
28
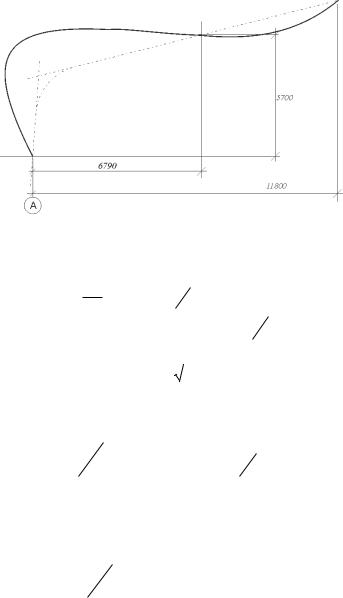
Внутренняя кромка рамы не закреплена. Эпюра моментов в раме имеет вид, представленный на рис. 9.
Рис. 9. Эпюра изгибающих моментов
Точку перегиба моментов, т.е. координаты точки с нулевым мо-
ментом, находим из уравнения моментов (4), приравнивая его к нулю:
М Ах qx22 H (f tgα( l 2 х)) 0;
67,97 х 5,76х2 57,7((6,95 0,25(23,62 х)) 0; 2
2,88х2 –53,545х+230,8 =0, получаем уравнение вида ах2+вх + с = 0;
х |
|
в |
|
в2 4ас |
. |
|
|
|
|||
1,2 |
|
|
2а |
|
|
|
|
|
|
||
Решая уравнение, получим х1=11,80; х2=6,79; принимаем х2 =6,79 м, тогда
l |
р |
|
|
|
|
|
|
6,95 0,25 (23,6 |
|
6,79) 5,7 м. |
|
у f tgα |
х |
2 |
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Точка перегиба эпюры моментов соответствует координатам х = 6,79 м от оси опоры, у = 5,7 м.
Тогда расчетная длина растянутой зоны, имеющей закрепления по наружной кромке, равна:
|
|
|
|
|
|
lр |
х |
1,66 3,99 9,8 11,8 6,79 10,28 м. |
l |
р1 |
l |
l |
l |
|
2 |
||
|
|
|||||||
|
ст |
гн |
риг |
|
соsα |
0,97 |
||
|
|
|
|
|
|
|||
29

Расчетная длина сжатой зоны, наружной (раскрепленной) кромки ригеля (т.е. закреплений по растянутой кромке нет) равна
l |
l |
2 |
х |
11,8 6,79 |
5,16 м. |
|
|
|
|||||
cosα |
||||||
р2 |
0,97 |
|
||||
|
|
|
|
|
||
Таким образом, проверку устойчивости плоской формы деформирования производим для двух участков.
Проверка устойчивости производится по формуле (38) п. 6.20 СП
[5]. |
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
M |
д |
n |
|
|
|
|
|
|
|
1, |
(6) |
|||
|
φ R F |
φ |
|
R W |
|||||
|
|
м |
|
|
|||||
|
у c бр |
|
|
и |
бр |
|
|
||
Проверка устойчивости плоской формы деформирования рамы проводится на двух участках lр2 и lр1:
1. Для участка lр2 = 5,16 м находим максимальную высоту сече-
ния в месте максимального момента из соотношения |
|
|||||||||||||||||
h' h |
h |
гн |
hк lр2 |
/ 2 |
0,342 |
|
1,007 0,342 5,16 / 2 |
0,517 м; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
к |
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
9,80 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
риг |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λу lр2 |
|
|
|
|
5,16 |
|
|
|
127,53; |
|
|||||
|
|
|
|
|
0,289 b |
|
|
|
0,289 0,14 |
|
|
|||||||
|
|
|
φу |
3000 |
|
3000 |
|
0,184; |
|
|||||||||
|
|
|
|
|
|
|
|
λ2у |
|
|
|
|
|
127,532 |
|
|
|
|
|
φ |
140 |
|
b2 |
|
|
k |
140 |
|
0,142 |
|
1,13 1,162, |
||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
м |
|
lр2 h1 |
ф |
|
|
|
|
|
5,16 0,517 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
где Кф см. табл. Е. 2 прил. Е. СП [5]; |
|
|
|
|
||||||||||||||
|
|
|
F 0,517 0,14 72,4 10 3 |
м2 ; |
|
|||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
0,14 0,5172 |
6,24 10 3 м3 . |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
|
|
6 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Показатель степени n = 2, так как на данном участке нет закреплений растянутой зоны.
Находим максимальный момент и соответствующую продольную силу на расчетной длине 5,16 м, при этом горизонтальная проекция этой длины будет равна
l1р2 lр2 cosα 5,16 0,97 5,005 м.
30
