19. Оптимизация запуска изделий в производство

Постановка задачи. Необходимо спланировать производство (ремонт, обслуживание) нескольких видов изделий, каждое из которых должно быть обработано на двух видах оборудования. Известно время обработки и последовательность обработки каждого изделия на каждом виде оборудова­ния {табл. 2.23).Требуется определить такую последовательность запуска изделий в производство (ремонт, обслуживание), чтобы суммарное время на изготовление (ремонт, обслуживание) всех изделий на двух видах обо­рудования было минимальным.

Таблица 2.23

Оборудование	И1	И2*	И3	И4	И5	И6
Oi	Время Тijизготовлениеj-го изделия наi-ом оборудовании изготовления j-roизделия наi-ом оборудовании
Оборудование 1	6	4	6	5	7	4
Оборудование 2	5	2	3	6	6	7

Выявление основных особенностей, взаимосвязей и количествен­ных закономерностей. Обозначим через Т_ij- время обработкиj-го изделия наi-ом оборудовании. Предполагается, что время перехода изделия от од­ного оборудования к другому незначительно и им можно пренебречь или включить в длительность операции. Каждое изделие обрабатывается снача­ла на первом оборудовании, затем на втором. Каждое обслуживание долж­но быть завершено прежде, чем начнется следующее.

Исходный порядок запуска изделий в производство (ремонт, обслужи­вание) выглядит так

И₁—> И₂—> И₃--> И₄--> И₅—»И₆.

Но этот порядок запуска изделий в производство может быть и не оп­тимальным.

Вначале обрабатывают первое изделие на первом оборудовании – O₁в течение 6 ед. времени – Т₁₁= 6. После освобождения первого оборудова­ния – О₁на нем начинают обрабатывать второе изделие в течение 4 ед. времени

Т₁₂= 4. Одновременно первое изделие начинают обрабатывать на втором оборудовании -O₂в течение 5 ед. времени

T₂₁= 5.

После обработки второго изделия на первом оборудовании - 0₅втор оборудование - О2еще занято обработкой первого изделия. И второе изделие ожидает в течение 1 ед. времени начала обработки на втором оборудовании - О₂.После обработки второго изделия на первом оборудовании - ( начинается обработка третьего изделия. После ожидания второго изделия течение 1 ед. времени начинается его обработка на втором оборудовании О₂в течение 2 ед. времени — Т22= 2. Однако, после завершения обработка третьего изделия на первом оборудовании второе оборудование будет простаивать

(4 + 6) - (5 + 2) = 3 ед. времени.

И так далее.

Из графика хорошо видно, что общая продолжительность изготовления (ремонта, обслуживания) всех изделий составит 41 ед. времени, однако имеются большие простои второго оборудования.

Построение математической модели. Критерий оптимизации представляет собой суммарное время обработки изделий на двух видах оборудования. Суммарное время обработки изделий Топределяется суммой простоев второго оборудования в ожидании изделий с первого оборудования времени обработки на втором оборудовании этих изделий.

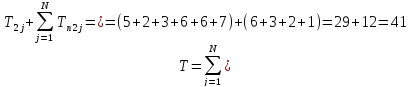
Где Т_2j- время обработкиj- х изделий на втором оборудовании;

Т_П2j- время простоя второго оборудования при изготовленииj- х изделий.

Так как время обработки изделий на втором оборудовании по услови задачи не изменяется, то уменьшение суммарного времени обработки изделий можно осуществить за счет изменения порядка запуска изделий в производство (ремонт, обслуживание).

Для решения этой задачи разработаны различные алгоритмы решения Рассмотрим один из наиболее простых, но часто используемых - алгоритм Джонсона.

Оптимизация запуска изделий в производство - это типичная комбинаторная задача. Решение этой задачи, также как и предыдущей представляя собой некоторую перестановку в порядке запуска изделий в производстве времени. Ее можно решить путем прямого перебора всех возможных вариантов запуска изделийв производство. Число вариантовN равноn! Таким образом, для нашей задачиN= 6! = 720 вариантов.

Алгоритм Джонсона резко сокращает и упрощает процесс поиска оптимального варианта запуск изделий в производство.

Алгоритм решения. Алгоритм Джонсона включает два этапа:

1. Нахождение наименьшего времени обработки изделия на двух вид оборудования. В табл. 2.23 ищется минимальное время и соответствующее изделие отмечается звездочкой. В нашей задаче это минимальное время обработки 2-го изделия на втором оборудовании;

2. Изменение порядка запуска изделий в производство. Здесь возмож­ны различные варианты:

• если наименьший элемент (время обработки изделия) относится к пер­вому виду оборудования, то изделие первым запускается в производст­во (ремонт, обслуживание), его перемещают в начало второй таблицы (табл. 2.24), аналогичной табл. 2.23;

• если наименьший элемент (время обработки изделия) относится к вто­рому оборудованию, то изделие последним запускается в производство (ремонт, обслуживание), его перемещают в конец второй таблицы {табл. 2.24), аналогичной табл. 2.23;

• если имеется несколько наименьших элементов (время обработки изделия) и они относятся к первому (второму) оборудованию, то изде­лие первым (последним) запускается в производство (ремонт, обслужи­вание), которому соответствует наименьший элемент для другого обо­рудования, т.е. его перемещают в начало (конец) второй таблицы (табл. 2.24), аналогичной табл. 2.23;

• если наименьшие элементы (время обработки изделия) относятся как к первому, так и к второму оборудованию, то изделия перемещают в на­чало или конец второй таблицы (табл. 2.24), аналогичной табл. 2.23 согласно вышеизложенным правилам.

Перемещаемое изделие помечается звездочкой и в дальнейшем перено­су не подлежит и при дальнейшем расчете не учитывается.

В нашей задаче минимальный элемент относится ко второму виду обо­рудования, следовательно, изделие с минимальным временем обработки на втором оборудовании должен обрабатываться последним. Это изделие, а точнее весь столбец, отмеченный звездочкой, полностью переносится в конец второй таблицы - табл. 2.24.

Таблица 2.24

Оборудование Oi	И1			И3		И4	И5		И6		И2*
	Время Тijизготовлениеj-го изделия наi-ом оборудовании изготовления j-roизделия наi-ом оборудовании
Оборудование 1	6			6		5	7		4		4
Оборудование 2	5			3		6	6		7		2
Номер итерации		-	-		-		-	-		1

После перемещения изделия в начало, конец таблицы алгоритм расче­та повторяется с этапа 1 до тех пор, пока можно изделия перемещать. Пе­ремещенные изделия (изделия отмеченные звездочкой) в дальнейших пе­ремещениях не участвуют.

В нижней строке указан номер итерации, на которой было произведе­но перемещение в данную позицию данного изделия.

Окончательная таблица запуска изделий в производство (ремонт, служивание) для нашей задачи будет выглядеть так как в табл. 2.25.

Таблица 2.25

Оборудование Oi	И6			И4*		И5	И1*		И3*		И6
	Время Тijизготовлениеj-го изделия наi-ом оборудовании изготовления j-roизделия наi-ом оборудовании
Оборудование 1	4			5		7	6		6		4
Оборудование 2	7			6		6	5		3		2
Номер итерации		3	4		5		4	2		1

Таким образом, оптимальный порядок запуска изделий в производстве будет выглядеть так

И₆—>И₄—>И₅—> И₁—> И₃--> И₂

Суммарное время обработки изделий Топределяется суммой простоев второго вида оборудования в ожидании изделий с первого вида оборудова-] ния и времени обработки на втором виде оборудования этих изделий.

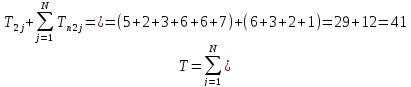
В некоторых частных случаях алгоритма Джонсона применим и для решения задач запуска изделий в производство (ремонт, обслуживание), требующих трехэтапного обслуживания (обработка на трех видах оборудования).Это возможно в тех случаях, когда выполняется одна из следующих систем неравенств:

1/ минимальное время обработки изделий на первом виде оборудова­ния больше или равно максимальному времени обработки изделий на вто­ром виде оборудования

min { T_ij } > max { T_2j }, (j = 1, ,n);

2/ минимальное время обработки изделий на третьем виде оборудова­ния больше или равно максимальному времени обработки изделий на вто­ром виде оборудования

min{T_3j} >max{T_2j },(j=1,…,n).

После этого составляется новая таблица, в которую вместо Ту заносит­ся сумма (T_ij ,T_2j) или вместо T_2j - сумма (T_2j + T_3j), а затем применяется ал­горитм Джонсона.

Оптимизация запуска изделий в производство (ремонт, обслуживание) позволяет существенно сократить время простоев оборудования и рабочих, длительность производственного цикла изготовления изделий.

\епло наших телзмер транспортной партии

линии. игателя конвейеральность линии равна величине, обратной такту линии.

рованных пер