9.2. Смешанное расширение биматричной игры

Если определить смешанные стратегии игроков 1и2 для биматричной игры с помощью (4.1.1, 4.1.2) с учетом (4.1.3, 4.1.4), то мы получим смешанное расширениебиматричной игры.

Средние выигрыши игроков 1и2 (математические ожидания результатов) при использовании смешанных стратегий

(9.2.1)

где ,векторы вероятностей использования чистых стратегий.

Для биматричной игры cмешанные стратегиииобразуютситуацию равновесияпо Нэшу в смешанных стратегиях, если

(9.2.2)(9.2.3)

Равновесные выигрыши игроков

(9.2.4)

Можно доказать существование ситуации равновесияпо Нэшу в смешанных стратегиях в любой биматричной игре.

Для того, чтобы в биматричной игре ситуация в смешанных стратегияхибыла ситуацией равновесия, необходимо и достаточно, чтобы для всех чистых стратегий, соответственно, игроков1и2 выполнялись условия

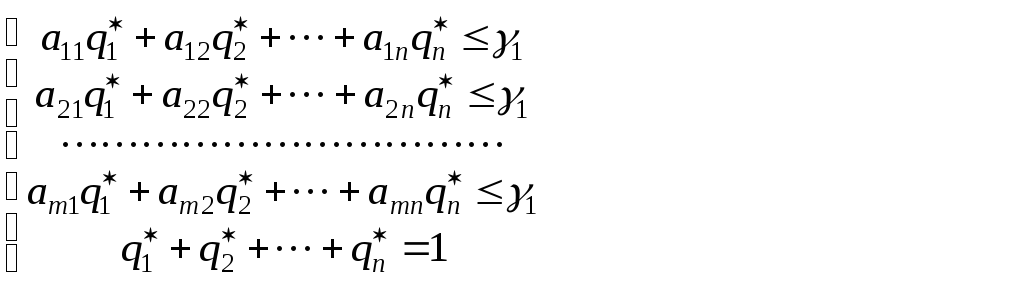(9.2.5)

(9.2.6)

В данном случае вспомогательные задачи линейного программирования

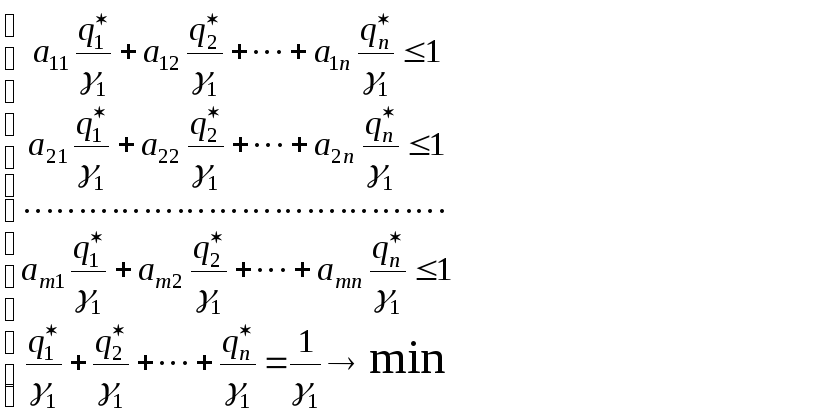(9.2.7)

(9.2.8)

С другой стороны, средний выигрыш игрока 1остается неизменным и равным равновесному выигрышуγ₁при равновесной смешанной стратегииигрока2 и любой чистой стратегии игрока 1

(9.2.9)

Средний выигрыш игрока 2остается неизменным и равным равновесному выигрышуγ₂при равновесной смешанной стратегииигрока1 и любой чистой стратегии игрока 2

(9.2.10)

Отсюда для примера 9.1 получим две системы линейных уравнений.

Система

имеет решение, состоящее из положительных величин

Система

тоже имеет решение, состоящее из положительных величин

Соответствующие (9.2.7), (9.2.8) (9.2.9), (9.2.10) вспомогательные задачи линейного программирования имеют вид

(9.2.11)

(9.2.12)

Отсюда для примера 9.1 получим

Решение

Решение

Соответствующие (9.2.7), (9.2.8) вспомогательные задачи линейного программирования не позволяют найти решение смешанного расширения биматричной игры.

Заметим, что смешанная равновесная ситуация по Нэшу с выигрышами γ₁=0.8 и γ₂=0.8 менее предпочтительна для игроков, чем каждая из ситуаций равновесия в чистых стратегиях. Если игра повторяется многократно, то игрокам имеет смысл сделать совместный выбор: с вероятностью 0.5 выбирать совместно ситуации (x₁,y₁) или (x₂,y₂). Тогда средний ожидаемый выигрыш игроков будет, очевидно, 2.5 и 2.5.

Лекция 10 неантагонистические игры n игроков

10.1. Бескоалиционная игра n игроков

Бескоалиционной неантагонистической игройnигроков (1, 2,…, n) называется игра, в которой игроки одновременно и независимо друг от друга выбирают свои стратегииⁱx,i=1, 2,…,n, в результате чего формируется ситуация (¹x,²x,…,ⁿx), после чего каждый игрок получает выигрышⁱa(¹x,²x,…,ⁿx),i=1, 2,…,n.

Ситуация (¹x^*,²x^*,…,ⁿx^*) называетсяситуацией равновесияпо Нэшу, если

(10.1.1)

Отклонение от ситуации равновесия по Нэшу двух и более игроков может привести к увеличению выигрыша одного из них.

Ситуация (¹x^*,²x^*,…,ⁿx^*) называетсясильно равновесной, если для любой коалиции игроковi₁,i₂,…,i_s

(10.1.2)

Это условие гарантирует нецелесообразность соглашения между игроками о вступлении в коалицию, так как в любой коалиции одного из игроков это соглашение не устраивает.

Ситуация (¹x^p,²x^p,…,ⁿx^p) называетсяситуацией оптимальнойпо Парето, если не существует ситуации (¹x, ²x,…, ⁿx), для которой имеют место неравенства

(10.1.3)

и хотя бы для одного j

(10.1.4)