4. Неоднородные системы

Пусть имеется система

,

или, в координатной форме,

(6)

Выпишем расширенную матрицу системы:

.

Приведем ее к ступенчатому виду. Возможны два случая:

а) В последнем столбце (-ом) имеется угловой элемент. В этом случае ранг расширенной матрицыоказался на 1 больше ранга матрицыА, и, значит, по теореме Кронекера–Капелли система несовместна. Этому случаю соответствует картинка:

Последней ненулевой строке расширенной матрицы соответствует уравнение типа (1'), не имеющее решений

3 (1')

б) В последнем (-ом) столбце угловой элемент отсутствует. В этом случае, т.е. ранги матрицыА и расширенной матрицы совпадают. По теореме Кронекера–Капелли решение есть. Картинка имеет вид:

Найдем решение системы. Переменные, соответствующие угловым элементам – главные или зависимые, остальные – свободные или независимые. Выпишем систему, соответствующую ступенчатому виду расширенной матрицы (она эквивалентна исходной системе) и все члены, содержащие свободные переменные, перенесем вправо. В левой части останутся зависимые переменные с коэффициентами, образующими верхнюю треугольную матрицу. Система примет вид:

Пусть для простоты х₁, ..., х_r – зависимые, а х_r+1, ..., х_n – свободные. Тогда система имеет вид:

На этом завершаем прямой ход метода Гаусса. Теперь сделаем обратный ход. Из последнего уравнения выражаем х_r через свободные переменные и подставляем полученное выражение в предпоследнее уравнение. Тогда предпоследнее уравнение позволяет выразить х_r-1 через свободные переменные. Полученные выражения для х_r, х_r-1 используем в 3-м с конца (предпредпоследнем) уравнении. Получаем выражение для х_r-2. И так далее. В результате приходим к системе вида

(7)

Эта система эквивалентна исходной. Она называется общим решением системы, записанным в координатной форме.

Особо отметим случай, когда , т.е.rank А максимален и равен числу переменных n. В этом случае свободных переменных нет и мы получаем единственное решение

или в векторной форме

.

Если же , т.е. свободные переменные присутствуют, система имеет бесконечное множество решений, определяемых значениями свободных переменных. Система (7) служит хорошей формой представления общего решения: свободные переменныех_r+1, ..., х_n принимают произвольные значения, а зависимые х₁, ..., х_r – соответствующие значениям свободных переменных и определяемые по формулам (7). Чтобы подчеркнуть этот факт, присвоим свободным переменным значения, равные произвольным константам с₁, ..., с_nr соответственно: , и перепишем систему (7) в виде:

(8)

Как и в случае однородной системы общее решение (8) можно представить в векторной форме. Для этого сначала находим общее решение в векторной форме соответствующей однородной системы

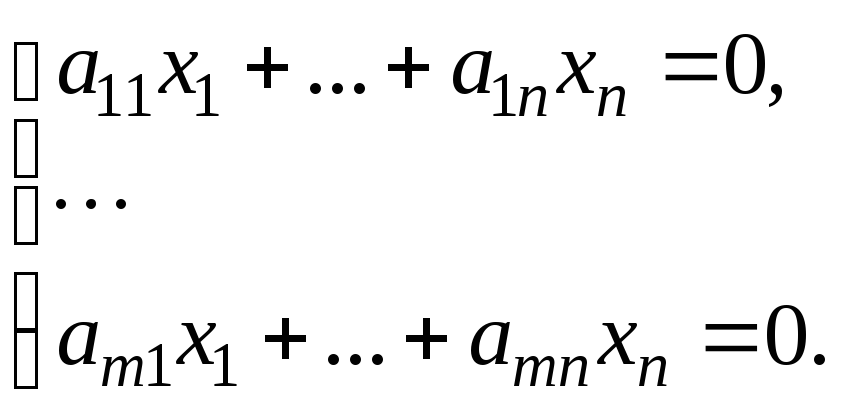(9)

Чтобы его получить, нет нужды повторять заново всю процедуру для однородной системы. Достаточно в (8) заменить нулями. Получим систему

, (10)

представляющую собой общее решение в координатной форме однородной системы (9). Придавая свободным переменным х_r+1, ..., х_n значения координат векторов

(составляющих стандартный базис в пространстве R^n-r свободных переменных), получаем с помощью (10) векторы

(11)

образующие ФСР, т.е. базис в подпространстве L решений однородной системы (9).

Линейная комбинация

векторов этого базиса есть общее решение в векторной форме однородной системы, то есть «произвольный вектор подпространства L (сокращение «оо» означает: общее решение однородной системы).

Остается найти частное решение неоднородной системы (6). Для этого проще всего положить в (7) значения свободных переменных равными нулю:

.

Получим с помощью (7) вектор:

(12)

(сокращение «чн» означает: частное решение неоднородной системы). Как мы знаем, общее решение неоднородной системы есть сумма частного решения неоднородной и общего решения однородной системы:

(«он» – общее решение неоднородной системы), или, подробнее,

, (13)

где с₁, ..., с_nr – произвольные постоянные. Формула (13) есть общее решение неоднородной системы в векторной форме. Здесь векторы ФСР определены формулами (11), аx^чн – формулой (12). Множество всех решений неоднородной системы есть сдвиг подпространства L всех решений однородной системы (общий элемент которого есть линейная комбинация ) на произвольный векторx^чн, представляющий собой частное решение неоднородной системы (результат сдвига не зависит от того, какое частное решение x^чн мы выберем). Если (13) расписать покоординатно, получим решение (8).