3. Метод Гаусса для получения общего решения однородной системы

Рассмотрим однородную систему (2). Мы можем переставлять уравнения местами, прибавлять к одному уравнению другое, умноженное на число, и всякий раз получать новую систему, эквивалентную старой, то есть имеющую то же самое множество решений. Эти операции удобней производить над строками матрицы А системы, и ясно, что они соответствуют элементарным преобразованиям строк. Приведем с помощью элементарных преобразований матрицу А к ступенчатому виду. Переменные х_i, соответствующие угловым элементам (т.е. имеющие те же номера, что и номера столбцов, содержащих угловые элементы) назовем главными или зависимыми, остальные – свободными или независимыми.

Выпишем систему, отвечающую ступенчатому виду

и перенесем в каждом уравнении все члены со свободными переменными вправо. Слева останутся выражения, содержащие только зависимые переменные. Система приобретет вид:

зависимые свободные

Пусть для простоты х₁, х₂, ..., х_r – зависимые, а х_r₊₁, ..., х_n – свободные. Тогда новая система имеет вид:

Итак, матрица коэффициентов при зависимых переменных – треугольная (квадратная матрица, все элементы которой, расположенные ниже главной диагонали, равны нулю) и при этом . Это былпрямой ход метода Гаусса.

Сделаем обратный ход: из последнего уравнения выразим х_r через свободные переменные и подставим полученное выражение в предпоследнее уравнение, затем выразим х_r_-1 через свободные переменные и подставим выражения для х_r, х_r_-1 в предыдущее («предпредпоследнее», т.е. (r  2)-е) уравнение и т.д. В результате получим выражения зависимых переменных х₁, х₂, ..., х_r через свободные х_r₊₁, ..., х_n

(3)

Выражения (3) задают множество решений однородной системы (2). Свободным переменным х_r₊₁, ..., х_n мы можем придавать любые значения (они играют роль произвольных параметров для множества решений системы) в то время как зависимые переменные получают соответствующие значения, вычисляемые по формулам (3). Всякий раз мы получаем некоторое решение, и все решения могут быть таким образом получены. Поэтому систему (3) называют общим решением в координатной форме системы (2). Иногда его представляют так:

(4)

где отчетлива видно, что свободным переменным х_r₊₁, ..., х_n отводится роль параметров с₁, ..., с_n__r .

Поскольку общее число зависимых и независимых переменных равно n, а число зависимых переменных равно рангу матрицы А, то размерность подпространства решений однородной системы

dim L =n- rank А.

Общее решение (3) позволяет найти базис в подпространстве L решений системы (2) и представить общее решение как произвольную линейную комбинацию элементов этого базиса. Свободным переменным х_r₊₁, ..., х_n будем последовательно придавать значения, соответствующие координатам векторов стандартного базиса в Rⁿ^^r:

Наборам е₁, ..., е_n__r свободных переменных соответствуют векторы

составляющие базис в L.

Определение. Базис в подпространстве решений однородной системы называется фундаментальной системой решений (ФСР).

Линейная комбинация элементов ФСР

(5)

есть произвольный вектор из L. Запись (5) называется общим решением в векторной форме системы (2).

Итак, размерность подпространства L есть n  r, где . Чем меньшеrank А, тем большую размерность имеет L и наоборот. В случае, когда (т.е.А имеет «полный ранг»), , т.е.L имеет нулевую размерность, и, значит, состоит лишь из нулевого вектора . В этом случае (2) имеет единственное нулевое решение.

Пример. Решить систему

Матрица системы

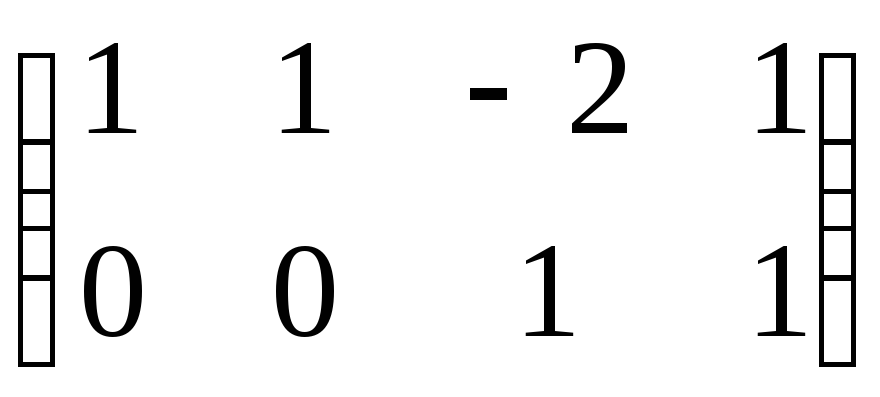
уже имеет ступенчатый вид. Значит, прямой ход метода Гаусса делать не нужно. Зависимые переменные – это х₁ и х₃ (соответствуют угловым элементам матрицы), свободные – х₂ и х₄.

Перенесем члены со свободными переменными вправо: