Лекция 10. Системы линейных алгебраических уравнений

1. О совместности системы

Рассмотрим систему m уравнений с n неизвестными:

(1)

Положим

.

Здесь A – матрица системы, х – неизвестный вектор, b – вектор правых частей.

Матрично-векторная запись системы:

_.

Система, имеющая хотя бы одно решение х, называется совместной, в противном случае – несовместной.

Обозначим

– столбцы матрицы А. Тогда систему можно записать в виде:

.

Из этой записи видно, что решить систему – значит представить вектор b как линейную комбинацию столбцов А₁, ..., А_n матрицы А, причем х₁, ..., х_n – коэффициенты этой линейной комбинации. Это представление возможно, если добавление вектора b к столбцам А₁, ..., А_n не повышает ранга системы столбцов. Значит, совместность системы (1) эквивалентна тому, что расширенная система векторов {А₁, ..., А_n, b} имеет тот же ранг, что и система {А₁, ..., А_n}.

Сформулируем то же самое на языке матриц. Введем матрицу

,

т.е. добавим к А столбец b.

Назовем расширенной матрицей. Из сказанного выше вытекает:

Теорема 1 (Кронекера–Капелли). Система (1) совместна тогда и только тогда, когда (т.е. ранги матрицы системы и расширенной матрицы совпадают).

Пример. Решить систему

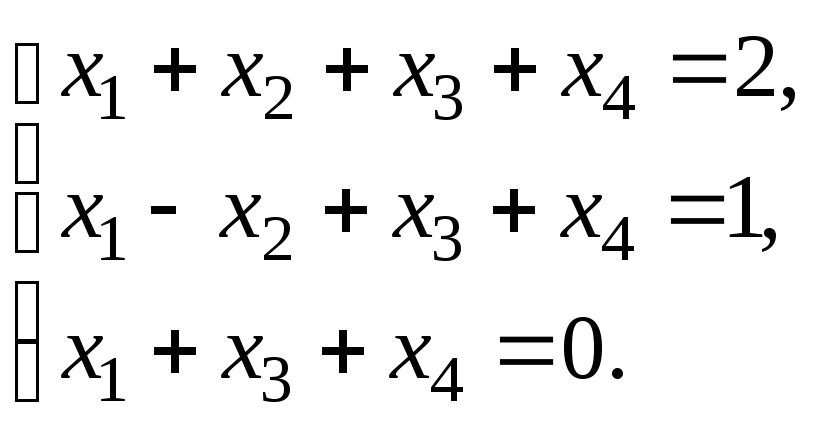
Запишем расширенную матрицу и вычислим ее ранг (и одновременно ранг матрицы системы А).

система несовместна.

Действительно, последнее уравнение в новой системе, соответствующее последней строке матрицы, имеет вид:

3 (1')

– решений нет.

2. Однородная и неоднородная системы

Если , система (1) называется неоднородной. Соответствующая однородная система имеет вид:

(2)

или, коротко

.

Однородная система всегда совместна, поскольку всегда имеет нулевое решение

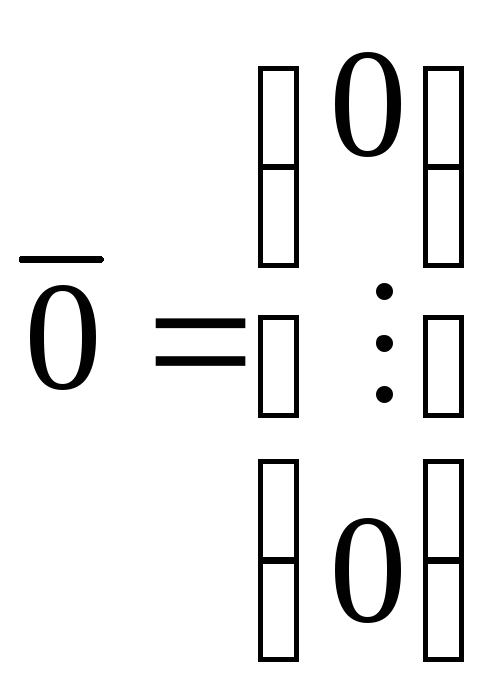
Вопрос лишь в том, единственно ли это решение, и если нет, что собой представляет множество всех решений?

Теорема 2. Множество всех решений однородной системы является подпространством в Rⁿ.

Доказательство. Если х⁰ – решение, т.е. , и– число, то– тоже решение, ибо. Кроме того, еслих¹ и х² – решения, т.е. , то и– решение, ибо.

Между решениями однородной и неоднородной систем имеется простая связь.

Теорема 3. Решение однородной системы плюс решение неоднородной системы есть решение неоднородной системы.

Доказательство. Пусть х⁰ и х¹ таковы, что . Тогда.

Теорема 4. Разность двух решений неоднородной системы есть решение однородной.

Доказательство.

. 

С помощью теорем 2–4 можно понять, как устроено множество решений неоднородной системы . Надо взять подпространство

решений однородной системы и «сдвинуть» его на произвольный вектор х¹ – решение неоднородной системы, т.е. такой, что . Получим множество

,

состоящее из всех векторов вида , где– произвольное решение однородной системы. (Множествоне зависит от того, какое «частное» решениех¹ однородной системы мы возьмем.) Этот факт формулируют следующим образом: общее решение неоднородной системы есть частное решение неоднородной системы плюс общее решение однородной. Имеется ввиду, что если частное решение неоднородной х¹ фиксировано, а х⁰ «пробегает» все множество решений однородной системы, то сумма «пробегает» все множество решений неоднородной системы.

Сначала мы научимся находить общее решение однородной системы, а затем – общее решение неоднородной.