Лекция 11

ЛЕКЦИЯ 11. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

Задача 1. Решить систему

.

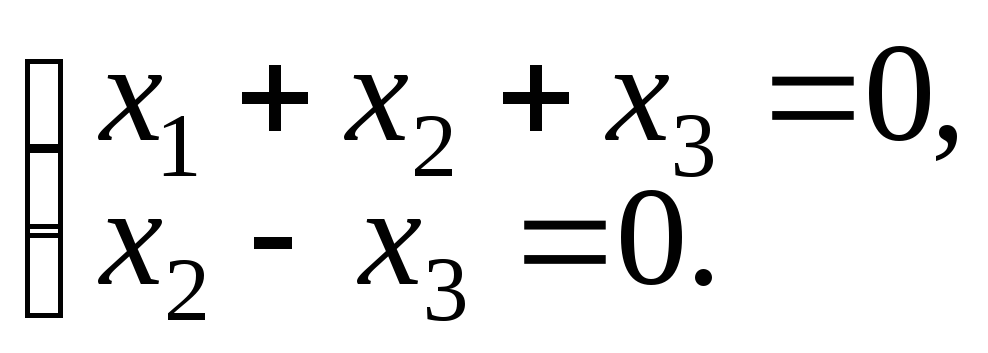Решение. Системе двух уравнений с тремя неизвестными соответствует матрица системы

.

Матрица А имеет ступенчатый вид, угловые элементы выделены жирным шрифтом  прямой ход метода Гаусса выполнять не надо. Каждый столбец матрицы состоит из коэффициентов при переменных, которые написаны сверху над столбцами. Переменные , в столбцах которых есть угловые элементы, являются главными или зависимыми; - свободная или независимая переменная. Положим и выразим главные переменные через параметр :

Мы нашли общее решение в координатной форме.

Размерность подпространстве решений однородной системы равна количеству независимых переменных, т.е. одному. Базис (ФСР) в подпространстве решений однородной системы состоит из одного вектора, который можно получить, выбрав и записывая решение в виде вектора:

Общее решение однородной системы в векторной форме – разложение общего решения по ФСР имеет вид

.

Задача 2. Найти общее решение и фундаментальную систему решений однородной системы . Разложить общее решение по Ф.С.Р. Матрица задана.

Решение. Выпишем систему уравнений в координатной форме

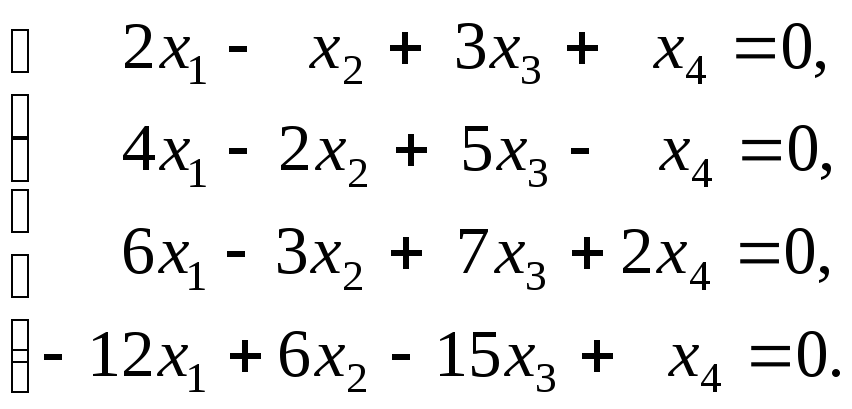
Поскольку вектор правых частей равен нулевому вектору, т. е. , то система уравнений является однородной.

Методом Гаусса приведем систему уравнений к ступенчатому виду. Выпишем матрицу и преобразуем ее:

.

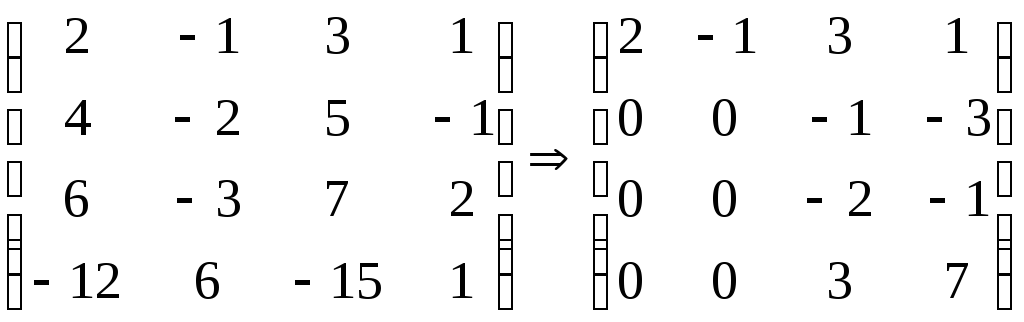На первом шаге первую строку не меняем (в верхнем левом углу стоит ведущий элемент ); из второй строки вычитаем первую, умноженную на 2, и результат запишем во вторую строку; из третьей строки вычитаем первую, умноженную на 3, и результат запишем в третью строку; к четвертой строке прибавляем первую, умноженную на 6, результат запишем в четвертую строку. Условно эти элементарные операции можно записать так: .

Далее применим элементарные операции: . Получаем:

.

После чего к четвертой строке, умноженную на 5, прибавим третью строку, умноженную на 2, результат запишем в четвертую строку, т. е. :

Матрица приведена к ступенчатому виду. Мы выполнили прямой ход метода Гаусса.

Число угловых элементов (отмечены) равно трем, следовательно, ранг матрицы .

Находим общее решение однородной системы в координатной форме:

а) Главными (зависимыми) назовем переменные х₁, х₃ и х₄, так как угловые элементы являются коэффициентами перед х₁, х₃ и х₄ в ступенчатой системе, переменная х₂ – свободная (независимая). Свободную переменную обозначим как .

б) Выпишем ступенчатую систему уравнений, эквивалентную исходной:

в) Выразим зависимые переменные через свободную из ступенчатой системы (обратный ход метода Гаусса), начиная с последнего уравнения и подымаясь “вверх” по системе уравнений. Из третьего уравнения получим: . Из второго уравнения имеем: . Из первого уравнения получим: .

Формулы

выражающие главные переменные х₁, х₃ и х₄ через свободную переменную (параметры), определяют параметрическую запись решения системы. Эти формулы задают общее решение системы в координатной форме.

Теперь получим решение однородной системы в векторной форме. Поскольку ранг матрицы , а размерность системы n=4, система имеет бесконечное множество решений. Решения однородной системы образуют подпространство V пространства R⁴ размерности

.

Базис подпространства решений однородной системы состоит из одного вектора . Базис подпространства V решений однородной системы называется фундаментальной системой решений.

Пусть свободная переменная принимает значение , получим вектор-решение . Этот вектор может служить фундаментальной системой решений однородной системы уравнений. Тогда любой вектор-решение запишется в виде:

где – произвольная константа. Формула определяет общее решение однородной системы в векторном виде.

Задача 3. Решить систему (найти общее решение в координатной и векторной форме)

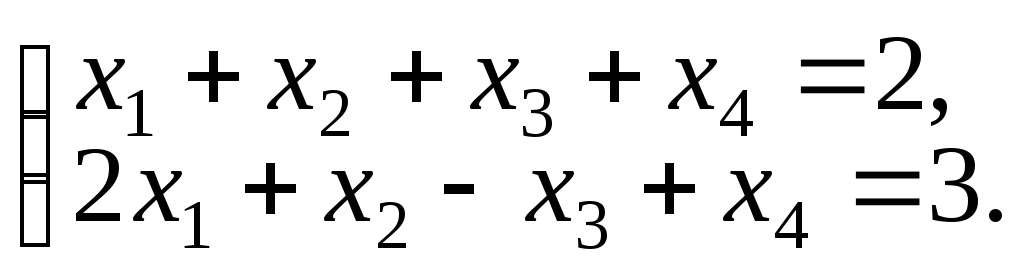
Решение. Расширенная матрица имеет вид:

.

Вычитая из 2-й строки 1-ю, умноженную на 2, получаем ступенчатый вид этой матрицы

,

.

Следовательно, система совместна: х₁, х₂ – зависимые переменные, х₃, х₄ – свободные.

Новая система имеет вид:

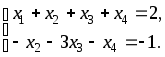
Переносим члены со свободными переменными вправо:

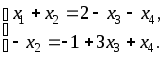
Закончился прямой ход метода Гаусса. Теперь – обратный ход. Из последнего уравнения получаем

.

Подставляем в первое:

откуда

.

Итак,

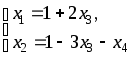
– общее решение в координатной форме неоднородной системы.

Найдем векторную форму. Для этого заменим в общем решении свободные члены нулями:

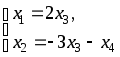
Получаем общее решение однородной системы

1) Пусть ,

.

2) Пусть ,

.

Следовательно,

.

Найдем частное решение неоднородной системы. Полагая в общем решении неоднородной системы , получаем: . Следовательно,

.

Итак,

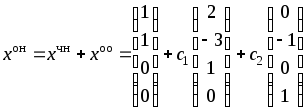
– общее решение в векторной форме.

Задача 4. Решить систему

Решение. Выпишем расширенную матрицу системы и приведем ее к ступенчатому виду:

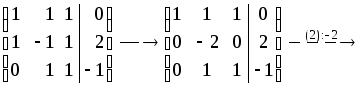
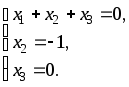
Получили систему ступенчатого вида эквивалентную исходной системе. Все три переменные главные, свободных переменных нет. Решение единственно:

.

Задача 5. Исследовать совместность системы, и в случае совместности найти общее или единственное решение системы уравнений в координатной и векторной формах. Матрица А и вектор заданы.

.

Решение. Методом Гаусса приведем систему уравнений к ступенчатому виду. Выпишем расширенную матрицу и преобразуем ее:

.

На первом шаге первую строку не меняем (в верхнем левом углу стоит ведущий элемент ); вторую строку не меняем (в первом столбце стоит нуль); из третьей строки вычитаем первую, умноженную на 2, и результат запишем в третью строку; из четвертой строки вычитаем первую, умноженную на 3, результат запишем в четвертую строку. Обратите внимание, что последний столбец меняется аналогично другим столбцам. Условно эти операции можно записать так: .

Далее применим элементарные операции: . Получаем:

.

Угловые элементы (отмечены) определяют, что ранги матрицы системы и расширенной матрицы совпадают:

 по теореме Кронекера-Капелли система уравнений совместна, а так как , то система имеет бесконечное множество решений.

Закончился прямой ход метода Гаусса. Найдем общее решение системы в координатной форме:

а) Главными (зависимыми) назовем переменные х₁ и х₂, так как угловые элементы являются коэффициентами перед х₁ и х₂ в ступенчатой системе, остальные переменные х₃, х₄ – свободные (независимые). Свободные переменные обозначим как , .

б) Выпишем ступенчатую систему уравнений, эквивалентную исходной:

в) Выразим зависимые переменные через свободные из ступенчатой системы (обратный ход метода Гаусса), начиная с последнего уравнения и подымаясь “вверх” по системе уравнений. Из второго уравнения получим: , из первого уравнения имеем: .

Формулы

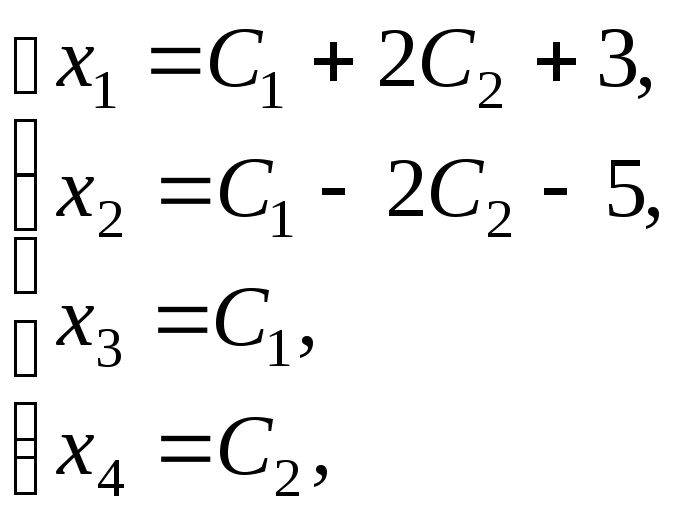
выражающие главные переменные х₁, х₂ через свободные переменные (параметры), определяют параметрическую запись решения системы. Давая свободным переменным любые значения и вычисляя х₁ и х₂, получим решение системы , причем любое решение системы можно получить по этим формулам. Мы нашли общее решение системы в координатной форме.

Теперь найдем общее решение неоднородной системы в векторной форме. Для этого нужно найти общее решение соответствующей однородной системы и прибавить к нему некоторое частное решение неоднородной системы.

а) Выпишем соответствующую однородную систему уравнений , приведенную к ступенчатому виду. Она только свободными членами отличается от ступенчатой неоднородной системы

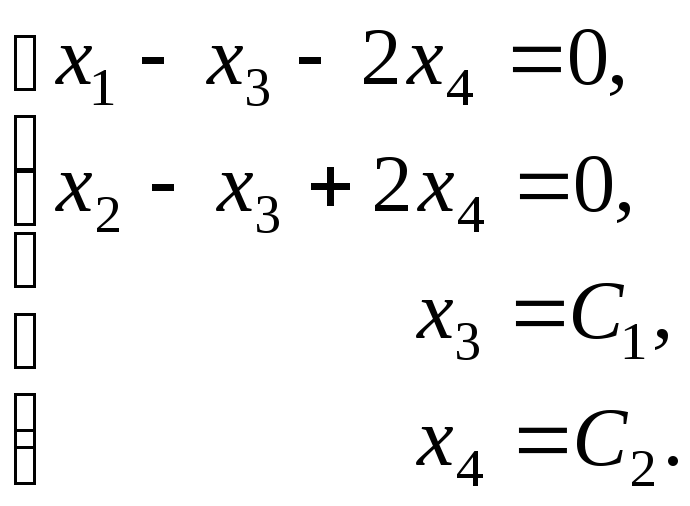
Ранг системы r равен 2, размерность системы n равна 4, система имеет бесконечное множество решений. Решения однородной системы образуют подпространство V пространства R⁴ размерности

.

Базис подпространства решений однородной системы состоит из двух векторов . Это могут быть любые два линейно независимые решения системы . Напомним, что базис подпространства V решений однородной системы называется фундаментальной системой решений.

б) Выразим зависимые переменные х₁, х₂ через независимые х₃, х₄

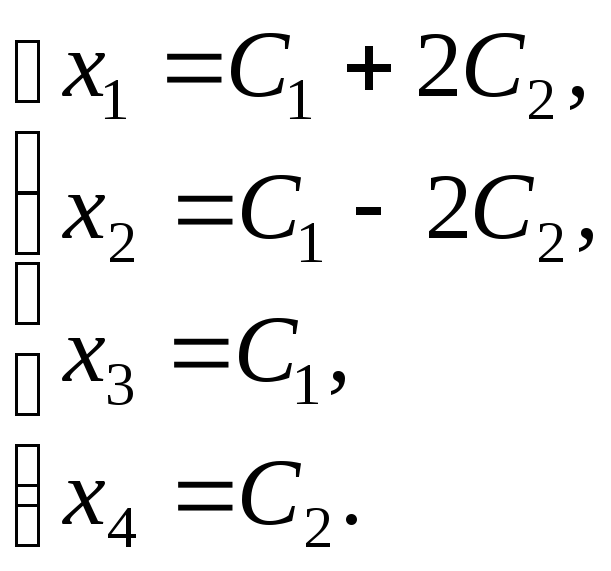
в) Пусть, например, свободные переменные принимают значения , тогда , получим вектор-решение ; если , то получим вектор-решение . Пара линейно независимых векторов может служить фундаментальной системой решений однородной системы уравнений. Тогда любой вектор-решение запишется как линейная комбинация базисных решений:

,

где – произвольные константы.

Последняя формула определяет общее решение однородной системы в векторном виде.

г) Найдем какой-нибудь вектор-решение неоднородной системы . Используем для этого параметрическую (координатную) запись решения неоднородной системы

Положим, например, , тогда . Вектор является некоторым частным решением неоднородной системы.

д) Теперь запишем общее решение неоднородной системы в виде

.

Эта последняя запись является векторной записью общего решения неоднородной системы в виде суммы частного решения неоднородной системы и общего решения однородной системы .