Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Харьковский Национальный Университет им. В. Н. Каразина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

методичка черногор

.pdf

Скачиваний:

Добавлен:

23.02.2015

Размер:

1.52 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1211 12 > Следующая >>>

Приложение

9. ln (1− x)= −x −

−

...−

−...,

−1 ≤ x <1;

10.shx = x +

x2n+1

+..., x R;

+...+

(2n +1)!

11.chx =1+

x2n

x R.

+...+

+...,

(2n)!

5.Некоторые интегралы, наиболее часто встречающиеся при решении задач.

1.∫dxx = ln x +C;

2.∫eax dx = 1a eax +C;

3.∫ x2 dx+ a2 = 1a arctg ax +C, a ≠ 0;

4. ∫

x −a

+C,

a ≠ 0;

x2 −a2

x + a

5. ∫

a − x

+C,

a ≠ 0;

a2 − x2

a + x

6.∫tgxdx = −ln cos x +C;

7.∫ctgxdx = ln sin x +C;

8. ∫ax dx =

+C, a > 0, a ≠1;

ln a

∫

= arcsin

+C,

< a, a ≠ 0;

− x

10.

∫

= ln

x +

a2 + x2

+C, a ≠ 0;

+ x

10. ∫

= ln

x +

x2 −a2

+C,

, a ≠ 0;

− x

11.∫sin2 mxdx = 12 x − 41m sin 2mx +C;

12.∫cos2 mxdx = 12 x + 41m sin 2mx +C;

13.

+∞∫ e−x2 dx =

π;

−∞

+∞

−a2x2

n +1

14. ∫ e

dx =

a > 0, n > −1;

n+1

−∞

15.

+∞∫ e−ax2 ± px dx =

πe−

a > 0;

−∞

16.

+∞∫ e−ax2 cos mxdx =

e−m4a2

, a > 0;

−∞

Приложение

17.	∞∫e−ax cos mxdx =			a		,	a > 0;
		a	2	+ m	2
	0

18. +∞∫ f (x)δ(x − x0 )dx = f (x0 ), где f(x) непрерывна в x0.

−∞

6.Некоторые физические константы.

1.Скорость света в вакууме c ≈ 3 108 м/с;

2.Элементарный заряд e ≈ 1,6 10−19 Кл;

3.Масса покоя электрона m ≈ 9,1 10−31 кг;

4.Постоянная Больцмана k = 1,38 10−23 Дж/К.

100

Ответы

ОТВЕТЫ

2.1

(x,t )= E cos k

а)

; E

x −

;

1 2

™

+αE)

ε0

(1+αE )

H (x,t )

1 2

= ±ε0

б)

;

E (x,t )= E

cos k

x −

; H

(x,t )

= ±

E +

α E3

1+αE

vф =

;

E (x,t )= E0 cos k0 x −

;

3αE2

+3αE2

в)

+3αE

ln ( 3αE + 1+3αE

)

α ≥ 0; ±

;

H (x,t )=

(arcsin

E2 ).

α < 0; ±

E +

E 1−3

г)

ε0

(±(1

+ αE )

−1).

vф =

; E

−

ε0 (1+αE )

(x,t )= E0 cos k0 x

; H (x,t )= ±

ε0 (1+αE )

3α

2.2

а)

AeaA = A eaA0 e−k0 ,

при k

>>1

A ≈ A eaA0 e−k0 ; P ≈ eaA0 ;

a1) a>0, P>1; a = A

−1

, P ≈ 2,78;

a2) a<0, P<1; a = −A−1 , P ≈ 0,38;

a3) a=0, P=1.

а4) a = A0−1, A(x)≈ A0e−

α0x ;

а5) a = −A0−1, A(x)≈ A0 (1− 1−e−α0x );

б)

A =

A e−k0

−k

при k0 >>1

A ≈

Ae−k0

;

P ≈

;

1+ aA

(1−e 0 )

1+ aA

+ aA

б1) a>0, P<1; a = A

−1

, P = 0,5;

б2) a<0, P>1; a = −A0−1 , P = ek0 >> 1;

б3) a=0, P=1.

101

Ответы

б4) a = A0−1, A(x)≈

A e−α0x

;

1+α0 x

б5) a = −A0−1,

A(x)≈

A e−α0x

;

1−α0 x

a A3

a A03

−k

при k

>>1

A ≈ A e

−k

a A03

в) Ae3

= A e3

0 e3

;

P ≈ e3 ;

в1) a>0, P>1; a = A−3 ,

P ≈1,4;

в2) a<0, P<1; a = −A−3 ,

P ≈ 0,7;

в3) a=0, P=1.

в4) a = A0−3 , A(x)≈ A0e−2α0x ;

в5) a = −A0−3 , A(x)≈ A0 (1− 1−e−α0x );

;

при k

>>1

b 2

г) AeaA+2 A

= A eaA0 +2 A0

A ≈ A eaA0 +2 A0 e−k0 : P ≈ eaA0 +

2 A0

;

г1) a>0, b ≥ 0, P>1; a = A−1

, b = A−2

P ≈ 4,6;

г2) a>0, b<0

г21)

a >

A , P >1;

= A−1

b = A−2

P ≈1,7;

г22) a =

A ,

P =1;

г23)

a <

A ,

P <1;

г3) a=0, b>0, P>1.

г4) a=0, b=0, P=1.

г5) a=0, b<0, P<1.

г6) a<0, b>0

г61)

1 bA ,

P >1;

г62)

1 bA ,

P =1;

г63)

1 bA ,

p <1;

= −A−1,

b = A−2

, P ≈ 0,6 ;

a = −A−1,

b = A−2 ,

г7) a<0, b<0, P<1;

P ≈ 0,2 .

г8) a = A0−1,

A(x)≈ A0e−2α0x ;

г9) a = −A0−1, A(x)≈ A0 (1− 1−e−α0x );

2.3

α20

a) P

= eaA10 α10 ;

a1) a>0, P12>1; a2) a<0, P12<1;

a3) a=0, P12=1.

α20

б) P12 = (1+ aA10 )α10 ; б1) a>0, P12<1; б2) a<0, P12>1; б3) a=0, P12=1.

102

Ответы

α20

в) P

= e

;

в1) a>0, P12>1;

в2) a<0, P12<1;

в3) a=0, P12=1.

α20

aA10

A10

г) P

= e

α10 ; г1) a>0, b ≥0, P12>1;

г2) a>0, b<0; г21) a > 1

A ,

>1;

г22) a = 1

A ,

г23) a <

A ,

<1;

=1;

г3) a=0, b>0, P12>1, г4) a=0, b=0, P12=1, г5) a=0, b<0, P12<1.

г6) a<0, b>0:

г61)

< 1 bA ,

>1 ; г62)

= 1 bA ,

=1 ;

г63)

> 1 bA ,

<1; ;

г7) a<0, b<0, P12<1.

2.4

a1ω

a) Δϕ

нл

(x) ≈

A (1−e−α0xea2 A0 ) +

−e−2α0xe2a2 A0 );

α0c

Δϕ

→

a1ω

;

нл

x→∞

a A e−α0x

α0c

ω a

ω a1

1+ a A e−α0x

б) Δϕнл(x) ≈ α c a

1+ a A

; Δϕнл

x→∞ → α c a ln (1+ a2 A0 );

в) Δϕнл(x) ≈

−2

x+2a A

−3α

x+3a A

(1−e

2 0 ) +

(1−e

2 0 )

α0c

Δϕнл

→

a1ω

A03

;

x→∞

α0c

г) Δϕнл(x) ≈

−2α

a A2

−4

2a A2

(1−e

2 0 )

(1−e

2 0

)

;

α0c

Δϕ

→

a1ω

A02

;

нл

x→∞

α0c

2.5

ω bL10

1+ aA0

a) Δϕнл =

; A

A e−k0

;

1+ aA

1+ aA (1−e−k0 )

→ ω

bL10

Δϕ

нл

ln (1+ aA );

x→∞

б) Δϕнл

bL10

− A +

(A0

− A

)

;

AeaA = A0eaA0 e−k0 ;

103

Ответы

Δϕ

→

ωbL

A +

;

нл

x→∞

в) Δϕнл =

ω bL10

1+ aA0

A e−k0

−k

;

A0 − A −

; A

1+ aA

(1−e 0 )

ω bL

Δϕнл

→

−

(1+ aA0 )

;

x→∞

г) Δϕнл =

ωbL10

(A02 − A2 )+

(A03

− A3 ) ;

AeaA = A0eaA0 e−k0 ;

Δϕнл

x→∞ →

ωbL10

aA0

3.1

1−eξ/ ξ0

a) и в) v(ξ) =

; ξ0 = v

б) и г) v(ξ) = v0 1+eξ/ ξ0

; ξ0 =

1+eξ/ ξ0

3.2

2v0

a) и в) v(ξ) =

ξ0 =

б) и г) v(ξ) =

; ξ0 =

;

1+e

ξ/ ξ0

4αv0

2ξ/

ξ0

αv0

3.3

u v; ξ0 vv0 .

3.4

e−

αξ

; αξ >>1;

αξ

а) v(ξ) ≈ v e− u

б) v(ξ) ≈ v e−|u| e−

|u| ; αξ >>1;

αξ

в) v(ξ) ≈ −v e− u

e− u ; αξ >>1;

г) v(ξ) ≈ −v e−|u| e−

|u| ; αξ >>1.

3.5

; L 1.

u v;

ξ ν v

3.6

1−eξ/ ξ0

a) и в) v(ξ) =

; ξ0 = v

б) и г) v(ξ) = v0 1+eξ/ ξ0

; ξ0 =

1+eξ/ ξ0

3.7

u 3αv2

;

3αv2

104

Ответы

4.1

a) v (ξ)=

;

ξ0 =

;

ch ξ ξ0

б) v (ξ)=

;

ξ0 =

;

ch ξ ξ0

4.2

;

ξ0

β.

6α

4.3

v0 u; ξ0

β.

4.5

′

1+u

1 +u

v (ξ)=

;

v (ξ)= ±

ξ2

4.6

u1 (u1 −2u2 )

v (x,t )=

ch−1 (

u1 (u1 −2u2 )(x −u1t )) exp

(x −u2t )

2β

4.7

v (ξ)= v (0)ch

−1

; v (0)=

;

ξ0 =

D .

4.9

v(0)

а) v(ξ) =

v(0) = 3u,

= 2

β/ u,

β =

ch2 (ξ/ ξ0 )

б) v(ξ) =

v(0)

v(0) = 3u,

= 2

β/ u,

β = βu2 ,

ch2 (ξ/ ξ0 )

в) v(ξ) =

v(0)

v(0) = 3u,

= 2

β/ u,

β =

u3 ,

2 (ξ/ ξ0 )

г) v(ξ) =

v(0)

v(0) = 3u =

= 2

β/ u = 2

βu, u = 1

β = βu2 ,

2 (ξ/ ξ0 )

4.10

β,

u =

;

а) v(ξ) = ch2 (ξ/ ξ0 )

; vm = 3u =

; ξ0 =

= u

α , β =

105

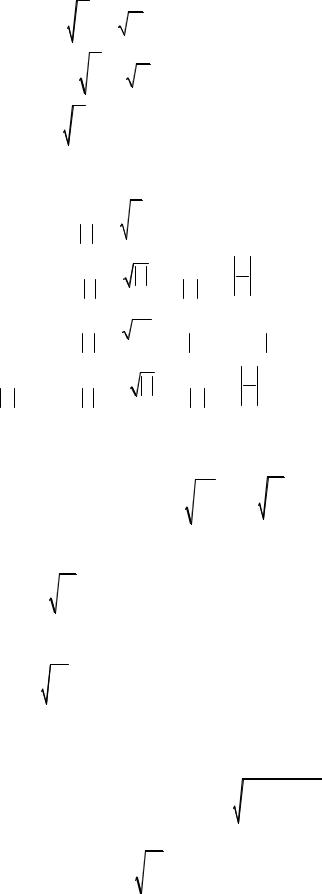
Ответы

б) v(ξ) =

vm = 3u =

u =

ch2 (ξ/ ξ0 )

;

ξ0 = 2

= u

β =

αu

;

в) v(ξ) =

vm = 3u =

, u =

ch2 (ξ/ ξ0 )

;

ξ0 = 2

u =

, β =

;

г) v(ξ) =

vm = 3u =

;

ξ0

= 2

u , u =

β =

;

ch2 (ξ/ ξ0 )

αu

αu2

4.11

а)		v	;	vm = 3u =	3u2
а)	v(ξ) = ch2 (ξ/ ξ0 )		;	vm = 3u =		α
		m

б)		v	;	vm = 3u =	3u2
б)	v(ξ) = ch2 (ξ/ ξ0 )		;	vm = 3u =		α
		m

в)		v	;	vm = 3u =	3u2
в)	v(ξ) = ch2 (ξ/ ξ0 )		;	vm = 3u =		α
		m

г)		v	;	vm = 3u =	3u2
г)	v(ξ) = ch2 (ξ/ ξ0 )		;	vm = 3u =		α
		m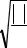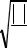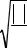

;ξ0 = 2

βu = 2

βu = 2 βu = 2

βu = 2u

β	,	u =	u2		, β =	βu		;
u				α			α

β, u = u2 , β = β u2 ;

αα

βu , u = u2 , β = β u3 ; αα

β, u = u2 , β = β u4 .

αα

4.12

а) не имеет,

б) имеет при ξ = x +ut, u > 0,

v(ξ) =

, vm =

α < 0,

, ξ0

ch(ξ/ ξ0 )

4.13

а) v(ξ) =

v(0)

v(0) = 3u,

= 2

u = u −α, α < u, ξ = x −ut

или ξ = x −ut , где

ch2 (ξ/ ξ0 )

α)t,

t = (1−

б) v(ξ) =

v(0)

v(0) = 3u, ξ

= 2

, u = u(1+α), α ≥ −1,

ξ = x −ut

или ξ = x −ut , где

ch2 (ξ/ ξ0 )

t = (1+α)t.

5.1

A1 (0)

A0 A1 (0)

a) A1 (t )=

;

A2 (t )=

A2∞th

∞ =

γ1

;

A0 A1

(

A2∞

2γ2 A1 (

γ2

0)A0

A2∞

A2 (0)

б) A1 (t )= A1∞thγ2 A1∞t;

A2 (t )

;

A1∞ =

A2 (0);

chγ

1∞

106

Ответы

в) A1 (t )

A1 (0)

;

A2 (t )= A2∞thγ1 A2∞t;

A2∞ =

(0);

chγ

2∞

г) A1 (t )= A1 (0)cos

γ1γ2 t;

A2 (t )= A2max

sin

γ1γ2 t;

A2max

γ2

A1 (0).

5.2

ν ν

(0)

б)

(

а) A0

1 2

;

1 2

;

γ1γ2

ν ν

(

(0)

в) A0

1 2

;

г) A0

1 2

γ1γ2

γ2

γ1γ2

5.3

a) A(t )=

A(0)

(0)

Α(0)

; A

;

t0 = −

ln 1

−

;

(0)

2ν

A(0)

1−

e2νt

A(0)

б) A(t )≈

A(0)

;

A(0) =

;

A(0)

(0)

(t→t0 )

e−

A(0)νt −ln

A(0)

0)− A(0)

A(0)

e−

A(0)

t0 =

A(0)

;

A(0)ν

A(0)− A(0)

(0)

в) A−

≈

≡ A

;

A+

≈

≡ A∞ >> A

4νβ <<1

(0)

e−

A(0)

При

t0 ≈

A(0)

;

A(0)ν

A(0)− A(0)

γ2

(0)

г) Для A(0) >> A(0)

1 ln

A(t) − A

= (A(0) )3 γt +C;

A(0)

(0)

A(t) + A

C =

A(0)

A(0) − A(0)

< 0.

При A(t) → ∞

имеем

A(t) ≈

A(0)

; t0

≈ −

A(0)

(0)

γt

(0)

A(0) + A

)

5.4

γ1,2

−2

(1−ch

−2

λt ).

A1,2,

(t )=

A00

λt;

(t )= A00

6.1

107

Ответы

3kTe0mδ0 (ω2 +ν02 )

ω2

≈ E

;

ђр

;

≈ a

240π

кр

6.2

E (0)

ek0

E (x)=

;

P (x)=

E (

E (0)

E (

1−

+ 1−

6.3

E (0)e−k0

E (x)=

;

P (x)=

E2 (0)

(1−e

−2k

)

E2 (0)

(1−e

−2k

0 )

Ep2

6.4

E2 (0)

4k0

>>1;

E(x) ≈ E(0)e

−k

;

P(x) ≈ e

4E2p

6.5

2 (0)

Δϕ(xz)= −

ω2p0ν02

− E

+ln

E2 Ep2 +1

;

4 c

ω4

Ep2

E2 (0) Ep2 +1

1 ω

ω2p0ν02 E2 (0)

E2 (0)

Δϕ

+ln

+1 .

x→∞

4 c

ω4

Ep2

6.6

ω2p0

Δϕ(xz)=

1 ω

1− E2 E2

4 c

L0 ω4

ln 1− E2 (0)

Ec2 ;

= − 1 ω L0

ω2

(

Δϕ

1−

x→∞

4 c

6.7

ω2p0

(1−e−E2 Ec2 )> 0.

εнл =

ω2

7.1

7.2

108

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1211 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.03.2016409.6 Кб17методичка Судоустрій ч 1.doc
#
23.02.2015721.64 Кб121Методичка Топография.pdf
#
13.03.2016991.74 Кб225МЕТОДИЧКА ФФМ.doc
#
13.03.2016421.89 Кб14методичка Хоз процес 2015 (1).doc
#
01.07.20253.85 Mб0методичка часть 2.doc
#
23.02.20151.52 Mб54методичка черногор.pdf
#
11.11.2019185.34 Кб6Методичка юр.пс..doc
#
01.03.20251.56 Mб0Методичка- Фіноблік.doc
#
23.02.2015783.36 Кб455Методичка-модуль №1 СМ 121 стр.doc
#
23.02.20151.77 Mб52Методичка. Кластерный анализ_пошагово.docx
#
13.03.2016737.73 Кб57Методичка. Лаврик. Основи журналістики.pdf