Тензорная функция Грина, Яцук

ОСНОВЫ МЕТОДИКИ РЕШЕНИЯ ЗАДАЧ ИЗЛУЧЕНИЯ И РАССЕЯНИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН.

Следует учесть, что задача электродинамики, как правило, сводится к решению уравнений, вытекающих из однородных и неоднородных уравнений Максвелла. Отыскание собственных колебаний в системе связано с решением однородных уравнений, задачах излучения и рассеяния электромагнитных волн приходится иметь дело с неоднородными уравнениями, в которых фигурируют источники поля в виде функций распределения плотности электрического и

магнитного токов j э и j M . Для определения искомого поля в общем случае надо решать шесть связанных дифференциальных уравнений в частных производных относительно шести компонент электрического и магнитного поля. Эта сложная задача упрощается введением вспомогательных

электрического и магнитных полей Ε и Η находят с помощью электрического вектора Герца Πэ:

Ε = graddivΠэ + k 2Πэ;

(2)

H = iωεrotΠэ.

Если поле возбуждается магнитным током, для определения векторов Ε и Η используют магнитный вектор Герца ΠM :

Η = graddivΠM + k 2ΠM ;

(3)

Ε= iωεrotΠM .

Вобщих случаях для определения полей Ε и Η необходимо сначала решить уравнение (1).

2

Необходимо отметить, что в ряде случаев (например, при решении двумерных задач, когда вариация поля по одной из координат равна нулю) уравнения Максвелла могут быть сведены к скалярному уравнению Гельмгольца относительно одной из компонент поля, с помощью которой могут быть найдены остальные компоненты. Запишем это уравнение относительно некоторой скалярной функции ψ (r ) в виде

где ρ(r )- известная функция, однозначно связанная с плотностью источника

поля. От векторного уравнения (1) к скалярному (4) можно перейти, если условия задачи позволяют расписать его по компонентам в декартовой системе координат.

Из всего сказанного выше ясно, как важно уметь решать скалярные и векторные уравнения Гельмгольца. Одним из наиболее эффективных методов решения неоднородного уравнения Гельмгольца является метод функции Грина. Теория функции Грина систематически изложена в монографии [1] и ряде советских и зарубежных авторов [2-5].

Вопросы и упражнения.

1.Какие вспомогательные векторы вводятся для упрощения решения уравнений Максвелла, каким уравнением они удовлетворяют?

2.Как выражается поле Ε и Η с помощью электрического и магнитного векторов Герца?

3.Какой метод чаще всего используется для решения неоднородного уравнения Гельмгольца?

4.Распишите по компонентам векторное уравнение Гельмгольца в декартовой системе координат

СВОЙСТВА ФУНКЦИИ ГРИНА

В соответствии с определением, данным в [1], функция Грина является ядром интегрального оператора, преобразующего в решение плотность распределения внешних источников и (или) граничные условия. Если источники и решения являются скалярными функциями, то функция Грина – тоже скаляр. Если рассматриваются векторное поле и породивший его векторный источник, то функция Грина должна быть тензором, поскольку именно тензор преобразует один вектор в другой.

3

Свойства скалярной функции Грина

1.Скалярная функция Грина (обозначим ее G (rr′) удовлетворяет

такому уравнению:

где δ (r −r′) - дельта-функция Дирака, r и r′– радиусывекторы двух точек.

Физический смысл функции Грина следует из самого вида уравнения (5), которое получается из (4), если в последнем в качестве функции распределения плотности источника везде равна нулю, за исключением единственной точки r = r′, где она образуется в бесконечность. Следовательно, G (rr′) есть поле в точке r , возбужденной точечным источником, расположенным в точке r′.

2.Функция Грина инвариантна относительно взаимной замены

координатr и r′,

производная первого порядка здесь терпит разрыв первого рода.

Свойства тензорной функции Грина

1. Тензорная функция Грина (обозначим ее G (rr′) удовлетворяет тензорному уравнению Гельмгольца

где I -единичный вектор.

2.Функция G (rr′) – это симметричный тензор второго ранга,

определяемый девятью компонентами. Симметричность тензора обеспечивается выполнение равенства

F (r )G (rr′)=G (r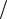r′)F (r ).

4

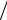
Наличие девяти компонент обусловлено тем, что каждая компонента векторного источника может породить три компоненты поля (3х3=9).

3.Все компоненты тензорной функции Грина G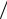 (rr′)

характеризуются также свойствами, определенными в п.2 и 3 для скалярной функции Грина.

4. Самым важным свойством функции Грина, как скалярной, так и тензорной, является то, что с их помощью можно получить решения соответствующих уравнений Гельмгольца.

Вопросы к теме

1.Каким уравнением удовлетворяют скалярная и тензорная функции Грина?

2.Что такое дельта-функция Дирака?

3.Каков физический смысл функции Грина?

4.Какими особенностями характеризуются трехмерная, двумерная и одномерная функции Грина?

ПРЕДСТАВЛЕНИЕ РЕШЕНИЙ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА

СПОМОЩЬЮ ФУНКЦИИ ГРИНА

1.Решение скалярного уравнения (4) в области V , ограниченной замкнутой поверхностью S , может быть представлено в следующем виде:

ψ (r )= ∫ρ(r )G (r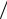r′)dv′+

Здесь индекс S у радиуса– вектораrs′ обозначает, что точка интегрирования

расположена на поверхности S , n – орт внешней нормали к поверхности S . Для получения выражения (7) необходимо было выполнить следующие

операции: уравнение (4) умножить на функцию G (r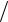r′), уравнение (5)– на

ψ (r ), вычесть полученные равенства одно из другого, произвести взаимную

замену координат r и r′, проинтегрировать результат в объеме V по штрихованным координатам и, воспользовавшись вторым тождеством Грина [1], перейти к полученному выше окончательному результату.

2. Решение векторного уравнения (1) получают аналогичным образом,

5

рассматривая его совместно с уравнением (6). Однако здесь приходится пользоваться не вторым тождеством Грина, а его векторным аналогом [1]. Поэтому окончательный вид решения оказывается несколько более сложным, чем решение (7) скалярного уравнения Гельмгольца:

+41π ∫s {n G (r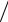rs′)divΠэ(м) (rs′)−nΠэ(м)divG (r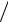rs′)+

+nG (r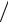rs′) rotΠэ(м) (rs′)− nG (r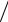rs′) rot G (r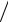rs′)}ds′.

Второе тождество Грина

Упражнение

Проделайте все промежуточные выкладки для получения выражений (7) и (8), пользуясь данными в настоящем разделе методических указаний /пп.1,2/

6

ГРАНИЧНЫЕ УСЛОВИЯ ДЛЯ ФУНКЦИИ ГРИНА Надо подчеркнуть, что как в скалярном, так и векторном случаях,

решение соответствующего уравнения Гельмгольца представляется суммой объемного и поверхностного интегралов. Подынтегральные выражения поверхностных интегралов содержат граничные значения искомой функции и ее производных, которые должны быть заранее известны. Разумеется, это ограничивает круг решаемых задач или существенно усложняет получение решения. Если граничные значения искомой функции заранее не известны, равенства (7) и (8) превращаются, по сути, в интегральные уравнения, решение которых - задача не менее сложная, чем решение искомых дифференциальных уравнений.

От поверхности интегралов в рассматриваемых выражениях можно избавиться, специальным образом подбирая функцию Грина. Если функция Грина удовлетворяет на поверхности S тем же однородным граничным условиям, что и искомая функция, поверхностные интегралы исчезают благодаря тому, что подынтегральные выражения в них обращаются в нуль. Сформируем граничные условия для функций Грина таким образом, чтобы решения уравнений Гельмгольца определялись только Объемными интегралами.

Скалярная функция Грина В случае скалярного уравнения Гельмгольца характер граничных условий

весьма прост: на идеально проходящей поверхности искомая функция, как правило, удовлетворяет однородным граничным условиям Дирихле

(ψ (rs′)= 0) или Неймана (∂ψ (rs′)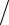∂n = 0). Тем же условиям должна удовлетворять и скалярная функция Грина G (r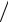rs′)= 0 или ∂G (r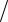rs′)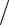∂n = 0.

Тензорная функция Грина В случае векторного уравнения Гельмгольца граничные условия гораздо

сложнее, поскольку их надо формулировать отдельно для тангенциальных и нормальных компонент искомого поля.

Векторные уравнения Гельмгольца (1) записаны относительно электрического и магнитного ве5кторов Грина, которые на идеально проводящей поверхности должны удовлетворять тем же граничным условиям, что и соответственно векторы электрического и магнитного полей. В этом можно убедиться, анализируя выражения (2) и (3),

7

следовательно, для электрического вектора Герца Πэ граничные условия на идеальном металле можно записать в таком виде:

n,Πэ (rs′) = 0; (9) divΠэ (rs′)= 0.

Первое условие очевидно, поскольку оно отражает поведение тангенциальных компонент электрического поля. Второе условие при отсутствии сторонних зарядов и однородном диэлектрическом заполнении области V непосредственно вытекает из материальных уравнений Максвелла.

Граничные условия для магнитного вектора Герца формулируются так:

следовательно, и магнитного вектора Герца, равна нулю. Второе условие требует равенства нулю тангенциальной составляющей электрического поля (см. (3) второе равенство).

Таким образом, для электрической и магнитной функции Грина следует формулировать граничные условия, аналогичные условиям (9) и (10).

Возникает вопрос, каким же образом построить функцию Грина, являющуюся тензором и удовлетворяющую заданным граничным условиям.

Вопросы и упражнения

1.Какова структура решения неоднородного уравнения Гельмгольца, полученного в самом общем виде с помощью функции Грина?.

2.Напишите граничные условия, которым удовлетворяют тангенциальные и нормальные составляющие электрического и магнитного полей на идеально проводящей поверхности.

8

ПРИНЦИП ПОСТРОЕНИЯ ТЕНЗОРНОЙ ФУНКЦИИ ГРИНА И СОБСТВЕННЫЕ ВЕКТОРНЫЕ ФУНКЦИИ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА

1.Метод построения Грина Необходимо знать, что при построении функции Грина для замкнутых

областей правильной формы (когда составные части граничной поверхности совпадают с участками координатных поверхностей) обычно используются метод собственных функций. Тензорную функцию получают путем тензорного перемножения векторов. В качестве перемножаемых векторов используются собственные векторные функции уравнения Гельмгольца и неизвестные векторные коэффициенты разложения.

2. Трехмерные собственные векторные функции Полная система полных векторных функций построена в шести из

известных одиннадцати ортогональных систем координат с разделяющимися переменными: в прямоугольной системе x, y, z трех цилиндрических (круговой, эллиптический и параболический цилиндры сферической и конической [1].

В наиболее употребляемой цилиндрической системе координат вид этих функций таков:

направлен вдоль оси цилиндрической системы (в случае декартовой системы роль z0 могут выполнять также орты x0 и y0 ).

Скалярные функции ϕ(r ),ψ (r )и χ(r ) удовлетворяют идентичным уравнениям Гельмгольца. Запишем одно из них для функции ϕ(r ):

граничными условиями, которым должна удовлетворять собственные векторные функции (11). Последние подчиняются тем же граничным условиям,

9