
Задачи физика модуль
.doc1.1. Основные формулы и соотношения
Уравнение Менделеева-Клапейрона
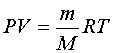 ,
(1.1)
,
(1.1)
где Р –
давление газа; V –
объем газа, m –
масса газа; М –
молекулярная масса газа; ![]() –
универсальная газовая постоянная; Т –
абсолютная температура;
–
универсальная газовая постоянная; Т –
абсолютная температура; 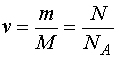 –
количество вещества, гдеN –
число молекул,
–
количество вещества, гдеN –
число молекул, ![]() –
постоянная Авогадро.
–
постоянная Авогадро.
Закон Дальтона
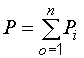 ,
(1.2)
,
(1.2)
где Р –
давление смеси газов, ![]() –
парциальное давление составляющих
смесь.
–
парциальное давление составляющих
смесь.
Плотность газа
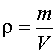 ,
(1.3)
,
(1.3)
где m – масса газа, V – объем газа.
Давление газа
![]() ,
(1.4)
,
(1.4)
где 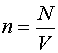 –
концентрация молекул,
–
концентрация молекул, ![]() –
постоянная Больцмана.
–
постоянная Больцмана.
Кинетическая энергия одной молекулы:
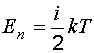 ,
(1.5)
,
(1.5)
где i – число степеней свободы.
1.2. Примеры решения задач
Задача 1. Определить плотность смеси газов водорода массой 8 г и кислорода массой 64 г при температуре 290 К и давлении 0,1 МПа. Газы считать идеальными.
|
|
Решение. Плотность газа определяется
где масса смеси определяется их суммой:
|
Количество вещества смеси:
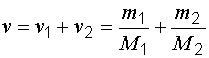 .
(1.7)
.
(1.7)
Уравнение Менделеева-Клапейрона для смеси газов:
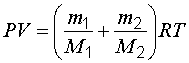 .
(1.8)
.
(1.8)
Определим объем смеси газов из уравнения (1.8):
 ,
(1.9)
,
(1.9)
Подставив в формулу (1.6) значение объема (1.9), получим:
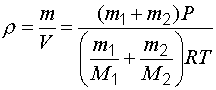 .
(1.10)
.
(1.10)
Проверим размерность:
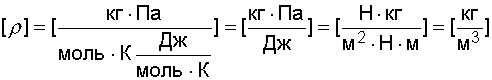 .
.
Произведем вычисления:
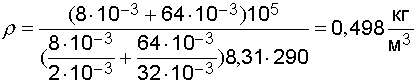 .
.
Ответ:
плотность смеси ![]() .
.
Задача 2. В сосуде вместимостью 0,3 л при температуре 290 К находится некоторый газ. На сколько понизится давление газа в сосуде, если из него в результате утечки выйдет 1019 молекул?
|
|
Решение. Запишем уравнение Менделеева-Клапейрона для двух состояний газа
|
Определим давление газа в первом и во втором состояниях:
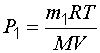 и
и 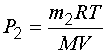 .
(1.12)
.
(1.12)
Изменение давления
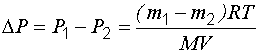 .
(1.13)
.
(1.13)
Число молекул, покинувших сосуд:
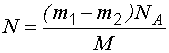 .
(1.14)
.
(1.14)
Следовательно, 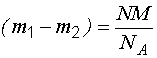 ,
подставив это значение в формулу
изменения давления, получим:
,
подставив это значение в формулу
изменения давления, получим:
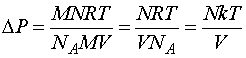 .
.
Проверим размерность:
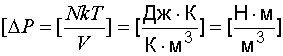 =
[Па].
=
[Па].
Произведем вычисления:
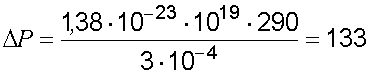 (Па).
(Па).
Ответ: давление газа понизилось на 133 Па.
Задача 3. В баллоне объемом 10 л находится гелий под давлением 1 МПа при температуре 300 К. После того как из баллона было израсходовано 10 г гелия, температура понизилась до 290 К. Определить давление гелия, оставшегося в баллоне.
|
|
Решение. Запишем уравнение Менделеева-Клапейрона для первого и второго состояний газа:
Выразим массу газа в первом и во втором состояниях: |
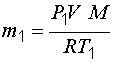 и
и 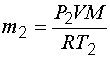 .
(1.17)
.
(1.17)
Масса израсходованного гелия:
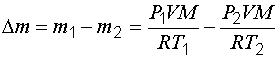 ,
(1.18)
,
(1.18)
Из этого уравнения выразим искомое давление:
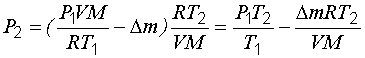 .
(1.19)
.
(1.19)
Проверим размерность:
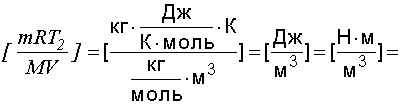 [Па].
[Па].
Произведем вычисления:
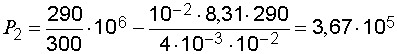 (Па).
(Па).
Ответ:
давление газа оставшегося в сосуде
равно ![]() Па.
Па.
Задача 4. Найти среднюю кинетическую энергию одной молекулы аммиака NH3 при температуре 27 оС и среднюю энергию вращательного движения одной молекулы при той же температуре.
|
|
Решение. Полная средняя энергия одной молекулы определяется по формуле |
где i – число степеней свободы, k – постоянная Больцмана, Т – термодинамическая температура.
Для четырех атомных молекул полное число степеней свободы равно 6, из них 3 поступательного и 3 вращательного движения.
Средняя энергия вращательного движения молекулы определится по формуле
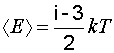 ,
(1.21)
,
(1.21)
Проверим размерность:
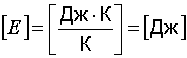 .
.
Подставим значения величин в формулы (1.20), (1.21) и вычислим энергии
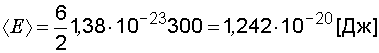 ;
;
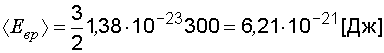 .
.
Ответ:
полная энергия молекулы 1,242![]() 10-20 Дж,
энергия вращательного движения молекулы
6,21
10-20 Дж,
энергия вращательного движения молекулы
6,21![]() 10-21 Дж.
10-21 Дж.

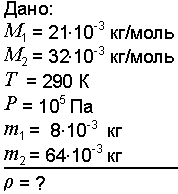
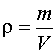 ,
(1.6)
,
(1.6)
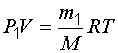 ,
, 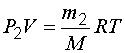 .
(1.11)
.
(1.11)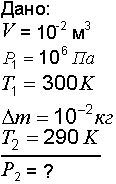
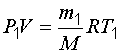 и
и 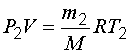 .
(1.16)
.
(1.16)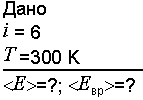
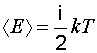 ,
(1.20)
,
(1.20)