2013 / УказНаФункцЛекция_4

Лекция 4.

Указатель на функцию.

Указатель на функцию содержит адрес оперативной памяти, по которому располагается исполняемый код функции, т.е. адрес, по которому передаётся управление при вызове функции. Указатель на функцию используется:

• для косвенного вызова функции (т.е. не через её имя, а через обращение к переменной, хранящей её адрес);

• для передачи имени функции в другую функцию.

Указатель функции имеет тип “указатель функции, возвращающей значение заданного типа и имеющей аргументы заданных типов”. Эта информация задаётся при описании указателя функции:

Тип (* имя_указателя) (список типов аргументов);

где

Тип - тип рез-та функции;

имя_указателя – имя указателя функции;

в списке типов аргументов перечисляются типы через запятую.

Пример: int (*pf) (double, double);-

задаёт указатель с именем pf на функцию, возвращающую значение типа int и имеющую два аргумента типа double.

Если есть функция с такими характеристиками, например:

int f (double a, double b) { /* тело функции*/ }

можно указателю pf присвоить имя функции pf=f; или pf=&f;

После этого можно вызвать функцию f()

как через имя функции: cout<<f (3.2, 2.5);

так и через указатель: cout<<pf (3.2, 2.5);

или cout<<(*pf) (3.2, 2.5);

Часто, чтобы сделать программу легко читаемой используют переименование типов ( программист даёт новое имя типу).

typedef тип новое_имя [размер];

//в [] необязательная часть.

Можно описать тип указателя на функцию с заданным типом результата и заданными типами параметров.

typedef тип_результата (*тип-указателя) (список типов параметров) ;

Можно описать, например, тип TF как тип указателя на функцию с двумя параметрами типа double и результатом типа int:

typedef int (*TF) (double, double);

Если определён тип указателя на функцию, его можно использовать:

• определить переменную этого типа; например:

TF qf;

Этой переменной можно присвоить значение qf=f; либо qf=&f;

и обращаться к этой функции через указатель qf.

• этот тип указателя можно использовать для описания параметра функции, т.е. в некоторую функцию можно передать как параметр другую функцию, описав этот параметр с типом указателя, например:

void NN (int a, int b, TF w)

{double x, y;……int z= w (x, y);…}

Рассмотрим некоторые примеры функций, в которые передаются имена других функций.

Некоторые итерационные методы решения уравнений f(x)=0

Корнем уравнения f(x) =0 называют такое значение x=ξ, что f (ξ)=0.

I этап. Отделение корней: Найти такой отрезок [α,β], на котором определены и непрерывны функции f(x), f’(x), f’’(x) и лежит один и только один корень уравнения. Достаточные условия этого:

• f(α)* f(β)<0;

• f’(x) на [α,β] сохраняет знак.

II этап. Уточнение корня. Найти приближённое значение корня с заданной точностью ε.

Некоторые методы уточнения корня:

I. Метод деления отрезка пополам.

1. t= f(α); значение функции на левом конце отрезка.

2. xc=( α+β)/2; середина отрезка [α,β].

3. Пока |α - β|>= ε выполнять

{r =f (xc); значение функции в средней точке.

Если (r * t>0) //r и t одного знака

то α=xc; выбираем правую половину отрезка

иначе β=xc; выбираем левую половину отрезка

xc=( α+β)/2; новая середина отрезка [α,β].

}

4. т.к. |α - β|< ε, то середина xc- корень с точностью ε.

II. Метод касательных.

Строится последовательность приближений к корню

x₀ , x₁ , x₂ ,. . . x_n-1 , x_n , x_{n+1 ,. . . .,}

Где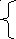

x₀ = α, если f(α) *f’’(α)>0

β, в противном случае

последовательность строится по формуле:

x _n+1 = x _n– f(x_n) / f’ (x_n)

Условие окончания: |x_n+1- x_n|< ε;

III. Метод хорд.

Строится последовательность приближений к корню

x₀ , x₁ , x₂ ,. . . x_n-1 , x_n , x_{n+1 , . . . . . .}

Где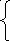

x₀= α, если f(α)*f’’(α)<0

β, в противном случае

последовательность строится по формуле:

x_n+1=x_n – _* f(x_n)

Условие окончания: |x_n+1- x_n|< ε;

Пример 1. Написать функцию для решения уравнения f(x)=0 методом касательных. Уравнение e^-x-x = 0.

Требуется определить две функции для f (x) и f ’(x).

#include <iostream>

#include <cmath>

using namespace std;

double f (double x) {return exp(-x)-x;}

// значение функции f(x)

double f1(double x) {return (-exp(-x)-1); }

//значение производной f’(x)

typedef double (*TF) (double);

//TF тип указателя на функцию типа f и f1

double mettang (double x0, double eps, TF pf, TF pf1)

{ double x1, x2=x0;

do

{x1=x2;

x2=x1 – pf(x1)/ pf1(x1);

}while (fabs (x1- x2)>=eps);

return x2;

}

int main()

{ double x0,eps;

cout<<”--> x0, eps\n”;

cin>> x0>> eps;

cout<<”корень=”<< mettang (x0, eps, f, f1) << ’\n’;

return 0;

}

Пример 2. Вычислить приближённое значение определённого интеграла на заданном отрезке [a,b] от задаваемой функции f(x). Есть несколько способов:

a)Отрезок интегрирования [a,b] разбивается на N равных частей, шаг деления h=(b-a)/N, на каждом отрезке площадь заменяют прямоугольником с высотой, равной значению функции на левом, правом конце, либо трапецией с основаниями – значениями функции на концах, либо объединяют по два отрезка и заменяют кусочек функции параболой на этих отрезках. Соответственно получают формулы левых, правых прямоугольников, трапеций и парабол (Симпсона):

J(a,b,N,f(x))_{левых пр}.= h*(f(a)+f(a+h)+ f(a+2*h)+……+f(a+(N-1)*h))

J(a,b,N,f(x))_{правых пр}.= h*(f(a+h)+f(a+2*h)+ ……+f(a+(N-1)*h)+f(b))

J(a,b,N,f(x))_{трапеций}= h/2*(f(a)+2*f(a+h)+ ……+2*f(a+(N-1)*h)+f(b))

J(a,b,N,f(x))_{парабол}= h/3* (f(a)+4*f(a+h)+2*f(a+2*h) +4*f(a+3*h)

+2*f(a+4*h)+ ……+4*f(a+(N-1)*h)+f(b))

Значение интеграла получается с некоторой точностью, для достаточно гладкой функции f(x) этой точности часто хватает, если нет - можно увеличить N.

b)Задачу можно поставить и так: вычислить с заданной точностью eps приближённое значение интеграла на заданном отрезке [a,b] от задаваемой функции f(x). В этом случае строят последовательность приближённых значений интеграла, пока два соседние приближения не станут близки: |J_n+1-J_n |<eps.

Последовательные значения интеграла получаются по выбранной формуле для делений отрезка интегрирования на N, 2*N, 4*N,и т.д.

частей. В теории доказано, что для достаточно гладкой подинтегральной функции так построенная последовательность будет сходиться. Однако здесь есть одна особенность: увеличение точек деления отрезка каждый раз в 2 раза приводит к тому, что в новом делении присутствуют старые и новые точки деления, при вычислении очередной суммы значений подинтегральной функции это надо учитывать и вычислять её без пересчёта значений в старых точках. Это не сложно для формул левых, правых прямоугольников, трапеций, несколько сложнее для формулы парабол.

Рассмотрим формулу трапеций.

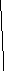
У

a a+h a+2h a+3h b X

h=(b-a)/N;

I_N= h/2*(f(a)+f(b)+2*S); //S-сумма значений в средних точках

N1=2*N; h1=h/2;

I_2N= h1/2*(f(a)+f(b)+2*(S+S’));//S’-сумма значений в новых точках

Поэтому новое приближение I_2N надо вычислять так:

I_2N = I_N/2+ S'*h1; //без пересчёта значений в старых точках.

Для формулы Симпсона (N- чётное):

I_N =h/3*(f(a)+4*f(a+h)+2*f(a+2*h) +

+4*f(a+3*h)+2*f(a+4*h)+ ……+4*f(a+(N-1)*h)+f(b))=

=S0 + 4*S1 + 2*S2;

где S0= h/3*(f(a)+f(b));

S1= h/3*(f(a+h)+f(a+3*h)+……f(a+(N-1)*h));

//сумма в ”нечётных” точках.

S2= h/3*(f(a+2*h)+f(a+4*h)+……f(a+(N-2)*h));

//сумма в ”чётных” точках.

N1=2*N; h1=h/2;

Для вычисления I_2N надо пересчитать S0, S1, S2.

S0^нов= S0/2 ; S2^нов=(S1+S2)/2; //все точки старые.

S1^нов=h1/3*(f(a+h1)+f(a+h1+h)+f(a+h1+2*h)+…+f(a+h1+2*(N1-1)*h)) //здесь все новые точки.

I_2N =S0 ^нов +4* S1^нов +2* S2^нов ;

Пример программы для a)

#include <iostream>

using namespace std;

double f(double x)

{return x*x;}

//можно не опиcывать тип указателя на функцию

double metparabol(double a,double b,int n, double(*tf)(double))

{double h,x,s,e;

int k;

h=(b-a)/n;

s=h/3*(tf(a)+tf(b));

k=4; x=a+h; e=b-h/2;

while (x<e)

{s=s+k*tf(x)*h/3;

x=x+h; k=6-k;

}

return s;

}

int main ()

{double a,b;

int n;

cout<<"vvedite a,b,n \n";

cin>>a>>b>>n;

cout<< metparabol(a,b,n,f)<<endl;

return 0; }