
Кислов. атомная физика
.pdf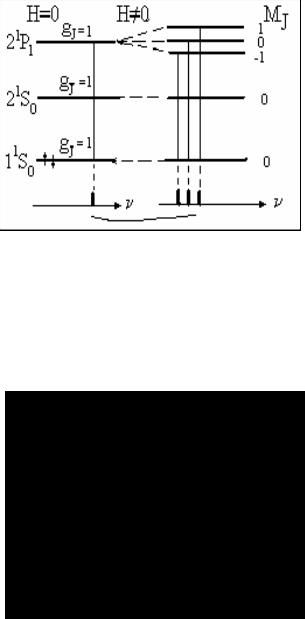
Кислов А.Н. |
|
Атомная физика |
|
где g J =1 + |
J (J +1) + S(S +1) − L(L +1) |
; MJ = –J,…,J. Таким образом, в |
|
2J (J +1) |
|||
|
|
магнитном поле снимается вырождение по квантовому числу MJ и появляются (2J + 1) зеемановских подуровня. Расстояние ∆Е между соседними зеемановскими подуровнями различно:
∆E = g J µb H = g J ωл .
Оно зависит от фактора Ланде g J , значение которого определяется кванто-
выми числами L, S и J. Расщепление уровней таким способом приводит к аномальному эффекту Зеемана.
Рассмотрим этот эффект на примере спектральных линий атома натрия Na, которые называются желтым дублетом. Он образуется при квантовых переходах между энергетически-
ми уровнями ЕnJ тонкой структуры
32Р1/2→32S1/2 и 32Р3/2→32S1/2, изобра-
женных на рис. 7.4. В магнитном поле вместо первой спектральной линии желтого дублета появятся четыре линии, а вместо второй линии шесть линий. Это нетрудно показать, учитывая
Рис. 7.4 правила отбора для квантовых чисел
(7.16).
Если у атома квантовое число S равно нулю (S = 0), т.е. спин S = 0, тогда J = L. Согласно (7.17), каждый энергетический уровень расщепляется на (2L + 1) зеемановских подуровня. Причем, расстояние ∆Е между соседними зеемановскими подуровнями одинаково:
|
|
∆E = µb H = ωл |
, |
|
|
|
так как g J = 1. При таком расщепле- |
||||
|
нии наблюдается нормальный эф- |
||||
|
фект Зеемана. |
|
|
||
|
Проявление этого эффекта рас- |
||||
|
смотрим |
на примере спектральной |
|||
|
линии атома парагелия, т.е. атома ге- |
||||
|
лия 2He, у которого спин |
S = 0, ос- |
|||
|
новное состояние 11S0 и имеются |
||||
Рис. 7.5 |
только |
синглетные |
состояния |
||
(рис. 7.5). В магнитном поле вместо |
|||||
|
|||||
одной спектральной линии появятся три линии. |
|
|
|
||
|
|
|
|
||
ГОУ ВПО УГТУ-УПИ − 2005 |
|
Стр. 121 из 142 |
|||

Кислов А.Н. Атомная физика
Сейчас рассмотрим действие сильного магнитного поля. Этот предельный случай объясняет эффект Пашена – Бака. Сильным магнитное поле называется, если зеемановское расщепление, вызываемое полем, превышает расщепление, связанное со спин-орбитальным взаимодействием, т. е.
UH >> USL. В этом случае взаимодействие векторов L и S атома с полем больше их взаимодействия между собой, поэтому не имеет смысла рассмат-
ривать вектор J , поскольку векторы L и S ведут себя независимо друг от друга. Следовательно,
U H = −(µLz + µSz )H .
Причем состояние атома описывается волновой функцией ΨnLM LM S с кван-
товыми числами n, L, ML, MS, поэтому значение энергетического уровня атома вычисляется следующим образом:
EnLM LM S = EnL + U H = EnL − ∫ΨnLM* |
LM S (µLz + µSz )HΨnLM LM S dV = |
V |
|
= EnL + (M L + 2M S )µb H , |
|
где ML = –L,…,L; MS = –S,…,S. В магнитном поле снимается вырождение по квантовым числам ML и MS и появляются дополнительные подуровни. Такое расщепление объясняет эффект Пашена – Бака.
Рис. 7.6
Рассмотрим данный эффект на примере спектральной линии атома натрия Na, которая образуется при квантовом переходе 32Р→32S между уровнями ЕnL (рис. 7.6). Учитывая правила отбора для квантовых чисел (7.16), можно показать, что в магнитном поле вместо одной спектральной линии появятся три линии.
ГОУ ВПО УГТУ-УПИ − 2005 |
Стр. 122 из 142 |

Кислов А.Н. |
Атомная физика |
Глава 8. Молекулярные спектры
8.1. Особенности молекулярных спектров. Квантование колебательных и вращательных уровней
В предыдущих главах рассматривались изолированные атомы и связанные с ними явления. Перейдем теперь к рассмотрению более сложных систем, а именно молекул, состоящих из множества атомов. В молекуле наряду с движением электронов в атомных оболочках происходит изменение положения самих атомов относительно друг друга и изменение ориентации молекулы в пространстве как целого. Таким образом, существует электронное, колебательное и вращательное движение молекулы, или, другими словами, молекула обладает электронными, колебательными и вращательными степенями свободы. В связи с этим, если пренебречь взаимодействием различных видов движения друг с другом и не учитывать поступательное движение молекулы, то полную энергию Ei молекулы, находящейся в i-м стационарном состоянии, можно представить в виде суммы энергий электронного Ei,эл, колебательного Ei,кол и вращательного Ei,вр движений:
Ei = Ei,эл + Ei,кол + Ei,вр .
Значения полной энергии Ei молекулы могут быть определены в рамках квантовой механики. Квантово-механические расчеты показывают, что все вклады в энергию Ei молекулы являются квантованными величинами. Причем квантование электронного вклада Eэл было рассмотрено в гл. 5. Экспериментально установлено, что электронная энергия Eэл молекулы примерно в 10 ÷ 100 раз превышает энергию ее колебательного движения Eкол. Последняя, в свою очередь, в 100 ÷ 1000 раз превышает энергию вращательного движения
Eвр:
|
|
Eэл >> Eкол >> Eвр . |
|
|
|
Это означает, что каждому элек- |
|
|
|
тронному уровню определенного |
|
|
|
стационарного состояния отвечает |
|
|
|
своя система колебательных уров- |
|
|
|
ней, а каждому колебательному |
|
|
|
уровню своя система вращатель- |
|
|
|
ных уровней (рис. 8.1). Такая сис- |
|
|
|
тема энергетических уровней при- |
|
|
Рис. 8.1 |
водит к сложной структуре моле- |
|
|
кулярных спектров излучения или |
||
|
|
|
|
ГОУ ВПО УГТУ-УПИ − 2005 |
Стр. 123 из 142 |
||

Кислов А.Н. |
Атомная физика |
поглощения. Частота ν спектральной линии в таких спектрах определяется из формулы
hν = ∆Eэл + ∆Eкол + ∆Eвр .
В отличие от атомных линейчатых спектров молекулярные спектры называются полосатыми и представляют собой систему близко расположенных полос, каждая из которых состоит из группы спектральных линий.
Рассмотрим на примере двухатомной молекулы с массой атомов М1 и М2
ирасстоянием между атомами, равным r, как квантуются колебательная Eкол
ивращательная Eвр энергии.
Для определения значений колебательных уровней Ei,кол i-го стационарного состояния молекулы необходимо решить стационарное уравнение Шредингера
∆Ψi + 2µ2 (Ei,кол −Ui )Ψi = 0 ,
где µ = |
M1M 2 |
|
– приведенная масса; Ψi – волновая функция, описываю- |
||
M1 |
+ M |
2 |
|||
|
|
||||
щая i-е состояние молекулы; Ui – потенциальная энергия молекулы в i-м состоянии, роль которой играет полная энергия электронов Ei,эл в этом состоянии: Ui = Ei,эл. Вследствие того, что электронная энергия Ei,эл зависит от расстояния между атомами r, необходимо ввести понятие о кривых потенциальной энергии U(r) молекулы (рис. 8.2). Вопрос об аналитическом виде кривых U(r) для конкретных молекул достаточно сложен. Рассмотрим его в общем виде.
Между атомами молекулы действуют силы притяжения и отталкивания. Если под действием этих сил между атомами образуется химическая связь и молекула становится устойчивой системой, то кривая потенциальной энергии U(r) будет обладать минимумом в точке r = ro, где ro – это равновесное положение атомов.
Рассмотрим случай малых колебаний атомов молекулы, т.е. их малых смещений u = r – ro от положения устойчивого равнове-
ГОУ ВПО УГТУ-УПИ − 2005 |
Стр. 124 из 142 |

Кислов А.Н. |
Атомная физика |
сия. Тогда в разложении потенциальной энергии U(r) (электронной энергии Eэл) в ряд Тейлора около точки равновесия ro по степеням смещений u можно ограничится вторым порядком малости:
|
U (r) ≈U (r |
) + |
dU |
|
|
|
u + |
1 |
|
d 2U |
|
|
|
|
|
|
u 2 |
, |
(8.1) |
|||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
o |
|
dr |
|
ro |
|
|
2 dr 2 |
|
|
ro |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
где U (r |
) – постоянная величина. Причем |
|
dU |
|
|
= 0 , так как U (r |
) является |
|||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
o |
|
|
|
|
|
|
|
dr |
|
ro |
|
|
|
|
|
|
|
|
o |
|||
|
|
|
|
|
|
|
|
d 2U |
|
|
|
|
|
|
||||||||
минимумом кривой U (r). Введя обозначение k = |
|
|
|
r , которое называется |
||||||||||||||||||
|
|
|
||||||||||||||||||||
dr2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
силовой постоянной, видим, что кривая U (r) аппроксимируется функцией параболического вида:
U (r) =U (r |
) + |
ku |
2 |
. |
(8.2) |
|
|
||||
o |
|
2 |
|
|
|
|
|
|
|
|
=U (u)
Подчеркнем, что второе слагаемое U (u) в этом выражении описывает вклад гармонического колебательного движения в потенциальную энергию U (r)
молекулы.
Из формулы (8.2) следует, что в случае малых колебаний:
1)на атом со стороны другого атома действует сила F= – k u , называемая квазиупругой;
2)при таком характере сил атомы в молекуле будут совершать гармонические колебания около общего центра тяжести, т.е. колебания молекулы происходят по закону гармонического осциллятора. При этом смещения u вы-
числяются по формуле u = uo cos 2πνколt , где uo – амплитуда, νкол = |
1 |
k |
– |
|
2π |
µ |
|
линейная собственная частота колебаний.
Решая стационарное уравнение Шредингера с потенциальной энергией U (r) вида (8.2) (этот случай называется гармоническим приближением),
приходим к следующему выражению для энергии Eкол колебательного движения:
Eкол |
= (v + |
1 |
)hνкол , |
(8.3) |
|
2 |
|||||
|
|
|
|
где v – колебательное квантовое число, принимающее значения v = 0,1,2,… Из формулы (8.3) видно, что колебательная энергия Eкол является квантованной величиной, а колебательные уровни представляют собой систему равно-
ГОУ ВПО УГТУ-УПИ − 2005 |
Стр. 125 из 142 |

Кислов А.Н. |
Атомная физика |
отстоящих уровней (рис. 8.2). Собственной частотой νкол колебаний называ-
ют частоту, соответствующую квантовому переходу между соседними колебательными уровнями. Правило отбора в гармоническом приближении для квантового числа v следующее: ∆v = ± 1.
Колебания молекулы с большими амплитудами уже нельзя аппроксимировать колебаниями гармонического осциллятора. В этом случае колебания являются ангармоническими, а колебательные уровни не будут равноотстоящими. Правило отбора для квантового числа v будет таким: ∆v = ± 2, ± 3,… .
Для определения значений вращательных уровней Eвр стационарного состояния молекулы рассмотрим ее как жесткий ротатор с расстоянием ro между атомами, который вращается вокруг центра тяжести. Тогда кинетическая
энергия вращения Eвр зависит от момента инерции Iim = µro2 молекулы относительно оси вращения и угловой скорости вращения Ω:
Eвр = |
I |
im |
Ω2 |
. |
(8.4) |
|
2 |
||||
|
|
|
|
||
Учитывая, что момент количества движения ротатора Jр
J p = IimΩ ,
для энергии Eвр получаем формулу |
|
|
Eвр = |
J 2p |
|
|
. |
|
2Iim |
||
Поскольку величина Jр квантуется: |
|
|
J p =  J в (J в +1) ,
J в (J в +1) ,
где Jв – вращательное квантовое число: Jв = 0, 1, 2,… , то и Eвр является квантованной величиной:
Eвр = |
2 |
J в (J в +1) . |
(8.5) |
|
|||
|
|||
|
2Iim |
|
|
Согласно формуле (8.5), вращательные уровни – это система неравноотстоящих уровней, у которых расстояние между соседними уровнями возрастает при увеличении квантового числа Jв (рис. 8.2). Правило отбора для квантового числа Jв имеет вид ∆Jв = ± 1.
ГОУ ВПО УГТУ-УПИ − 2005 |
Стр. 126 из 142 |

Кислов А.Н. |
Атомная физика |
8.2. ИК-спектры поглощения
Изменение состояния молекулы подразумевает изменение ее электронного, колебательного и вращательного движения. Этим изменениям соответствуют квантовые переходы между определенными энергетическими уровнями. Если при взаимодействии молекулы с электромагнитным полем происходят переходы на более высокие энергетические уровни, т.е. энергия молекулы повышается, то такие переходы определяют структуру спектра поглощения.
Спектры поглощения, связанные с изменением электронных состояний, рассматривались при изучении теории строения атома (см. гл. 7). Отметим, что эти спектры находятся в области коротковолновых электромагнитных волн (10-4÷10-6 см), а особенности электронного движения объясняются только в рамках квантовой механики. Спектры поглощения, обусловленные колебательным или вращательным движениеми, лежат в длинноволновой инфракрасной (ИК) области электромагнитных волн (10-2÷10-4 см) и называются ИК-спектрами поглощения. Благодаря тому, что волновые свойства у длинноволнового излучения проявляются сильнее, чем у коротковолнового, ряд особенностей колебательного и вращательного движения можно объяснить как на основе классической волновой, так и квантовой теорий взаимодействия света с веществом.
В качестве примера рассмотрим колебательные ИК-спектры поглощения. С квантовой точки зрения возникновение спектральной линии в ИКспектре поглощения объясняется следующим образом. При взаимодействии молекулы с квантом падающего на нее света с частотой ν, равной собственной частоте νкол колебаний молекулы, она изменит свое состояние. Причем молекула поглотит падающий квант, и ее энергия увеличится на величину, равную энергии падающего кванта hνкол. В результате этого в ИКспектре поглощения на частоте νкол
Рис. 8.3 появится спектральная линия
(рис.8.3).
Сейчас для объяснения особенностей в ИК-спектре поглощения обратимся к классическому подходу. При этом для простоты рассмотрим двухатомную молекулу. Согласно классической электромагнитной теории, поглощение электромагнитной энергии, как и ее излучение, связано с движущимися зарядами. Интенсивность поглощения In прямо пропорциональна по-
ГОУ ВПО УГТУ-УПИ − 2005 |
Стр. 127 из 142 |

Кислов А.Н. |
Атомная физика |
току энергии Ф, поглощаемой молекулой, который, в свою очередь, зависит от изменения ее электрического дипольного момента d :
In ~Ф(t) = |
2 |
|
|
d |
|
2 |
|
|
|
|
|
||||||
|
|
|
. |
(8.6) |
||||
3c3 |
||||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Величина электрического дипольного момента d является функцией расстояния r между атомами молекулы, поэтому ее можно разложить в ряд Тейлора около точки равновесного положения атомов rо по степеням смещений u = r – rо, которые в случае их малых значений изменяются по закону гармонических колебаний u = uo cos 2πνколt (гармоническое приближение).
Если при разложении ограничиться первыми двумя слагаемыми, то верно следующее равенство:
d(r) ≈ d(r )+ |
d(d) |
|
|
|
u = d(r )+ |
d(d) |
|
|
|
|
|
||||||||
o |
dr |
|
r |
o |
dr |
|
r |
||
|
|
|
|
||||||
|
|
|
|
o |
|
|
|
|
o |
uo cos 2πνколt .
Таким образом, в гармоническом приближении величина электрического
дипольного момента d молекулы представляет собой сумму двух членов, первый их которых не зависит от времени t, а второй периодически изменяется со временем с частотой νкол и вызывает появление на этой частоте основной (фундаментальной) линии в ИК-спектре поглощения. Ее интенсивность In, как следует из выражения (8.6), прямо пропорциональна квадрату первой производной электрического дипольного момента по межатомному расстоянию r:
d(d) |
2 |
|||
In ~ |
|
. |
||
dr |
||||
|
|
|
||
Итак, в ИК-спектре поглощения наблюдается основная спектральная линия, когда отлична от нуля первая производная электрического дипольного момента по межатомному расстоянию r, имеющая размерность заряда и называемая эффективным зарядом молекулы.
Например, у ионных (гетерополярных) молекул HCl, HBr и т.д. электрический дипольный момент не равен нулю, поэтому у них можно измерять ИК-спектры поглощения. У ковалентных (гомеополярных) симметричных молекул H2, O2 и т.д. электрический дипольный момент отсутствует, следовательно, они не поглощают излучение в ИК-области.
ГОУ ВПО УГТУ-УПИ − 2005 |
Стр. 128 из 142 |
Кислов А.Н. |
Атомная физика |
8.3. Комбинационное рассеяние света
Колебательное движение атомов молекулы при ее взаимодействии с электромагнитными волнами ответственно не только за поглощение электромагнитных волн в ИК-области, но и за их рассеяние. Это явление называется комбинационным рассеянием света. Оно было открыто в 1928 г. Мандельштамом и Ландсбергом в кристаллах и одновременно Раманом в жидкостях. Суть явления состоит в том, что любое вещество может рассеивать падающее на него излучение, при этом в спектре рассеянного света кроме спектральной линии с частотой, совпадающей с частотой νo падающего света
(обычно принадлежит видимой или ультрафиолетовой области), по обе стороны от нее наблюдаются добавочные симметрично расположенные линии с
частотами νc = νo − νкол и νac = νo + νкол, называемые спутниками (с – стоксовые (или красные) и ас – антистоксовые (или фиолетовые)), где νкол – собственные частоты колебаний атомов молекулы.
Некоторые закономерности комбинационного рассеяния света, например происхождение спутников, можно объяснить, основываясь на принципах классической электродинамики. Частота νo падающей на молекулу электро-
магнитной световой волны обычно на несколько порядков больше частоты νкол колебаний атомов молекулы, поэтому атомы почти не чувствуют па-
дающего света. Периодическое электрическое поле |
с напряженностью |
E(t) = Eo cos 2πνot падающей электромагнитной волны |
воздействует на лег- |
кие электроны, которые под влиянием периодической силы, действующей на них, совершают вынужденные колебания. И этот процесс вызывает вторичное излучение, определяющее рассеяние.
Согласно классической электродинамике, интенсивность Ip рассеянного света прямо пропорциональна квадрату модуля второй производной по времени от наведенного падающим светом электрического дипольного момента
молекулы d :
I p ~ |
2 |
|
|
d |
|
2 |
|
|
|
|
|
||||
|
|
|
, |
(8.7) |
|||
3c3 |
|
|
|||||
|
|
|
|
|
|
||
|
|
|
|
|
|||
В свою очередь, электрический дипольный момент d , индуцируемый электромагнитной волной, пропорционален напряженности E(t) электрической составляющей волны с коэффициентом пропорциональности α :
d = αE(t) = α(r)Eo cos 2πνot ( в СГСЭ) , |
|
d = εo αE(t) , εo – электрическая постоянная |
(в CИ) . |
|
|
ГОУ ВПО УГТУ-УПИ − 2005 |
Стр. 129 из 142 |

Кислов А.Н. |
Атомная физика |
Величина α , называемая поляризуемостью молекулы, характеризует способность электронной оболочки молекулы смещаться относительно положения равновесия при взаимодействии со световой волной. При колебаниях атомов молекулы ее электронная оболочка деформируется. А поскольку деформируемая и недеформируемая электронные оболочки неодинаково смещаются под действием световой волны, то поляризуемость α является функцией межатомного расстояния r: α = α(r) .
Рассмотрим двухатомную молекулу. Разложим ее поляризуемость α(r)
в ряд Тейлора около точки равновесного положения атомов rо по степеням смещений u = r – rо, которые в гармоническом приближении изменяются по закону u = uo cos 2πνколt , и ограничимся первыми двумя членами:
α(r) ≈ α(r )+ |
dα |
|
|
|
u = α(r ) + |
dα |
|
u |
o |
cos 2πν |
кол |
t . |
|
|
|
|
|
||||||||||
|
|
||||||||||||
o |
dr |
|
r |
o |
dr |
|
r |
|
|
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
o |
|
|
|
o |
|
|
|
|
|
=∆α
Следовательно, поляризуемость α(r) молекулы представляется в виде суммы постоянной части α(ro ) и части ∆α, периодически изменяющейся во времени t с частотой νкол вследствие деформации электронной оболочки при ко-
лебаниях атомов.
Таким образом, в гармоническом приближении индуцируемый на моле-
куле электрический дипольный момент d можно записать следующим образом:
d (r) = (α(ro ) + ∆α)Eo cos 2πνоt = d pp + dkp ,
где d pp = α(ro )Eo cos 2πνоt характеризует релеевское когерентное рассеяние с частотой падающего света νo ;
dkp |
= |
dα |
|
|
|
Eouo |
cos 2π(νо − νкол )t + |
dα |
|
|
|
Eouo |
cos 2π(νо + νкол )t |
|
|
||||||||||||
dr |
|
r |
2 |
dr |
|
r |
2 |
||||||
|
|
|
νс |
|
νaс |
||||||||
|
|
|
|
|
o |
|
|
|
|
o |
|
||
обусловливает возникновение некогерентного комбинационного рассеяния света с частотами νc = νo − νкол и νac = νo + νкол.
Интенсивность Ip спутников на частотах νc и νac пропорциональна
квадрату первой производной поляризуемости молекулы по межатомному расстоянию r:
I p ~ ddrα 2 .
ГОУ ВПО УГТУ-УПИ − 2005 |
Стр. 130 из 142 |
