Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

РешОлимпиады 15.05.11

.pdf

Скачиваний:

Добавлен:

23.02.2015

Размер:

479.5 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

1. (Гредасова Н.В.) В некоторой области погода через длительные периоды времени становится то дождливой, то сухой. Если идёт дождь, то с вероятностью 0,(68) он будет идти и на следующий день. Если же в какой-то день стоит сухая погода, то с вероятностью 0,(76) она сохранится и на следующий день. Известно, что в среду погода была дождливая. Какова вероятность того, что она будет дождливой и в ближайшую пятницу?

Р е ш е н и е. Введём обозначения событий:

Dпят Дождьв пятницу , Dчетв Дождьвчетверг , Dср Дождьв среду , Счетв Солнцев четверг , Сср Солнцев среду .

Тогда для искомой условной вероятности имеем

P Dпят / Dср P Dпят / Dчетв P Dчетв / Dср P Dпят /Счерв P Счетв / Dср .

Так как P Dпят / Dчетв P Dчетв /Dср 0,(68)									68		,	а
Так как P Dпят / Dчетв P Dчетв /Dср 0,(68)											,	а
		76	23					99								68		31
P Dпят	/Счерв 1 0,(76) 1	76	23	, P Счетв / Dср 1 0,(68) 1												68		31	, то
P Dпят	/Счерв 1 0,(76) 1		99	, P Счетв / Dср 1 0,(68) 1															, то
	99		99										99				99
	P Dпят		/Dср		68		68			23		31		5337	.
	P Dпят		/Dср									99			.
			99			99		99				99	9801

О т в е т. 5337 .

9801

			xn yn	x y n
2. (Полищук Е.Г.) Доказать неравенство						, если
2. (Полищук Е.Г.) Доказать неравенство			2		2	, если
		y 0.	2		2
n 1,	x 0,	y 0.

Р е ш е н и е. Заметим, что при n 1 неравенство выполнено (как равенство). Далее считаем, что n 1. В силу однородности достаточно доказать, что если

x y 2 , то

xn yn

1. Найдём минимум функции u

xn yn

при условии

x y 2 .

Функция Лагранжа имеет вид

L x, y,

xn yn

2 x y . Из системы

n 1

nyn 1

x y 2

получаем x y 1.

n n 1

Второй дифференциал

d2L

xn 2dx2 yn 2dy2 в точке

x y 1

n n 1

равенd2L

dx2 dy2

т.е.

umin

1n 1n

1 и при

n 1,

x 0,

y 0

неравенство справедливо, если x y 2 . Значит, оно справедливо и без этого условия.

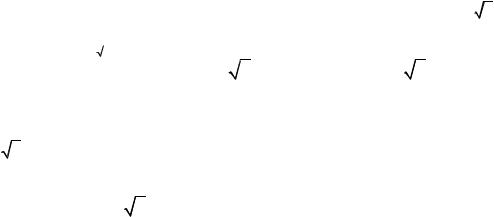
8. (Мохрачева Л.П.) Числовой ряд an сходится. Можно ли утверждать, что

n 1

ряд 1 ean также сходится? Ответ обосновать.

n 1

Р е ш е н и е. Рассмотрим в качестве примера сходящийся ряд

. Тогда

n 1

1 n

1 ean 1 e

1 1

n 1

2! n

n 1

2! n

где

. Таким образом

e n 1,

n , и ряд

расходится. Отсюда

2!n

n 1

1 n

e n

следует, что и ряд

также расходится.

n 1

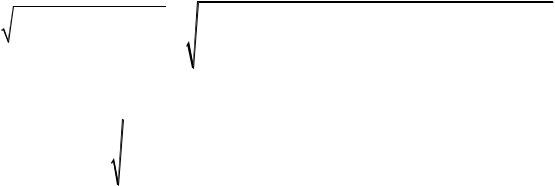
3. (Михалёва М.М.) Найти точку, в которой скорость изменения скалярного поля u arctg x a arctg y b arctg z c

по направлению градиента этого поля будет наибольшей.

Р е ш е н и е. По условию задачи необходимо найти точку глобального мак-

симума функции V x,y,z			u		gradu				, которая определяет скорость
			u
			gradu
			gradu										gradu и его
изменения скалярного поля по направлению градиента. Находим													gradu и его
длину:
				1				1				1
				1				1				1
						2	,			2 ,			2 .
gradu ux	,uy	,uz				2	,			2 ,			2 .
			1 x a				1 y b				1 z c

gradu

ux 2 uy 2

uz 2

1 x a 2 2

1 y b 2 2

1 z c 2 2 .

Таким образом,

V x,y,z

1 x a 2 2

1 y b 2 2

1 z c 2 2

Функция принимает наибольшее значение при

x a,

y b,

z c, так как в

этой точке знаменатели подкоренных дробей равны минимальным значениям, равным 1.

О т в е т. Искомая точка a,b,c .

						1	5			4
4. (Ходак Г.Л.) Вычислить интеграл							x x					dx.
4. (Ходак Г.Л.) Вычислить интеграл							10					dx.
Р е ш е н и е.						1	x	1
Р е ш е н и е.													1
													1		x	5
В силу нечётности подынтегральной функции													1		x		dx 0. Интеграл
В силу нечётности подынтегральной функции													1		x10	1	dx 0. Интеграл
1	x	4		1	1	dx	5		1					1
1		4			1		5
			dx								arctgx5							.
	10		dx			10					arctgx5			1				.
1 x		1	5		1 x	1 5								1		10
1 x		1	5		1 x	1 5										10

О т в е т. .

5. (Андреева И.Ю.) В стране 101 город, соединённые дорогами так, что любые два города соединяет ровно один путь. Сколько в стране дорог?

Р е ш е н и е. Из условия задачи следует, что граф дорог данной страны – дерево. У этого дерева есть висячая вершина. Удалим её вместе с ребром, которое из него выходит. Оставшийся граф также является деревом. Поэтому у него есть висячая вершина, которую мы также удалим вместе с выходящим из неё ребром. Проводя эту операцию 100 раз, мы получим граф, состоящий из одной вершины ( в котором конечно, нет рёбер). Поскольку каждый раз удалялось только одно ребро, то сначала их было 100.

6. (Веретенников Б.М.) Найти матрицы S порядка 2 удовлетворяющие равенству

S 1	4		1		2		1
		4	0	S		0	2	.

Р е ш е н и е.

Пусть	x	y	. Перепишем уравнение в виде
Пусть	S		. Перепишем уравнение в виде
	z	t

4		1 x
	4	0
			z

или

y	x

t	z

y 2		1
	0	2	,
t

4x z 2x

4y t x 2y

4x 2z

4y z 2t

Из первого и третьего уравнений следует

z 2x. Подставляя в четвёртое

уравнение, имеем

2y x t 0

4y 2x 2t 0

т.е. z 2y x. Тогда матрица S имеет вид

2y x

Так как S невырожденная матрица, то

2xy x2 2xy 0. Таким образом,

x,y R,

x 0.

2y x

О т в е т.

x,y R,

x 0.

2y x

7. (Ходак Г.Л.)					f x sin4 tgx cos2 tgx .
Найти экстремальные значения функции					f x sin4 tgx cos2 tgx .
Р е ш е н и е. Переменная t cos2 tgx					принимает все значения из отрезка
0,1 . Тогда	f x y t 1 t 2 t t2 t 1, y 0 y 1 1. График
						1		3
функции y y t - парабола с вершиной в точке							,		.
функции y y t - парабола с вершиной в точке						2	,	4	.
						2		4
О т в е т.	fmin	3	,	fmax 1.
О т в е т.	fmin		,	fmax 1.
	4

			2
9. (Ходак Г.Л.) Решить уравнение y yx y				x yy 0.

Р е ш е н и е. Преобразуем уравнение

yyx 0.

Отсюда следует

yyx C1

или

12 y2 C1 ln x .

Окончательно получаем

1 y2 C1 ln x C2 .

О т в е т.	1	y2 C ln	x	C .
	1

	2	1		2
	2

10. (Веретенников Б.М.) Известно, что следующие параметрические уравнения

x	cost 2	,	y	sint	,

	5 4cost			5 4cost

задают окружность. Найдите центр и радиус этой окружности.

Р е ш е н и е. Пусть					x t					cost 2						. Так как
Р е ш е н и е. Пусть					x t											. Так как
										5 4cost
		cost 2						sint 5 4cost 4sint cost 2																					3sint
x t		cost 2						sint 5 4cost 4sint cost 2																					3sint		,

																5 4cost									2				5 4cost	2
		5 4cost														5 4cost													5 4cost
то точки	t k			есть точки экстремума этой функции. Вычислим значения
функции в этих точках													3			1										1
								x 0					3			1			,		x					1	1.
								x 0											,		x						1.
												9			3										1
Отсюда следует				x	1,				x			1		.
Отсюда следует				x	1,				x					.
				max						min		3						1									1
Аналогично определяем, что											y							1		,	y						1	. Таким образом, уравнение
Аналогично определяем, что											y	max								,	y		min					. Таким образом, уравнение
окружности имеет вид:												max			3								min		3
окружности имеет вид:															2 2
															2 2							2		1
											x						y								.
											x						y							9	.
															3									9
			2	2		2	1
О т в е т.	x			y					.
О т в е т.	x		3	y			9		.
			3				9

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.02.20153.92 Mб15решение.doc
#
22.02.2015226.3 Кб50Решение_MB_15770 (1).doc
#
23.02.2015160.53 Кб10Решения задач ТВ.pdf
#
12.09.201973.22 Кб18Решения задач.doc
#
23.02.2015468.74 Кб14Решения ОЛ.08.04.12.pdf
#
23.02.2015479.5 Кб6РешОлимпиады 15.05.11.pdf
#
23.02.20153.46 Mб21Реьбовые соединения.pdf
#
29.03.201534.91 Кб11РИ - 230501 ТВП весна 2015.docx
#
23.09.2019146.43 Кб3РИ18-программа.doc
#
22.02.2015241.15 Кб4рим.doc
#
08.08.201967.58 Кб2РиМ.doc