
03_05_Сл_вел_Часть_2_2005
.pdf
Лекции 3 – 5 СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
В лекциях рассматривается одно из важнейших понятий теории вероятностей – случайные величины. Рассмотрены различные виды случайных величин, способы их описания, различные числовые характеристики, функции от случайной величины. Обсуждаются наиболее часто встречающиеся законы распределения случайных величин и наиболее часто встречающиеся их функции.
3.1.Случайные величины. Виды случайных величин. Закон распределения случайной величины
3.1.1.Биномиальное распределение. Распределение Пуассона. Поток событий
3.2.Функция распределения случайной величины
3.3.Непрерывная случайная величина. Плотность распределения
3.4.Числовые характеристики случайных величин
3.4.1.Математическое ожидание
3.4.2.Дисперсия. Среднее квадратическое отклонение
3.4.3.Мода, медиана, квантили
3.4.4.Моменты случайных величин
4.1.Основные законы распределения непрерывных случайных величин и их числовые характеристики
4.1.1.Биномиальное распределение
4.1.2.Распределение Пуассона
4.1.3.Равномерное распределение
4.1.4.Показательное распределение
4.1.5.Нормальное распределение (распределение Гаусса)
5.1.Функции от случайной величины
5.2.Числовые характеристики функции случайной величины
5.3.Распределения, связанные с нормальным
5.3.1.Распределение χ2 (Пирсона)
5.3.2.t – распределение Стьюдента
5.3.3.F – распределение Фишера – Снедекора
3.1.Случайные величины. Виды случайных величин. Закон распределения случайной величины
Под случайной величиной понимается величина, которая в результате опыта со случайным исходом принимает то или иное значение.
Возможные значения случайных величин образуют множество Ξ (кси), которое называется множеством возможных значений случайных величин.

28 |
Лекции 3-5 |
Пример:
1.Опыт – бросание игральной кости; случайная величина Х – число выпавших очков. Множество возможных значений Ξ={1,2,3,4,5,6}.
2.Опыт – работа электрического устройства после ремонта; случайная величина Т – время работы устройства до первого сбоя. Множество возмож-
ных значений Ξ: вся правая половина оси Оt (т.е. t≥0). На практике этот участок ограничен справа, но эта граница не определена. Ξ в этом случае несчетно.
Опыт – ведется тестирование изделий до появления первого исправного изделия. Случайная величина Х – число тестов, которое было проведено. Ξ={1,2,3,…,n,…} – бесконечно, но счетно.
ОЕсли множество Ξ конечно (пр.1) или счетно (пр.3), случайная величина называется дискретной, если несчетно (пр.2) – непрерывной.
Таким образом, случайная величина Х – функция элементарного события: Х=ϕ (ω), где ω Ω. При этом множество Ξ возможных значений случайной величины Х состоит из всех значений, которые принимает функция ϕ (ω).
ОЗаконом распределения случайной величины называют любое правило (таблица, функция), позволяющее находить вероятности всевозможных событий, связанных со случайной величиной (например, вероятность того, что случайная величина примет какое-то значение или попадет на ка- кой-то интервал).
Возможны различные способы задания закона распределения. Рассмотрим наиболее типичные.
1. Закон распределения дискретной случайной величины может быть задан в виде таблицы, первая строка которой содержит возможные зна-
чения случайной величины Х: х1, х2, …, хn, …, а вторая – вероятность этих значений Р1, Р2, …, Рn,…, где Рi=P{Х=хi} – вероятность того, что в результате опыта случайная величина Х примет значение хi (i=1, 2, …,
n,…). События х1, х2, …, хn, …, несовместны и образуют полную группу,
n
т.о. ∑Pi =1. Такой закон распределения называется рядом распределе-
i=1
ния.
Пример:
Имеется 3 независимо работающих прибора.
Вероятность нормальной работы 1-го равна 0,2, 2-го – 0,4, 3-го – 0,5. Случайная величина Х – число работающих приборов.
Построить ряд распределения случайной величины Х. Решение:
Возможные значения случайной величины Х: 0,1,2,3. Обозначим работающий прибор «+», а неработающий – «–». Соответствующие вероятности:
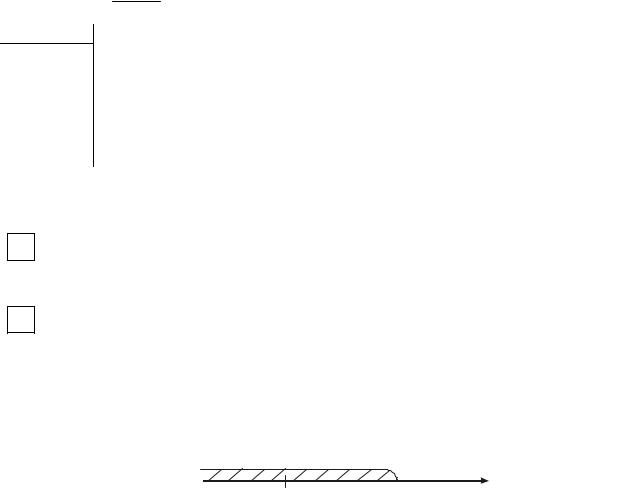
P1 = P(X = 0)={−−−} = 0,8 0, 6 0,5 = 0, 24,
Случайные величины |
29 |
|
P2 = P (X =1)={+−−}+{−+−}+{−−+} = |
= 0, 2 0, 6 0, 5 +0,8 0, 4 0, 5 +0,8 0, 6 0, 5 = 0, 46, |
|
P3 |
= P (X = 2)={+ + −}+{−+ +}+{+ −+}= 0,26, |
|
4 |
|
P4 = P (X = 3)={+++} = 0,04. ∑Pi =1. |
|
i=1 |
X |
0 |
1 |
2 |
P |
0,24 |
0,46 |
0,26 |
2. Закон распределения дискретной случайной величины можно задать графически. Это распределение называется многоугольником распределения. В прямоугольной системе координат строят точки M1 (x1 ;P1 ), M2 (x2 ;P2 ),…, Mn (xn ;Pn ), где хi – возможные значения слу-
чайной величины Х, Рi – соответствующие вероятности, и их соединяют отрезками прямых.
3. Закон распределения, пригодный для всех случайных величин (и дискретных, и непрерывных), может быть задан аналитически: для дискретных случайных величин P(X = xi )=ϕ(xi ).
3
0,04
Pi 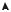
0 |
1 |
2 |
3 xi |
3.1.1.Биноминальное распределение. Распределение Пуассона. Поток событий
Впредыдущей лекции рассматривалась схема повторных испытаний (схема Бернулли) и была получена формула Бернулли, определяющая вероятность появления m успехов в серии из n независимых опытов, в каждом из которых событие А появляется с вероятностью p. Если число успехов рассматривать как случайную величину Х, то очевидно, что она может принимать значения 1,2,3,...,n , а соответствующие вероятности даются полученной
ранее формулой Бернулли:
P ( X = m) =Cm pm qn−m , где q =1− p , C m = |
n! |
. |
|||
m!(n − m)! |
|||||
n |
n |
n |
|
||
|
|
|
|
||
Данное закон распределения называется биноминальным. |
|
||||
В пределе при n→∞, р→0, |
lim(np) = a =const биноминальное распреде- |
||||
|
|
n→∞ |
|
|
|
ление переходит в распределение Пуассона. Случайная величина, распределенная по закону Пуассона, принимает значения 1,2,3,...,n,... с вероятностями
P |
n |
(m)≈ ame−λ . |
|
m! |
|
|
|
Распределение Пуассона можно приближенно применять вместо биномиального, когда число опытов n очень велико, а вероятность p очень мала, т.е. в каждом единичном опыте событие А появляется крайне редко. Приме-
30 |
Лекции 3-5 |
ром применения распределения Пуассона может быть задача, в которой речь идет о многократном применении технического устройства высокой надежности, такой, что вероятность отказа при одном применении очень мала.
Задача: На оси времени Оt случайным образом возникают точки – моменты появления каких-то событий (например, вызовы на телефонной станции, приходы посетителей в магазины и т.п.). Последовательности таких моментов называются «потоком событий». Поток обладает следующими свойствами:
1.Стационарность. Вероятность появления m событий на участке времени τ зависит только от длины τ. Среднее число событий в единицу времени λ=const. называется интенсивностью потока.
2.Ординарность. Вероятность попадания на малый участок ∆t двух или более событий (∆t→0) пренебрежимо мала по сравнению с вероятностью попадания на него 1-го события.
3.Отсутствие последействия. Вероятность появления m событий на любом промежутке времени оси Оt не зависит от того, появились или нет события в предыдущие моменты времени.
Поток, обладающий этими тремя свойствами, называется стационарным. Для
него: P(m)
Пример:
=(λτm!)m e−λτ
Скатода вылетает в среднем q электронов за единицу времени. Какова вероятность того, что за время t вылетит k электронов ?
Решение: а →q , τ →t , m →k. Поток событий является стационарным. Для него
P (k )= (qtk !)k e−qt .
3.2. Функция распределения случайной величины
ООбщей формой закона распределения, пригодной для всех случайных величин (и дискретных и непрерывных), является функция распреде-
ления.
ОФункцией распределения случайной величины Х называется вероятность того, что случайная величина примет значение меньшее, чем заданное х.
Геометрическая интерпретация:
Вероятность того, что случайная точка Х попадает левее заданной точки
х.
X<x
0 |
x |
x |

Случайные величины |
31 |
Основные свойства функции распределения:
1.F (x2 )≥ F (x1 ) при x2 > x1 ;
2.F (−∞)= 0 ;
3.F (+∞)=1.
Покажем геометрически свойство 1: Событие C ={X < x2 }, C = A + B ,
где |
A ={X < x1}, B ={x1 < X < x2 }. |
|
|
||
|
P (C )= P (A)+ P (B), P (X < x2 )= P (X < x1 )+ P (x1 < X < x2 ); |
||||
|
F (x2 )= F (x1 )+ P (x1 < X < x2 ), |
|
|
||
и так как |
P (x1 < X < x2 )≥ 0, |
|
|
|
|
то |
F (x2 )≥ F (x1 ). |
|
|
|
|
|
|
A |
B |
|
|
|
|
|
|
|
|
|
0 |
x |
x2 |
||
|
1 |
|
|
||
C
Таким образом, функция распределения является неубывающей функцией и ее значения заключены между 0 и 1.
Из равенств следует, что вероятность того, что случайная величина Х в результате опыта попадает на участок от х1 до х2 (включая х1) равна приращению функции распределения на этом участке, т.е. P{х1≤Х<х2}=F(х2) - F(х1). Пусть точка х2 неограниченно приближается к точке х1. В пределе имеем
P( X = x1) = lim (F(x2 ) − F(x1)).
x2 →x1
Таким образом, вероятность того, что случайная величина Х примет значение х1, равна скачку ее функции распределения в точке х1 (если функция F(x) разрывна). Если же функция распределения непрерывна в точке х1, то эта вероятность равна О. Если функция F(х) везде непрерывна, то вероятность каждого отдельного значения случайной величины Х равна 0.
Функция распределения дискретной случайной величины
Зная ряд распределения дискретной случайной величины, построим ее функцию распределения. Рассмотрим приведенный ранее ряд распределения случайной величины Х:
X |
0 |
1 |
2 |
3 |
P |
0,24 |
0,46 |
0,26 |
0,04 |
1.х≤0, т.к. число приборов отрицательным быть не может,
то для х≤0 F(х)=0;
2.0<х≤1 F(x)=P{X=0}=0,24;
32 |
Лекции 3-5 |
3.1<x≤2 F(x)=P{X<x}= P{X=0}+P{X=1}=0,24+0,46=0,70;
4. 2<x≤3 F(x)=P{X=0}+P{X=1}+P{X=2}=0,24+0,46+0,26=0,96;
5.х>3 F(x)=P{X=0}+P{X=1}+P{X=2}+P{X=3}=1.
Представим ряд распределения и функцию распределения F(x) графически
3.3.Непрерывная случайная величина. Плотность распределения
Случайная величина Х называется непрерывной, если ее функция распределения является непрерывной и дифференцируемой в любой точке. В качестве закона распределения, имеющего смысл только для непрерывных случайных величин, введем понятие плотности распределения или плотности вероятности. Пусть ∆х - бесконечно малый интервал на оси Ох. Вероятность того, что случайная величина Х примет значение, заключенное между х и х+∆х, равна Р{x≤X<х+∆х}. Разделим ее на ∆х, получим плотность вероятно-
сти |
P{x ≤ X < +∆x} |
, но вероятность попадания случайной величины Х на |
||||
∆x |
||||||
|
|
|
|
|
||
участок равна приращению |
функции распределения на этом участке |
|||||
F( x + ∆x ) − F( x ) , переходя к пределу при ∆х→0, получим |
||||||
|
∆x |
|
F(x + ∆x) − F(x) |
|
||
|
|
|
′ |
|||
|
|
lim |
|
|
= F (x) . |
|
|
|
|
∆x |
|||
|
|
∆x→0 |
|
|
||
Таким образом, плотностью распределения (или плотностью вероятности) непрерывной случайной величины Х в точке х называется производная ее функции распределения в этой точке.
Обозначение: f ( x ) = F′( x ) = dxd F( x ). График плотности распределения ƒ(x)
называется кривой распределения.

Случайные величины |
33 |
Рассмотрим элементарный участок dx. Вероятность попадания случайной величины Х на этот участок dx (с точностью до бесконечно малых высших порядков) равна ƒ(x)dx=dF(x).
Величина ƒ(х)dx называется элементом вероятности для точки. Геометрически - это площадь заштрихованной области. Рассмотрим вероятность попадания случайной величины Х на участок от α до β. Эта вероятность равна сумме элементов вероятности на этом участке, т.е. определенному
β
интегралу: P{α < X < β} = ∫ f (x)dx .
α
На рисунке заштрихованная область.
|
F( x ) = P{ X < x } = P{ −∞ < X < x } = ∫x |
f ( x )dx . |
|
−∞ |
|
Свойства плотности распределения: |
|
|
1. |
ƒ(x)≥0; |
|
2. |
∞∫ f ( x )dx =1. |
|
|
−∞ |
|
Пример:
Функция распределения непрерывной случайной величины Х задана выражением
0, при x ≤ 0, F(x)= x2 , при 0<x ≤1,
1, при 1<x
Найти:
1.Плотность распределения ƒ(х) случайной величины Х и построить ее граграфик;
2.Найти вероятность того, что случайная ве-
личина Х в результате опыта примет значение между 0,25 и 0,5.
1) |
|
0, при x ≤ 0, |
f (x) = F '(x) = |
|
|
|
2x, при 0 < x <1, |
|
|
|
|
|
|
0, при x >1 |
или ƒ(x)= 2x при 0<x<1.
2) Вероятность попадания случайной величины
Х на участок (0,25;0,5): P{ 0,25 < X < 0,5 } = 0∫,5 f ( x )dx , но можно воспользо-
0,25
ваться формулой: P{0,25<X<0,5}= F(0,5)-F(0,25)=0,52-0,252=0,1875.
34 |
Лекции 3-5 |
3.4.Числовые характеристики случайных величин
Втеории вероятностей числовые характеристики играют огромную роль. С их помощью существенно облегчается решение многих задач. Среди числовых характеристик случайной величины рассмотрим сначала характеристику положения, фиксирующую положение случайной величины на числовой оси, т.е. некоторое среднее, ориентировочное значение случайной величины, около которого группируются ее возможные значения. Такой характеристикой является математическое ожидание, иногда ее называют средним значением случайной величины.
3.4.1. Математическое ожидание
ОМатематическим ожиданием дискретной случайной величины называется сумма произведений всех возможных ее значений на вероятности
этих значений.
M(X )= ∑xi pi = mx
i=1n
Пример:
Дано распределение случайной величины. Найти М(Х).
|
X |
2 |
3 |
4 |
5 |
|
M (X |
P |
0,1 |
0,2 |
0,2 |
0,5 |
|
)= m(x)= |
2 0,1 + |
3 0,2 + 4 0,2 +5 0,5 = 4,1. |
||||
!При достаточно большом числе опытов можно среднее арифметическое наблюденных значений случайной величины принимать приближенно равным ее математическому ожиданию.
Свойства математического ожидания:
1.М(с)=с, с- константа;
2.М(сХ)=сМ(Х).
ОМатематическим ожиданием непрерывной случайной величины Х с
плотностью ƒ(х) называется величина mx = M (X )= ∞∫ x f (x)dx .
−∞
Пример:
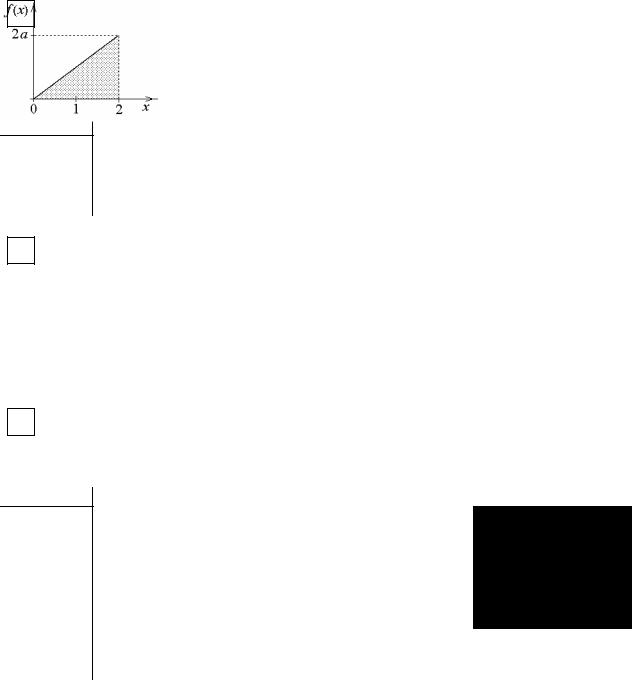
Непрерывная случайная величина Х распределена на участке (0,2) с плотностью распределения ƒ(x)=ax при x (0,2). Найти коэффициент а и математическое ожидание mx
Решение:
Построим график ƒ(x).
коэффициент а найдем из условия, что S∆=1. S∆ = 12 2 2a =1. Следовательно, a = 12 .

Случайные величины |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
35 |
|
|
mx = |
2 |
x |
1 |
x dx = |
1 |
2 |
x2dx = |
1 x3 |
|
2 |
= |
8 |
= |
4 |
≈1,33 . |
||
|
|
|||||||||||||||||
|
|
|||||||||||||||||
∫ |
|
|
∫ |
|
|
|
|
|
|
|
||||||||
2 |
2 |
2 3 |
|
|
|
6 |
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3.4.2. Дисперсия. Среднее квадратическое отклонение
Характеристикой отклонений случайной величины от ее математического ожидания является дисперсия, описывающая рассеяние случайной величины относительно среднего значения.
ОДисперсией случайной величины Х D(x)=Dx называется Dx=M((X-Mx)2), где разность X-Mx называется отклонением случайной величины Х от ее математического ожидания.
Для непосредственного вычисления дисперсии служат формулы:
n
Dx = ∑( xi −mx )2 pi – для дискретной случайной величины,
i=1
Dx = ∞∫(x − mx )2 f ( x )dx – для непрерывной случайной величины.
−∞
На практике пользуются формулой: Dx=M(X2)-(M(X))2, т.е. дисперсия случайной величины равна математическому ожиданию ее квадрата минус квадрат математического ожидания. Она получается из определения:
Dx = M ((X −Mx )2 )= M (X 2 −2X Mx + Mx2 )=
=M (X 2 )− 2M (X M x )+ M (M x2 )=
=M (X 2 )−2M x M x + M x2 = M (X 2 )− M x2 .
Свойства дисперсии:
1.Dx≥0;
2.Dс=0;
3.D(cx)=c2Dx;
4.D(X+Y)=DX+DY (X,Y-независимые случайные величины);
5.D(C+X)=DX.
Пример:
В техническом устройстве работают независимо 2 блока. Вероятность безотказной работы первого блока p1=0,4, второго – p2=0,7. Случайная величина Х
– число работающих блоков. Найти ее математическое ожидание и дисперсию.
Решение: Случайная величина Х принимает значения 0, 1, 2. Вероятности этих значений: P{X=0}=0,6·0,3=0,18; P{X=1}=1-(0,18+0,28)=0,54; P{X=2}=0,4·0,7=0,28.
Ряд распределения случайной величины Х:
X |
0 |
1 |
2 |
P |
0,18 |
0,54 |
0,28 |
mx=0·0,18+1·0,54+2·0,28=1,1.
Дисперсия Dx=M(X2)-(M(X))2,

36 |
Лекции 3-5 |
(M(X))2=(1,1)2=1,21,
Найдем M(X2)=02·0,18+12·0,54+22·0,28=1,66. Dx=1,66-1,21=0,45.
Дисперсия имеет размерность квадрата случайной величины. Для наглядности в качестве характеристики рассеивания удобнее пользоваться числом, размерность которого совпадает с размерностью случайной величины.
Величина Dx =σx называется средним квадратическим отклонением
случайной величины (с.к.о.).
Для сравнения различных случайных величин бывает удобно привести их к стандартному виду: начало отсчета перенести в точку, совпадающую с математическим ожиданием с.в., а масштаб выбрать так, чтобы в новых единицах с.к.о. было равно единице.
О Случайная величина Y = |
X − MX |
называется стандартной случайной |
|||||||||
σx |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
величиной, соответствующей случайной величине X . |
|
|
|
||||||||
|
X − MX |
|
MX − MX = 0 , |
|
X − MX |
|
DX |
|
|
||
MY = M |
= |
DY = D |
= |
|
=1. |
||||||
σx |
σx |
(σx ) |
2 |
||||||||
|
|
σx |
|
|
|
|
|||||
3.4.3. Мода, медиана, квантили
Кроме математического ожидания в качестве характеристики положения применяют моду и медиану случайной величины.
ОМода дискретной случайной величины – это наиболее вероятное значение случайной величины; для непрерывной случайной величины – это точка максимума плотности распределения. Обозначение: Мoх.
Пример:
 На рисунке представлен многоугольник распределения. Для данной дискретной случайной величины Х мода Мoх =2.
На рисунке представлен многоугольник распределения. Для данной дискретной случайной величины Х мода Мoх =2.
Для непрерывной случайной величины на рисунке представлена кривая распределения случайной величены. Мoх – точка, в которой плотность распределения ƒ(х) имеет максимум.
Мода может быть не единственной. Такое распределение называется полимодальным. В этом случае часто статистический материал, использованный в исследованиях, является разнородным.
