
- •Колебания §1.Гармонические колебания и их характеристики
- •§2. Векторная диаграмма
- •§3. Кинематические и динамические характеристики
- •§7.Энергия колебаний в контуре
- •§8.Сложение одинаково направленных гармонических колебаний одинаковой частоты
- •§8.1.Сложение одинаково направленных колебаний с близкими частотами (биение)
- •§9. Сложение взаимно перпендикулярных гармонических колебаний с кратными частотами. Фигуры Лиссажу
- •§10. Затухающие механические колебания
- •§11. Характеристики затухающих колебаний
- •§12. Затухающие колебания в затухающем контуре
- •§13. Характеристики затухающих электромагнитных колебаний.
- •§14. Вынужденные колебания
- •§15. Резонанс
- •§16. Вынужденные колебания в колебательном контуре
- •§17. Автоколебания
- •Волны в упругих средах
- •§1.Механические волны
- •§2. Характеристики волны
- •§3.Уравнение плоской монохроматической волны
- •§4. Волновое уравнение
- •§5. Стоячие волны
- •– Узлы.
- •Выводы:
- •На стоячей волне укладывается целое число полуволн;
- •§6. Характеристики звуковых волны
- •§7. Эффект Доплера
- •§8. Ультразвук и его применение
- •§9. Свойства механических волн
- •§10. Электромагнитные волны
- •§11. Излучение и прием электромагнитных волн
- •Оптика §1. Развитие взглядов на природу света
- •§2. Законы геометрической оптики
- •§3. Волновая оптика §4. Интерференция света
- •§5. Способы получения когерентных источников света
- •§6.Расчет интерференционной картины от двух когерентных источников света (опыт Юнга)
- •§7. Оптическая длина пути и оптическая разность хода интерференции световых волн
- •§9.Кольца Ньютона
- •§10.Применение интерференции света
- •§11.Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля. Зонная пластинка
- •§12.Дифракция Френеля на диске
- •§13.Дифракция Френеля на круговом отверстии
- •§14.Дифракция в параллельных лучах на одной щели
- •§15.Дифракция на дифракционной решетке
- •§16.Характеристики дифракционной решетки
- •§17.Дифракция на пространственной решетке
- •§18.Поляризация света
- •§19.Анализ поляризованного света. Закон Малюса
- •§20. Поляризация света при отражении. Закон Брюстера
- •§21. Двойное лучепреломление. Поляроиды и поляризационные призмы
- •§22. Тепловое излучение
- •§23. Характеристики теплового излучения
- •§24. Закон теплового излучения. Закон Кирхгофа
- •§25. Законы излучения ачт
- •Закон Стефана-Больцмана: энергетическая светимость ачт t4,
- •§26. Квантовая гипотеза. Формула Планка
- •§27. Оптическая пирометрия
- •§28. Фотоэлектрический эффект
- •§29. Внешний фотоэффект
- •§30. Законы фотоэффекта
- •§31. Уравнение Эйнштейна для фотоэффекта. Объяснение законов фотоэффекта
- •§32. Фотоны. Давление света
- •§33. Эффект Комптона
- •§34. Корпускулярно-волновая двойственность(дуализм) света
- •§35. Элементы квантовой механики. Двойственная корпускулярно-волновая природа частиц вещества. Идея де Бройля
- •§36.Соотношение неопределенностей Гейзенберга как проявляется волновых свойств
- •§37.Вероятностный смысл волн де Бройля. Волновая функция
- •§38.Свойство волновой функции
- •§39.Уравнение Шредингера
- •§40.Уравнение Шредингера для свободной частицы
- •§41.Частица в одномерной прямоугольной потенциальной яме с бесконечно высокими степенями
- •§42.Энергия частицы в потенциальной яме
- •§43.Прохождение частицы через потенциальный барьер. Туннельный эффект
- •§44.Элементы современной физики атомов и молекул
- •§45Спектр излучения атомов водорода
- •§46Опыты Штерна-Герлаха Спин электрона.
- •§47 Многоэлекторонные атомы. Распределение электронов в атоме по состояниям. Принцип Паули.
- •§48Переодическая система элементов Менделеева
- •§49Элементы квантовой электроники. Спонтанные и вынужденные излучения.
- •§50 Оптические квантовые генераторы (Лазеры)
- •§51 Элементы данной теории твердых тел
- •§52 Собственные и приместные полупроводники
- •§53 Приместные полупроводники
- •Элементы физики атомного ядра
- •§1 Размер, состав и заряд атомного ядра. Массовое зарядовое число.
- •§2 Деффект массы и энергия связи ядра
- •§3 Ядерные силы и модели ядра
- •§4 Радиактивное излучение и его виды
- •Виды радиоактивного излучения
- •§5 Закон радиоактивного распада. Правило смещения.
- •§6 Ядерная реакция
§12. Затухающие колебания в затухающем контуре
В колебательном контуре имеется C, L, R.

При протекании тока через сопротивление на нем выделяется тепло, которое можно рассчитать по закону Джоуля-Ленца.
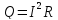
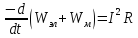
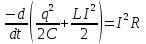




Решением дифференциального уравнения является выражение:



Вследствие этого свободная энергия с течением времени уменьшается, по закону сохранения энергии.
§13. Характеристики затухающих электромагнитных колебаний.
Коэффициент затухания
 .
.Частота затухающих колебаний
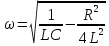
Период затухающих колебаний

Декремент затухания – это отношение двух соседних амплитуд
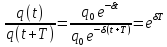
Логарифмический декремент затухания (λ)

Время релаксации
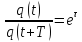 ;
;
Число колебаний(N) – это количество колебаний, которое совершает система за время релаксации
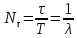
Добротность системы


В колебательном контуре, содержащем C, L, R возможны следующие режимы работы:
 .
Будет происходить периодическое
изменение заряда на обкладках
конденсатора, такой режим работы
называется периодическим.
.
Будет происходить периодическое
изменение заряда на обкладках
конденсатора, такой режим работы
называется периодическим. .
Колебания заряда не происходит, частота
таких колебаний называется мнимой,
режим такой работы называется
апериодический
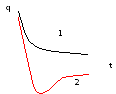
(сильное затухание). Смотри на рисунке
кривая1.
.
Колебания заряда не происходит, частота
таких колебаний называется мнимой,
режим такой работы называется
апериодический
(сильное затухание). Смотри на рисунке
кривая1. .
Режим работы критический.
Смотри на рисунке кривая 2.
.
Режим работы критический.
Смотри на рисунке кривая 2.
 ,
,

§14. Вынужденные колебания
Вынужденные колебания – это колебания, происходящие под действием внешней, периодически изменяющейся силы. В отличие от свободных (собственных колебаний) при вынужденных колебаниях необходимо подкачка энергии.
Частота установившихся вынужденных колебаний должна быть равна частоте изменения внешней силы

Внешняя сила пополняет энергию системы и расходуется на работу против силы сопротивления. С течением времени устанавливаются колебания с постоянной амплитудой. Кроме внешней силы в системе действует сила упругости и сила сопротивления.

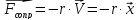








Решением
уравнения (*) ищем в виде

Знак «-» так как трение тормозит колебания, которые отстают по фазе от колебаний вынуждающей силы.

В
данном уравнении неизвестна A,
– фазовый сдвиг, найдем x и
x
и
x .
.


Выпишем все в правой части в уравнение (*) и ее правую часть.
 данные
выражения можно рассматривать как
принцип связанных векторов,
которые
вращаются вокруг точки O
с угловой частотой
данные
выражения можно рассматривать как
принцип связанных векторов,
которые
вращаются вокруг точки O
с угловой частотой
 и имеющих длины
и имеющих длины ,
, ,
, и сдвинутых по фазе по отношению к
вектору
и сдвинутых по фазе по отношению к
вектору на
на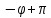 ,
, ,
, .
.
Остановим
вращение этих векторов в момент, когда
 .
.
Тогда



Возможны
два случая: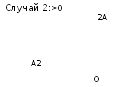

В
обоих случаях сложим векторы x и
и
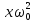 .
.

По
уравнению (*) сумма


Из
рисунка видно, что вектор
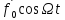 опережает вектор
опережает вектор на угол
на угол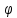 .
Найдем величину фазового сдвига.
.
Найдем величину фазового сдвига.
1:
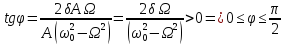
2:

Итак,
 –
угол, определяющий сдвиг по фазе между
установившимися вынужденными колебаниями
и внешней силой.
–
угол, определяющий сдвиг по фазе между
установившимися вынужденными колебаниями
и внешней силой.
Проанализируем данное выражение:
Если

Если

Если

Изобразим на графике:

Найдем амплитуду вынужденных колебаний А.
Для
обоих случаев

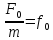

Амплитуда зависит от f0(амплитуда внешней вынуждающей силы) от m,, n, соотношения, n, . Исследуем зависимость А().
=0;
 –амплитуда постоянно в состоянии
статической нагрузки.
–амплитуда постоянно в состоянии
статической нагрузки.
Fвынужд.= F0cost=F0


– закон Гука.
– закон Гука.
, А0, т.е. система не успевает за изменениями.
В системе совершающей вынужденные колебания происходит резонанс.
§15. Резонанс
Резкое возрастание амплитуды вынужденных колебаний по мере их приближения к 0 или 0 к называется резонансом.
Найдем резонансную частоту:







ПриAрез (острее резонансная кривая).
Если =0,Арез=

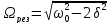
Если
22 ,
то рез=0
или мнимое
резонанса нет.
,
то рез=0
или мнимое
резонанса нет.
При
малом затухании, 0,
 (добротность)
(добротность)
Q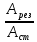
острее резонанс.
острее резонанс.
Полезное использование резонанса:
Радиотехника. Наличие резонанса позволяет обнаружить даже очень слабые колебания, если их частота совпадает с собственной частотой прибора.
Вредное использование резонанса:
Разнос турбин в воздухе, «рота солдат».
Почему происходит резонанс?
Fвынужд=F0cost
x=Acos(t–)
V=x=
–Asin(t–);
=
Тк при резонансе0=,V=–Asin(t–);
V=–A0sin(0t–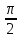 );
=A0cos(0t)=–Acost.
);
=A0cos(0t)=–Acost.
Скорость совпадает по фазе с Fвынужд., идет раскачка колебаний в такт резонанс.
