§40.Уравнение Шредингера для свободной частицы

Свободная частица – это частица, движущая в отсутствии внешних полей. Рассмотрим частицу, которая движется только вдоль оси ox, т.к. она свободная U(x)=0.E_полн.=E_кин.

Обозначимкакk²: . Решением данного уравнения является уравнение., где Aи k некоторые const. Найдем собственные значения энергии частицы:

Вывод: энергия свободной частицы E так же как и волновое число k, может принимать любые значения, т.е. энергетический спектр энергий непрерывный. Таким образом, свободная микрочастица описывается плоской монохроматической волной де Бройля. Вероятность(плотность вероятности) обнаружения частиц данной точке–A²., т.е. все положения частицы в пространстве равновероятны.

§41.Частица в одномерной прямоугольной потенциальной яме с бесконечно высокими степенями

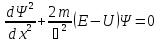(*) – общее стационарное уравнение Шредингера.

Так как яма имеет бесконечно высокие стенки, частица не может проникнуть за пределы ямы, поэтому вероятность обнаружения частицыa волновой fза пределами ямы равна нулю. На границах ямы в точке x=0и x=l волновая f вследствие ее непрерывности так же как должна обращаться в ноль ,.

В пределах ямы (*) имеет вид: (1), где.

Общее решение уравнения (1) имеет вид: ,гдеA, B– const, т.к. , тоB=0выполняется, когда kl=n, где n – целое число, ; .

На длине ямы l должно укладываться целое число длин полуволн, образуя стоячую волну, причем возможность длины волны _n принимают дискретный ряд значений .

Постоянную A найдем из условия нормировки: ,



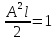
–собственные значения функции, где n – целые числа.

§42.Энергия частицы в потенциальной яме

; ;, гдеn – целые числа.

Вывод: энергия частицы в потенциальной яме не может быть любой. Она принимает лишь ряд дискретных собственных значений. Поэтому говорят, что энергия частицы в потенциальной яме квантована. Квантованные значения энергии называются уравнениями энергии, а n – квантовые числа.

Таким образом, частица в потенциальной яме может находиться на определенном энергетическом уровне или в определенном состоянии n.

E=E_n+1–E_n– интервал между соседними энергетическими уровнями.

l=10^-9мE

, если n>>1, 2n+12n, т.е. соседние уровни энергии частицы в потенциальной яме расположены тем теснее, чем больше n.

§43.Прохождение частицы через потенциальный барьер. Туннельный эффект

§44.Элементы современной физики атомов и молекул

Атом водорода в квантовой механике.

Решение задачи о нахождении ровнейэлектрона в системе сводится к задаче о движении электрона в Кулоновском поле ядра. В случае многоэлектронных атомов рассматривается кулоновское взаимодействие между одним электроном и эффективным ядром. Потенциальная энергия взаимодействия электрона с ядром обладающая зарядом ., «-»-электрон находится внутри потенциальной ямы гиперболической формы.

Состояние электрона описывается уравнением Шрейдингера:

Ядро можно считать точечным зарядом обладающим сферически полем, следовательно уравнению Шрейдингера. Можно рассматривать в сферических координатах, т.е. от координат x,y,z к сферическим (r,θ,φ). Поэтому решение уравнения Шрейдингера зависит от ,-радиальный сомножитель;-угловой сомножитель.

Можно показать что с учетом ограничений накладываемых на волновую функцию (непрерывность, однозначность и конечность) собственные значения энергии зависят от 3-х целочисленных параметров:n,l,m_l

1n-определяет вид радиальной части, определяет энергетические уровни электронов в водородной системе и называется квантовым числом.

- энергия n-го энергетического уровня.

Для Н: z=1; =-3.38эВ;

Энергетический спектр атома водорода дискретный. Е₁-основное состояние атома; Е₂,Е₃…Е_n-возбужденное состояние.

Е<0-движение электрона является связанным, т.к. он находится внутри потенциальной ямы;

E>0-движение электрона является свободным и соответствует ионизированному атому.

Энергия иоинизации атома Н: . В угловой сомножитель волновой функции входятдва параметраlи m_l, l-орбитальное квантовое число, оно определяет модуль момента импульса электрона связанного с орбитальным движением электрона и ядра.

В классической механике ограничения на числовые значения l нет.

Движение электрона подобно круговому току, это значит, что вращающийся электрон обладаетмагнитным моментом. .

Существуют Гиромагнитные соотношения которое связывает:

Если задана n, то l=1,2,…,n-1.

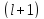-орбитальный момент импульса квантуется

l=0 то электрон нахолдится в S-состоянии;

l=1 то электрон нахолдится в P-состоянии;

l=2 то электрон нахолдится в d-состоянии;

l=3 то электрон нахолдится в f-состоянии;

l=4 то электрон находится в g-состоянии; из решения уравнения Шрейдингера следует,что вектор арбитального импульса электрона может иметь только такие ориентации в пространствепри которых его проекция на направление внешнего магнитног поля приним ает квантовынные значения пропорциональные

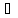
2l+1

P-состояниеl=1,

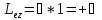
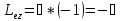
В магнитном поле вектр орбитального момента импульса имеет 2l+1 ориентацию.Наличие магнитного квантированного числа приводит к расщиплению в МП уровня с главным квантовым числом на 2l+1 под уровней. Следовательно что в спектре атома наблюдается расщипление спектральные линии, этот эффект называется эффектом Зеемана.

Хотя энергии электрона зависит от главного квантового числа n, но каждому собственному числу E_n(кроме E₁) соответствует несколько собственных значений функций 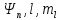отличающихся значениями.

Состояние электрона с одинаковой энергией но с разными квантовыми числами называется вырожденным. Числа nиl характеризуют размер и форму электроного облака, а квадрат волновой функции – определяет вероятность обнаружения электронов в еденице объёма атома. Эта вероятность различна в разных местах атома. Электрон как бы размазан по объему атома образуя электронное облако плотность и густота которого характеризуется вероятностью обнаружения электронов в различных точках объема.

nи lхарактеризует размер и форму облака, -характеризует его ориентацию в пространстве.

1S n=1 l=0 =0

2S n=2 l=0 =0

2P n=2 l=1