§37.Вероятностный смысл волн де Бройля. Волновая функция

Квадрат амплитуды световой волны является мерой вероятности попадания фотонов в какую-либо точку:A^2~W, J^~A². Из опытов о дифракции электронов обнаруживается не одинаковое распределение пучков электронов, отраженных или рассеянных по любым направлениям, т.е. вероятность попадания электронов в любую точку экрана неодинакова. С волновой точки зрения это соответствует любой интенсивности волн де Бройля, т.е. J волн в данной точке пространства позволяет определить число электронов, попавших в эту точку за одну секунду |A²|^~W.

Модуль квадрата A волны де Бройля в данной точке пространства является мерой вероятности того, что частица обнаруживается в этой точке. Чтобы описать распределение вероятности нахождения частицы в данный момент времени в некоторой области пространства вводят волновую функциюΨ(x, y, z, t), которая зависит от координат и времени. Вероятность ΔW, что частица находится в объеме dv пропорциональна Ψ² иdv. dW=|Ψ| ²dv=| Ψ |²dxdydz

| Ψ |²= Ψ۬۬۠ Ψ^*, Ψ^*- где сопряженная.

| Ψ |²-имеет смысл плотности вероятности.

, т.е. определяет вероятность нахождения частицы в данной точке пространства или определяет интенсивность волн де Бройля.

Вероятность ΔW найти частицу в момент времени t в конечном объеме V:

Из определения волновой следует, что она должна удовлетворять условию нормировки. Нормировать Ψ следует так, чтобы вероятность достоверного события обращалась в единицу. Если за объем V принять бесконечный объем всего пространства это означает, что при данном условии частица должна находиться где-то в пространстве:

§38.Свойство волновой функции

Ψ функция должна быть:

1. Конечной, т.к вероятность не может быть больше единицы;

2. Однозначной, т.к. вероятность не может быть многозначной величиной;

3. Непрерывной, т.к. вероятность не может изменяться скачками.

Волновая функция удовлетворяет принципу суперпозиции. Если система находится в любых состояниях вписываемых волновыми f, Ψ₁,Ψ₂, Ψ₃ , то она может находиться в состоянии Ψ, описываемой линейной комбинацией этих функций: .

§39.Уравнение Шредингера

Так как положение частицы в пространстве в квантовой механике задается через волновую функцию Ψ(x, y, z, t)то основное уравнение квантовой механики должны быть уравнением этой функции Ψ.

В 1906г. Уравнение Шредингера постулируется:

(*), где,,m – масса частицы,  – оператор Лапласа, U(x, y, z) – Wp частицы в силовом поле, i– мнимая единица, . (*) – временное (общее) уравнение Шредингера. Оно справедливо для любой частицы массойm, с V<<c.

Решение этого уравнения можно записать в виде: , где– координатная часть волновой функции,– временная часть волновой функции.

При решении ряда физических задач микромира необходимо учесть находить стационарное решение уравнения Шредингера (не содержащее время). Это имеет смысл, когда U=U(x, y, z), т.е. ее амплитудная часть.

Уравнение Шредингера: 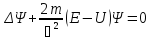, гдеE – полная энергия частицы. Решением данного уравнения будут волновые функции, которые удовлетворяют свойствам функции: однозначность, конечность, непрерывность. Волновыхf, удовлетворяющие уравнению Шредингера при данном значении потенциальной энергии, называется собственными функциями, а значения полной энергии E, при которой существует решение уравнения Шредингера, называется собственными значениями энергии.