Колебания §1.Гармонические колебания и их характеристики
Колебания – это частный случай периодического движения, при котором система через равные промежутки времени (период) возвращается в исходное состояние равновесия.
Виды колебаний:
Свободные или собственные(это колебания, происходящие в системе предоставленной самой себе после выведения ее из состояния равновесия). Для того чтобы колебания были периодическими необходимо сообщать системе энергию.
Затухающие и незатухающие(если есть трение в системе то затухающие, иначе незатухающие).
Вынужденные (колебания, обусловленные внешним периодическим воздействием).
Гармонические (колебания, происходящие по закону синуса или косинуса). Являются простейшим видом колебаний.
§2. Векторная диаграмма
Графически
гармонические колебания можно изобразить
с помощью метода векторных диаграмм.
Пусть вокруг точки О равномерно вращается
некоторый вектор
.
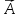ω0 – циклическая (угловая) частота (скалярная величина, характеризующая быстроту изменения фазы колебаний в единицу времени).
Спроецируем
на осьxи
y.
x,y – смещение (может быть как >0, так и <0). Если смещение максимальное, то появляется амплитуда колебаний (А всегда>0).
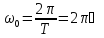
xmax=A, гдеA–амплитуда колебаний.
Т – период колебаний[с](наименьший промежуток времени, в течение которого изменяющаяся физическая величина, повторяющаяся по модулю и направлению). Если через промежуток времени ∆t совершается N колебаний, то
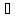–линейная
частота [Гц, 1/с]
§3. Кинематические и динамические характеристики
Дифференциальное уравнение свободных незатухающих колебаний
Рассмотрим
гармоническое колебание
.
Найдем скоростьколебания:
A0=Vmax
Ускорение:
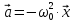
Гармонические
колебания происходят под действием
упругой или квази упругой силы.
– однородное линейное дифференциальное уравнение второго порядка. Дифференциальное уравнение свободных незатухающихгармонических колебаний. Решением этого уравнения является уравнение
.
§4. Пружинный и математический маятник
Математический маятник – это тело, подвешенное на невесомой нерастяжимой нити, размерами и формами которого можно пренебречь.
В
момент времени
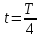
В
момент времени
В
момент времени
В
момент времени
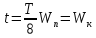
4
раза за период происходит превращение
потенциальной энергии в кинетическую
и наоборот.
Груз на пружине (принцип маятника)
k–
коэффициент упругости;
m – масса груза.
§5. Энергия гармонических колебаний
В
уравнения
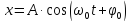и
примем, что начальная фаза
,
то тогда
и
.
В
момент времени
В
момент времени
В
момент времени
Найдем потенциальную энергию.
§6. Свободные незатухающие колебания в колебательном контуре
Незатухающие колебания возникают в колебательном контуре, в котором имеется катушка индуктивности L и конденсатор C, активное сопротивление R=0.
В таком контуре происходит перекачка энергии конденсатора (электрическая энергия) в энергию токов катушки (магнитная, аналог кинетической) и обратно.
В
момент времени
Конденсатор полностью заряжен.
.
В
момент времени
Конденсатор
разряжается и в контуре потечет ток,
поэтому возникает магнитное поле в
катушке индуктивности и к моменту
времени
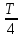
–max
В
момент времени
Ток начинает уменьшаться и по правилу Ленца в катушке будет индуцироваться ток того же направления, что и ток разряда конденсатора. Конденсатор начинает перезаряжаться.
–max
В
момент времени
Выведем дифференциальное уравнение свободных гармонических колебаний в контуре.
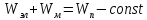
Возьмем производную по времени:
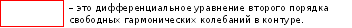
Сравним
с
.
Решением
нашего является
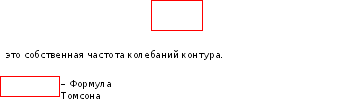
Таким
образом,q,
I
колеблются гармонически с одинаковыми
периодами, но со сдвигом по фазе
.
