38Прямой и наклонный геликоиды. Образование, задание, применение

Прямой геликоид имеет другое название – прямой коноид, т.к. прямолинейные образующие пересекают ось и винтовую направляющую, оставаясь параллельными одной и той же плоскости, перпендикулярной оси геликоида. Поэтому эта поверхность может быть задана двумя способами и иметь два определителя Г (i, l h), и Г (i, a, T), где i – ось геликоида, l – образующая прямая, h – шаг винтового движения, а – направляющая, T – плоскость параллелизма, которая может совпадать с П1 либо с П2

 Для получения наглядного изображения поверхности ее задание проекциями геометрической части определителя следует расширить до задания каркасом, состоящим из последовательных положений прямолинейных образующих винтовых линий.

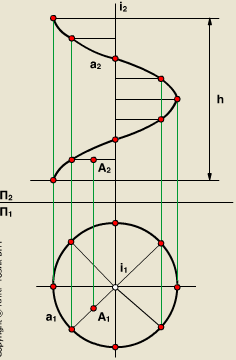
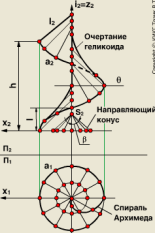
 Наклонный, или архимедов, геликоид отличается от прямого геликоида тем, что его прямолинейная образующая пересекает ось i геликоида под постоянным углом . Образующая геликоида пересекая две направляющие ось i и направляющую гелису а на цилиндре, остается параллельной образующим некоторого конуса вращения с вершиной S имеющего общую ось с винтовой линией и угол между образующей и осью, равный углу .

35Образование поверхностей. Способы их задания

Существует два основных способа образования поверхностей – движением

линий или поверхности.

Рассмотрим первый способ, необходимый для выполнения третьей

графической работы.

В этом случае поверхность Ф представляет собой множество

последовательных положений t1, t2,.. линии t , движение и форма которой

подчинены некоторому закону. Эту линию принято называть образующей.

По виду образующей различают поверхности линейчатые и нелинейчатые.

Образующей первых является прямая линия (конус, цилиндр), а вторых - кривая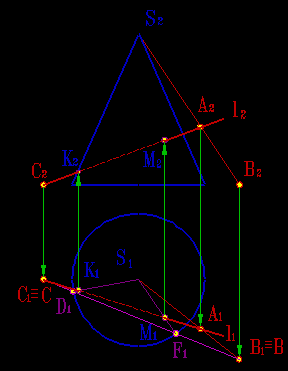

(сфера, тор). Линейчатые поверхности разделяют на развертывающиеся и

неразвертывающиеся.

К развертывающимся поверхностям относятся цилиндр и конус (прямые и

наклонные)

40 Цилиндр, конус, сфера. Сечение их плоскостью

Цилиндр-тело, которое описывает прямоугольник при вращении его около стороны как оси. Конус-тело, которое получено при вращении прямоугольного треугольника вокруг его катета как оси. Шар-тело полученное при вращении полукруга вокруг его диаметра как оси.

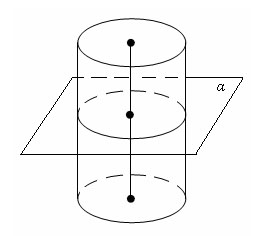
Сечение цилиндра плоскостью,параллельной его оси,представляет прямоугольник. Осевое сечение-сечение цилиндра плоскостью,проходящей через его ось.

Сечение цилиндра плоскостью, параллельной основаниям, представляет собой круг.

Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник. Осевое сечение конуса-это сечение, проходящее через его ось.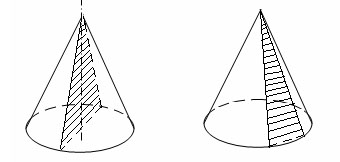

Сечение конуса плоскостью, параллельной его основаниям, представляет собой круг с центром на оси конуса.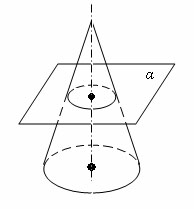

Сечение шара плоскостью есть круг. Центр этого шара есть основание перпендикуляра,опущенного из центра шара на секущую плоскость. Сечение шара диаметральной плоскостью называется большим кругом

41  При вращении окружности вокруг прямой, лежащей в плоскости образующей окружности, образуются торовые поверхности. Произвольная прямая пересекает тор в четырех точках, следовательно, это поверхность четвертого порядка.

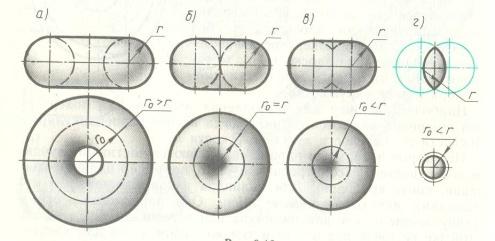
В зависимости от соотношения знаний радиуса образующей окружности R и расстояния r от центра окружности до оси вращения i возможны три разновидности поверхностей: Если R < r, то образующая окружность l не пересекает ось вращения i, поверхность называется кольцом или открытым тором. Если R > либо = R, то окружность касается оси или пересекает ее, поверхность называется закрытым тором. Если r = 0, то образуется сфера.

52-53

Алгоритм пересеченя прямой 1.Через прямую провести вспомогательную пл-ть. 2.Построить линию пересечения вспомогательной плоскости с пов-тью вращения 3.Найти точки пересечения заданной прямой с построенной линией пересечения