18Плоскость общего положения

Плоскость а, наклонная ко всем плоскостям проекций, называется плоскостью общего положения. Особенностью этой плоскости является то, что всякая кривая и фигура, лежащие в этой плоскости, при проектировании не имеют ни одной проекции, равной натуральной (истинной) величине.

19 Особые линии плоскости.

Прямая плоскости, параллельная к горизонтальной плоскости проекций, называется горизонталью этой плоскости. Прямая плоскости, параллельная к фронтальной плоскости проекций, называется фронталью этой плоскости. К особым линиям плоскости относят также линии наибольшего наклона плоскости к плоскостям проекций – это линии, лежащие в плоскости и перпендикулярные к горизонтали и фронтали плоскости. Линия наибольшего наклона к плоскости проекций П1 называется линией ската плоскости.

20Вращение вокруг линий уровня. Применение.

Любую геометрическую фигуру можно повернуть вокруг горизонтали или фронтали до положения, когда она станет параллельной П₁ или П₂, т.е. будет проецироваться на П₁ или П₂ в натуральную величину. Если вращение осуществляется вокруг горизонтали, то:

каждая точка фигуры перемещается по дугам окружностей, расположенных в плоскостях, перпендикулярных оси вращения и проецирующихся на П₁ в отрезки прямой, перпендикулярной горизонтальной проекции горизонтали;

центр окружности вращения лежит на горизонтали и горизонтальная проекция его определяется в пересечении горизонтальной проекции горизонтали и окружности вращения;

величина радиуса вращения равна расстоянию от точки до оси вращения.

21. Способ совмещения. Сущность способа и его применение.

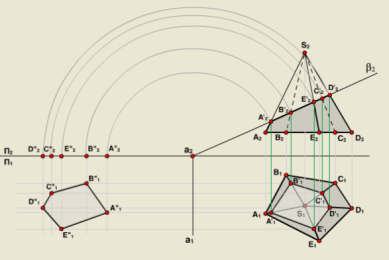
Для построения натурального размера сечения используем метод совмещения с горизонтальной плоскостью  проекций. Для совмещения фигуры сечения находящейся в проецирующей плоскости необходимо выполнить одно вращение.  Ось вращения   проведем через точку пересечения проекции с осью ОХ. (Ось может проходить и через другую точку лежащую на следе плоскости.) Проведем фронтальные проекции траекторий движения точек фигуры сечения. Новое фронтальное положение точки 1 это 1"2. Фронтальная проекция фигуры сечения стала параллельна оси ОХ и перпендикулярна линиям проекционной  связи. На горизонтальную плоскость фигура сечения спроецируется теперь в натуральную величину. Построим горизонтальную проекцию фигуры сечения на пересечении линий проекционной связи. Причем, если ось вращения перпендикулярна плоскости П2, то фронтальные проекции траекторий точек фигуры сечения будут представлять собой окружность, а горизонтальные - отрезки прямой.

22 Способ перемены плоскостей проекций. Сущность способа и его применение.

Суть способа заключается в том, что геометрический объект остается в пространстве неподвижным, а система плоскостей П₁ и П₂ дополняется плоскостями, образующими с П₁ или П₂ или между собой системы двух взаимно перпендикулярных плоскостей, по отношению к которым элементы геометрического объекта - частные положения.

Существующие при этом закономерности весьма не сложны и их можно проследить на примере одной точки

Первоначальный комплексный чертеж точки А образован ее проекциями на взаимно перпендикулярные плоскости П₁ и П₂, называемые в дальнейшем системой П₁-П₂. На комплексном чертеже наличие этой системы отмечено осью x₁₂, по обе стороны от которой обозначены поля проекций соответствующих плоскостей.

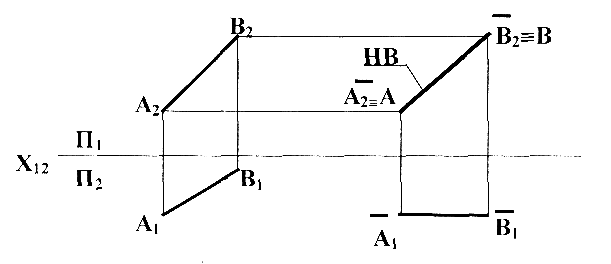
23Способ плоскопараллельного перемещения. Сущность способа и его применение. Суть способа заключается в том, что система плоскостей П₁ и П₂ остается неизменной, а сам геометрический элемент изменяет свое положение в пространстве.

Этот способ называют частным способом вращения вокруг проецируемой оси, или вращением без указания оси вращения.

Основным недостатком способа вращения является то, что новые проекции накладываются на старые - теряется наглядность комплексных чертежей.

Способ плоскопараллельного перемещения дает возможность устранить этот недостаток, сохраняя основные принципы вращения вокруг проецирующей оси:

одна проекция фигуры не меняет своей формы и размеров, а меняет лишь свое положение в пространстве;

все точки второй проекции перемещаются по прямым, параллельным оси X до пересечения с линиями связи, проведёнными из нового положения фигуры.

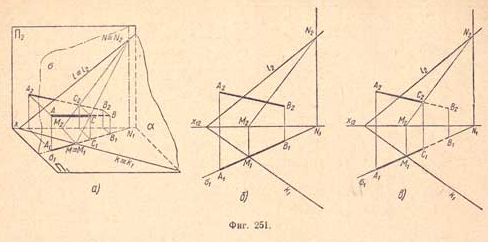
26Пересечение прямой с плоскостью общего положения. Пример 1. Даны: плоскость общего положения а и прямая общего положения АВ (А₁В₁ А₂В₂); требуется найти точку их пересечения (фиг.251,а). Проводим через прямуюАВ какую - либо вспомогательную плоскость, например горизонтально - проектирующую плоскость δ (δ₁), как показано на (фиг.251,б); она пересечет плоскостьa по прямой NM (N₁M₁, N₂М₂), которая, в свою очередь, пересечет прямую АВ (А₁В₁ А₂В₂) в точке С (С₁С₂), что видно на (фиг.251,в). Точ каС есть точка пересечения прямо й АВ с плоскостью а.

27Определение видимости

Точки, лежащие на одном проецирующем луче, называют конкурирующими точками. Конкурирующие точки конкурируют за условную ВИДИМОСТЬ на плоскостях проекций

.

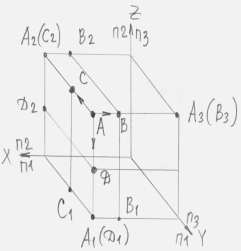
29Теперь рассмотрим пример пересечения двух плоскостей общего положения. Для построения линии пересечения двух плоскостей  и  необходимо найти две точки, N и M каждая из которых принадлежит обеим плоскостям. Для нахождения точек N и M можно воспользоваться следующим алгоритмом:

• Взять две дополнительные плоскости частного положения 1ЧП и 2ЧП;

• Определить линии пересечения плоскостей частного положения 1ЧП и 2ЧП с плоскостями общего положения  и  с помощью метода, приведенного в предыдущем пункте;

• Определить точки N и M пересечения полученных линий.

30Прямая параллельна плоскости, если эта прямая параллельна любой прямой в плоскости. Через заданную точку в пространстве можно провести бесчисленное множество прямых линий, параллельных заданной плоскости: Для получения единственного решения требуется какое-нибудь дополнительное условие. Если такую прямую в плоскости не удается построить, то заданные прямая и плоскость не параллельны между собой.

31Построение двух взаимно перпендикулярных плоскостей. Как известно, плоскости перпендикулярны, если прямая, принадлежащая одной плоскости, перпендикулярна другой плоскости. Поэтому плоскость, перпендикулярную к заданной, можно провести через прямую, перпендикулярную к заданной плоскости, или перпендикулярно прямой, лежащей в заданной плоскости.Построение:

1. Провести главные линии плоскости, С1 - горизонталь, С2 - фронталь.

2. Через произвольную точку Е (расположенную вне треугольника АВС) провести прямую EF перпендикулярно главным линиям плоскости (c₂f₂ перпендикулярна c₂2₂ и c₁f₁ перепендикулярна с₁1₁).

3. Через точку N провести произвольно прямую ЕМ, пересекающуюся с EF, получим плоскость Р заданную двумя пересекающимися прямыми(ЕМ Х EF).

Таким образом плоскость Р(МЕ Х EF) перепендикулярна плоскости Q(треугольник АВС).

Следует заметить, что у взаимно перпендикулярных плоскостей общего положения их одноименные следы никогда не перпендикулярны. Но если одна из заданных плоскостей (или обе) является плоскостью общего положения, то взаимная перпендикулярность на эпюре одной пары их следов свидетельствует о перпендикулярности плоскостей в пространстве.

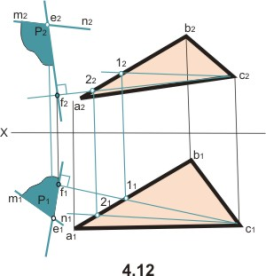
32Если прямая перпендикулярна плоскости, то горизонтальная проекция этой прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция – фронтальной проекции фронтали плоскости.

Пусть прямая n, перпендикулярная плоскости, пересекает плоскость BCD в точке N, тогда по условию n перпендикулярна любой прямой плоскости. Проведем в плоскости BCD горизонталь h, а на основании теоремы о проецировании прямого угла можно утверждать, что на горизонтальную плоскость проекций они проецируются под прямым углом, т.е. n₁ h₁. Аналогично для фронтали – f  n  f₂  n₂.

33-34Сечение многогранника плоскостью. Определение натуральной величины сечения.

Геометрическая фигура, получающаяся в результате пересечения многогранника плоскостью, называется сечением многогранника.

Сечение представляет собой плоский многоугольник с внутренней областью. В частном случае эти многоугольники могут распадаться на несколько многогранников, вырождаться в прямые и точки.  Сечение многогранника плоскостью можно построить двумя способами: 1. По точкам пересечения с плоскостью ребер многогранника.

2. По линиям пересечения граней многогранника с плоскостью. В первом случае задача сводится к определению точек пересечения прямой с плоскостью. Во втором случае - к определению линий пересечения плоскостей. В ряде случаев целесообразно комбинированное применение обоих способов.Определение натуральной величины сечения. Для нахождения истинной величины сечения необходимо преобразование чертежа. Построим истинную величину сечения многогранника способом совмещения или др.способами.