21. Теоремы Вейерштрасса для непрерывных функций на отрезке.

Функция непрерывна на отрезке, если она непрерывна во всех точках интервала и непрерывна справа в точкеи слева в точке.

Теорема (первая теорема Вейерштрасса).Если функция непрерывна на отрезке, то она ограничена на нем. (Необходимо доказать, что существует, что для всехвыполняется.).

Доказательство(от противного). Пусть для всякогонайдется такая точка, что: длянайдется; длянайдетсяи т. д..…длянайдетсяи т. д. Итак, построена последовательностьтакая, что для всех:. Ясно, что. Последовательность, т. е. ограничена. Следовательно, по теореме Больцано – Вейерштрасса (!!!!), существует подпоследовательностьтакая, что. Так как функциянепрерывна на отрезке, она непрерывна и в точке. Итак, имеем, но по построению, что является противоречием.

Пример.На интервале теорема, вообще говоря, неверна. Функциянепрерывна на, но не ограничена на нем.

Теорема (вторая теорема Вейерштрасса).Непрерывная функция на отрезкедостигает в некоторых точках отрезкасвоих точных верхней и нижней границ, т.е. существуюттакие,что

Доказательство. Докажем существование точки максимума функции , т.е. точки, в которой значение функции равно точной верхней грани множества значений функции. По предыдущей теореме(первая теорема Вейерштрасса) непрерывная на отрезке функцияявляется ограниченной на этом отрезке, следовательно, ограничена сверху, например, числом, т. е. для всех. Тогда существует точная верхняя границамножества значений функциина отрезке, т.е. такое число, что 1) для всех;

2) для любого существует точка. Возьмем последовательные значенияТогда построена последовательность. Эта последовательность ограничена. Следовательно, по теореме Больцано – Вейерштрасса (!!!!) из нее можно выделить подпоследовательностьтакую, что. Функциянепрерывна в точке.

Следовательно, , но, с другой стороны, для всехвыполняется. В силу свойства (Если для всехn и ,то)  сходящихся последовательностей заключаем, что . Итак,.

Замечание 6.2.1.Если функция разрывна, то теорема (вторая теорема Вейерштрасса), вообще говоря, неверна. Например,,(см. рис.). Значение, равное, функцией не достигается.

22. Теорема Больцано-Коши о нулях функции.

Теорема 6.2.3. Если функция непрерывна на отрезке, ее значения на концах отрезкаине равны нулю и имеют разные знаки, то на интервалеимеется по крайней мере одна точкатакая, что.

Доказательство (метод Больцано деления отрезка пополам). Пусть (см. рис.).

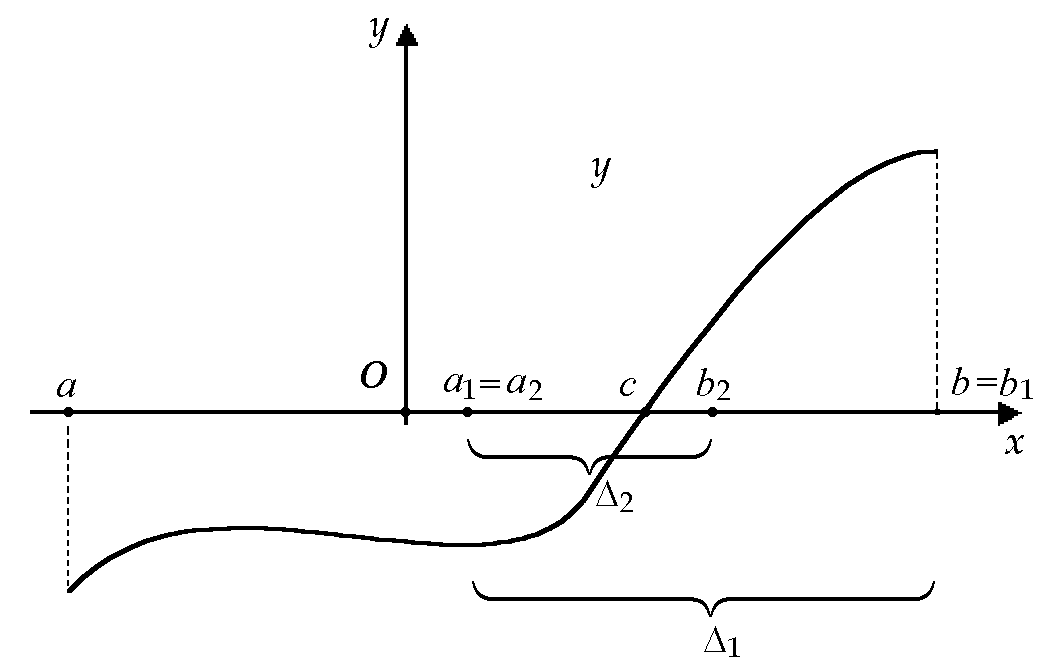
Обозначим отрезок . Разделим его пополам. Если в середине отрезкафункция равна нулю, то все доказано. Если нет, то обозначим зату из половин отрезка, на концах которой функцияимеет разные знаки:. Разделим отрезокпополам. Если в середине отрезкафункция равна нулю, то все доказано. Если нет, то обозначим зату из половин отрезка, на концах которой функцияимеет разные знаки:. Рассуждая таким образом, мы либо на каком-то шаге получим точку, в которой функция обращается в нуль, и все доказано, либо построим систему вложенных отрезков, длины которых стремятся к нулю, и для всехвыполняются неравенства. Следовательно, по теореме Кантора (Пусть задана система вложенных отрезков на, т. е. таких, что и длины отрезков при. Тогда существует, и притом единственная, точка, одновременно принадлежащая всем отрезкам.) существует точка , принадлежащая всем отрезкам. Поэтомуи. Тогда, с одной стороны,с другой стороны, в силу непрерывности функциив точке,Следовательно,.