
- •3. Единственность предела сходящейся последовательности
- •4. Ограниченность сходящейся последовательности.
- •5. Сохранение знака сходящейся последовательности
- •10.Арифметические свойства сходящихся последовательностей.
- •11. Теорема Кантора о вложенных отрезках.
- •12.Теорема Больцано-Вейерштрасса об ограниченных последовательностях.
- •13. Критерий Коши сходимости последовательности.
- •14.Теорема о существовании точных границ числовых множеств.
- •15. Принцип Бореля-Лебега.
- •16.Теорема Больцано-Вейерштрасса о существовании предельной точки у ограниченного числового множества.
- •17. Эквивалентность двух определений предела функции в точке.
- •19.Критерий Коши предела функции в точке.
- •20.Непрерывность сложной функции.
- •21. Теоремы Вейерштрасса для непрерывных функций на отрезке.
- •22. Теорема Больцано-Коши о нулях функции.
- •25. Теорема о существовании обратной функции.
- •26. Теорема о существовании и непрерывности обратной функции.
- •29. Непрерывность дифференцируемой функции.
- •30. Производная и дифференцируемость функции в точке.
- •31. Дифференцируемость функции в точке: правила дифференцирования, дифференцируемость сложной функции.
- •33. Теоремы о среднем: Ферма, Ролля, Лагранжа, Коши.
- •35. Первое правило Лопиталя.
- •36. Теорема Тейлора.
- •37. Достаточные условия экстремума.
13. Критерий Коши сходимости последовательности.
Из
определения сходимости последовательности
![]() к
точке
к
точке![]() вытекает,
что для любого
вытекает,
что для любого![]() интервалом
длиной
интервалом
длиной![]() можно
накрыть всю эту последовательность,
исключая, может быть, конечное число ее
элементов, если середину интервала
поместить в точку
можно
накрыть всю эту последовательность,
исключая, может быть, конечное число ее
элементов, если середину интервала
поместить в точку![]() .
Справедливо и обратное: если
последовательность
.
Справедливо и обратное: если
последовательность![]() такова,
что для любого
такова,
что для любого![]() можно
накрыть всю эту последовательность,
исключая, может быть, конечное число ее
элементов, поместив центр интервала в
некоторую точку, то она сходится.
Сформулируем это утверждение более
точно. Последовательность
можно
накрыть всю эту последовательность,
исключая, может быть, конечное число ее
элементов, поместив центр интервала в
некоторую точку, то она сходится.
Сформулируем это утверждение более
точно. Последовательность![]() назовемпоследовательностью
Коши
или фундаментальной,
если
назовемпоследовательностью
Коши
или фундаментальной,
если
![]() (здесь
центр интервала длиной
(здесь
центр интервала длиной![]() помещен
в точку
помещен
в точку![]()
![]() ,
см. рис.).
,
см. рис.).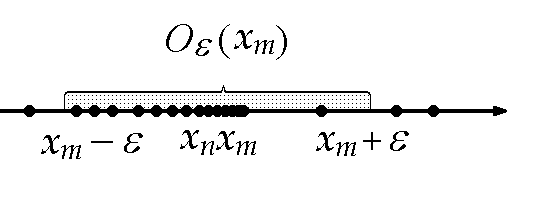
Теорема
(критерий Коши).Для того чтобы
последовательность
![]() сходилась,
необходимо и достаточно, чтобы она была
фундаментальной.
сходилась,
необходимо и достаточно, чтобы она была
фундаментальной.
Доказательство.
Необходимость(метод![]() ).
Пусть
).
Пусть![]() при
при![]() .
Тогда для любого
.
Тогда для любого![]() существует
номер
существует
номер![]() такой,что
для любых
такой,что
для любых![]() выполняются
неравенства
выполняются
неравенства![]()
![]() .
Рассмотрим цепочку соотношений
.
Рассмотрим цепочку соотношений
![]() что
означает, что
что
означает, что![]() фундаментальна.
фундаментальна.
Достаточность.Докажем сначала ограниченность
последовательности![]() .
Возьмем
.
Возьмем![]() ,
тогда, в силу фундаментальности
,
тогда, в силу фундаментальности![]() ,
найдется номер
,
найдется номер![]() такой,
что для всех
такой,
что для всех![]() выполняется
выполняется![]() .
Следовательно,
.
Следовательно,![]() ,
поэтому
,
поэтому![]() .
Итак, для всех
.
Итак, для всех![]() при
фиксированном
при
фиксированном![]() выполняется
выполняется![]() ,
что означает ограниченность
последовательности
,
что означает ограниченность
последовательности![]() (следует
из замечания: последовательность
(следует
из замечания: последовательность![]() будет
ограниченной, если ее можно накрыть
отрезком
будет
ограниченной, если ее можно накрыть
отрезком![]() ,
начиная с некоторого номера
,
начиная с некоторого номера![]() ).
Потеореме
Больцано-Вейерштрассаоб
ограниченных последовательностях из
последовательности
).
Потеореме
Больцано-Вейерштрассаоб
ограниченных последовательностях из
последовательности![]() можно
выделить подпоследовательность
можно
выделить подпоследовательность![]() ,
сходящуюся к некоторому числу
,
сходящуюся к некоторому числу![]() .
Докажем, что и вся последовательность
.
Докажем, что и вся последовательность![]() сходится
к числу
сходится
к числу![]() .
Возьмем любое
.
Возьмем любое![]() ,
тогда найдется номер
,
тогда найдется номер![]() (изфундаментальности
(изфундаментальности![]() )
такой, что для всех
)
такой, что для всех![]() выполняется
выполняется![]() .
Ввиду сходимости
.
Ввиду сходимости![]() при
при![]() ,
по взятому
,
по взятому![]() найдется
номер
найдется
номер![]() такой,
что
такой,
что![]() и
и![]() .
Тогда для нашего
.
Тогда для нашего![]()
![]()
![]()
что означает
сходимость последовательности
![]() к
числу
к
числу![]() .
.
14.Теорема о существовании точных границ числовых множеств.
Множество
![]() называетсяограниченным
сверху, если существует число
называетсяограниченным
сверху, если существует число![]() такое,
что для всех
такое,
что для всех![]() .
Число
.
Число![]() называетсяверхней границей(мажорантой)
множества
называетсяверхней границей(мажорантой)
множества![]() .
.
Точной
верхней границеймножества![]() называется
число
называется
число![]() такое,
что
такое,
что
1)
![]() (т.е.
(т.е.![]() --
одна из верхних границ множества
--
одна из верхних границ множества![]() );
);
2)
![]() (т.е.
границу
(т.е.
границу![]() множества
множества![]() нельзя
уменьшить).
нельзя
уменьшить).
Точная
верхняя граница множества
![]() обозначается
обозначается![]() .
Аналогично определяется точная нижняя
граница множества, которую обозначают
.
Аналогично определяется точная нижняя
граница множества, которую обозначают![]() :
:
1)
![]() (т.е.
(т.е.![]() --
одна из нижних границ множества
--
одна из нижних границ множества![]() );
);
2)
![]() (т.е.
границу
(т.е.
границу![]() множества
множества![]() нельзя увеличить).
нельзя увеличить).
Теорема.Если непустое множество действительных чисел ограничено сверху, то существует точная верхняя граница этого множества.
Доказательство(метод Больцано - метод деления отрезка
пополам). Пусть![]() и
множество
и
множество![]() ограничено
сверху числом
ограничено
сверху числом![]() .
Рассмотрим отрезок
.
Рассмотрим отрезок![]() ,
заметим, что правее
,
заметим, что правее![]() нет
точек из
нет
точек из![]() .
Разделим отрезок на два равных отрезка
и обозначим
.
Разделим отрезок на два равных отрезка
и обозначим![]() самый
правый из них, содержащий хотя бы одну
точку из
самый
правый из них, содержащий хотя бы одну
точку из![]() ,
т. е. правее
,
т. е. правее![]() нет
точек из
нет
точек из![]() .
Так же поступим с отрезком
.
Так же поступим с отрезком![]() ,
получим отрезок
,
получим отрезок![]() ,
содержащий хотя бы одну точку из
,
содержащий хотя бы одну точку из![]() ,
правее которого нет точек из
,
правее которого нет точек из![]() .
Продолжив этот процесс по индукции,
получим последовательность отрезков
.
Продолжив этот процесс по индукции,
получим последовательность отрезков![]() ,
длины которых
,
длины которых![]() .
При этом при любом
.
При этом при любом![]() правее
правее![]() нет
точек из
нет
точек из![]() .
На основании принципа вложенных отрезков(Пусть
задана система вложенных отрезков
.
На основании принципа вложенных отрезков(Пусть
задана система вложенных отрезков
![]() на
на![]() ,
т. е. таких, что
,
т. е. таких, что![]() и длины отрезков
и длины отрезков![]() при
при![]() .
Тогда существует, и притом единственная,
точка, одновременно принадлежащая всем
отрезкам
.
Тогда существует, и притом единственная,
точка, одновременно принадлежащая всем
отрезкам![]() )
существует единственная точка
)
существует единственная точка![]() ,
лежащая во всех отрезках системы
,
лежащая во всех отрезках системы![]() .
.
Докажем,
что
![]() .
В самом деле, по построению для всех
.
В самом деле, по построению для всех![]() и
для всех
и
для всех![]() выполняется
неравенство
выполняется
неравенство![]() .
Тогда, переходя к пределу в этом
неравенстве при
.
Тогда, переходя к пределу в этом
неравенстве при![]() ,
получим (используя то, что
,
получим (используя то, что![]() )
неравенство
)
неравенство![]() .
Возьмем теперь любое
.
Возьмем теперь любое![]() .
Тогда (так как и
.
Тогда (так как и![]() )
существует номер
)
существует номер![]() такой,
что
такой,
что![]() лежит
левее отрезка
лежит
левее отрезка![]() .
При этом в
.
При этом в![]() лежит
хотя бы одна точка
лежит
хотя бы одна точка![]() ,
т.е. выполняется неравенство
,
т.е. выполняется неравенство![]() .
Следовательно,
.
Следовательно,![]() .
.
Будем
считать в дальнейшем, что если множество
![]() неограничено
сверху, то
неограничено
сверху, то![]() ,
если неограничено снизу, то
,
если неограничено снизу, то![]() .
.
