
- •3. Единственность предела сходящейся последовательности
- •4. Ограниченность сходящейся последовательности.
- •5. Сохранение знака сходящейся последовательности
- •10.Арифметические свойства сходящихся последовательностей.
- •11. Теорема Кантора о вложенных отрезках.
- •12.Теорема Больцано-Вейерштрасса об ограниченных последовательностях.
- •13. Критерий Коши сходимости последовательности.
- •14.Теорема о существовании точных границ числовых множеств.
- •15. Принцип Бореля-Лебега.
- •16.Теорема Больцано-Вейерштрасса о существовании предельной точки у ограниченного числового множества.
- •17. Эквивалентность двух определений предела функции в точке.
- •19.Критерий Коши предела функции в точке.
- •20.Непрерывность сложной функции.
- •21. Теоремы Вейерштрасса для непрерывных функций на отрезке.
- •22. Теорема Больцано-Коши о нулях функции.
- •25. Теорема о существовании обратной функции.
- •26. Теорема о существовании и непрерывности обратной функции.
- •29. Непрерывность дифференцируемой функции.
- •30. Производная и дифференцируемость функции в точке.
- •31. Дифференцируемость функции в точке: правила дифференцирования, дифференцируемость сложной функции.
- •33. Теоремы о среднем: Ферма, Ролля, Лагранжа, Коши.
- •35. Первое правило Лопиталя.
- •36. Теорема Тейлора.
- •37. Достаточные условия экстремума.
3. Единственность предела сходящейся последовательности
Последовательность
![]() называется
сходящейся,
если существует число
называется
сходящейся,
если существует число![]() ,
к которому она сходится, т.е.
,
к которому она сходится, т.е.![]() Иногда
удобно записывать определение сходимости
последовательности
Иногда
удобно записывать определение сходимости
последовательности![]() в
следующих эквивалентных первоначальному
видах:
в
следующих эквивалентных первоначальному
видах:![]()
![]()
![]() вне
окрестности
вне
окрестности![]() лежит
конечное число элементов последовательности
лежит
конечное число элементов последовательности![]() .
.
Теорема.
Если последовательность
![]() сходится,
то ее предел единственный.
сходится,
то ее предел единственный.
Доказательство
(от противного). Пусть
![]() .
Возьмем
.
Возьмем![]() ,
тогда
,
тогда![]() по
выбору
по
выбору![]() ,
с другой стороны, по определению
сходимости, для
,
с другой стороны, по определению
сходимости, для![]()
![]()
![]()
Следовательно,
для
![]() ,
что означает непустоту этого пересечения.
Получено противоречие.
,
что означает непустоту этого пересечения.
Получено противоречие.
4. Ограниченность сходящейся последовательности.
Последовательность
![]() называетсяограниченной,
если
называетсяограниченной,
если![]() .
Это означает, что
.
Это означает, что![]() или
что множество
или
что множество![]() можно
накрыть отрезком
можно
накрыть отрезком![]() .
.
Замечание.Ясно, что последовательность![]() будет
ограниченной, если ее можно накрыть
отрезком
будет
ограниченной, если ее можно накрыть
отрезком![]() ,
начиная с некоторого номера
,
начиная с некоторого номера![]() .
(Вне отрезка
.
(Вне отрезка![]() может
лежать лишь конечное число элементов
последовательности
может
лежать лишь конечное число элементов
последовательности![]() ,
следовательно, и всю последовательность
можно накрыть некоторым отрезком
,
следовательно, и всю последовательность
можно накрыть некоторым отрезком![]() ,
где
,
где![]() ).
).
Теорема.Если последовательность сходится, то она ограничена.
Доказательство.Пусть![]() и
и![]() .
Тогда, по определению сходимости,
существует номер
.
Тогда, по определению сходимости,
существует номер![]() такой,
что для всех
такой,
что для всех![]() .
Следовательно,
.
Следовательно,![]() ,
и поэтому
,
и поэтому![]() .
Итак, позамечанию,
последовательность
.
Итак, позамечанию,
последовательность![]() ограничена.
ограничена.
5. Сохранение знака сходящейся последовательности
Теорема.Если последовательность
![]() сходится
к числу
сходится
к числу![]() ,
то вся последовательность
,
то вся последовательность![]() лежит
вне окрестности нуля
лежит
вне окрестности нуля![]() (радиус
а/2), начиная с некоторого номера.(Другая
формулировка теоремы:ana>0,тогда
(радиус
а/2), начиная с некоторого номера.(Другая
формулировка теоремы:ana>0,тогда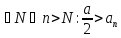 )
)
Доказательство.Достаточно взять![]() .
Тогда, по определению предела, найдется
.
Тогда, по определению предела, найдется![]() ,
что для всех
,
что для всех![]() ,
следовательно,
,
следовательно,![]()
6.Теорема о переходе к пределу в неравенстве для двух последовательностей.
Свойство
3.2.4.
Если
![]() для
всехn
и
для
всехn
и
![]() ,
то
,
то![]() Доказательство.
Пусть, напротив,
Доказательство.
Пусть, напротив,
![]() .
Зададим
.
Зададим![]() .
Тогда по определению сходимости
.
Тогда по определению сходимости![]()
![]()
Следовательно,
для
![]() выполняются
соотношения
выполняются
соотношения
![]() что
противоречит условию теоремы.
что
противоречит условию теоремы.
7.Теорема о трех последовательностях.
Теорема.
Если
![]() для
всехn
и
для
всехn
и
![]() ,то
,то![]()
Доказательство.
Проверим, что выполняется определение
сходимости последовательности
![]() к
числу
к
числу![]() .
Возьмем любое
.
Возьмем любое![]() ,
тогда из условия
,
тогда из условия![]() следует,
что
следует,
что![]() из условия
из условия![]() следует,
что
следует,
что![]() Поэтому для всех
Поэтому для всех![]() выполняются
неравенства
выполняются
неравенства![]() следовательно,
следовательно,![]() .
.
Пример 3.2.1.Докажем, что![]() .
Действительно, для любого
.
Действительно, для любого![]() ,
получим
,
получим
![]() Следовательно,
Следовательно,![]() .
.
8. Связь между бесконечно малыми и бесконечно большими последовательностями.
Последовательность
![]() называетсябесконечно
малой,
если
называетсябесконечно
малой,
если
![]() при
при![]() .
Развернутое определение:
.
Развернутое определение:![]()
Последовательность
![]() называетсябесконечно
большой,
если
называетсябесконечно
большой,
если
![]() Этот факт будем записывать так:
Этот факт будем записывать так:![]() при
при![]() или
или![]()
Теорема
3.3.1.Последовательность
![]() является
бесконечно малой последовательностью
тогда и только тогда, когда последовательность
является
бесконечно малой последовательностью
тогда и только тогда, когда последовательность![]() является
бесконечно большой.
является
бесконечно большой.
Доказательствоследует из того факта, что неравенство![]() равносильно
неравенству
равносильно
неравенству![]() ,
и определений бесконечно малых и
бесконечно больших последовательностей.
(Берем
,
и определений бесконечно малых и
бесконечно больших последовательностей.
(Берем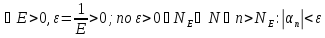
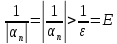 )
)
9.Свойства бесконечно малых последовательностей.
Свойство
1.
Сумма
и разность бесконечно малых
последовательностей
![]() и
и![]() есть
бесконечно малая последовательность.
есть
бесконечно малая последовательность.
Доказательство.
Возьмем произвольное
![]() .
Для него
.
Для него![]()
![]() Тогда
Тогда![]()
Свойство
2.
Произведение
![]() бесконечно
малой последовательности
бесконечно
малой последовательности![]() на
ограниченную последовательность
на
ограниченную последовательность![]() есть
бесконечно малая последовательность.
Доказательство.
Из ограниченности
есть
бесконечно малая последовательность.
Доказательство.
Из ограниченности
![]() следует
существование числа
следует
существование числа![]() такого,
что для всех
такого,
что для всех![]() .
Следовательно, при любом положительном
.
Следовательно, при любом положительном![]() для
положительного
для
положительного![]() существует
номер
существует
номер![]() такой,
что для всех
такой,
что для всех![]() .
Поэтому для этихn>N
имеем
.
Поэтому для этихn>N
имеем![]() .
Следовательно, по определению Коши,
.
Следовательно, по определению Коши,![]() при
при![]() .
.
Свойство
3.
Для
того чтобы последовательность
![]() была
сходящейся, необходимо и достаточно,
чтобы существовали число
была
сходящейся, необходимо и достаточно,
чтобы существовали число![]() и
бесконечно малая последовательность
и
бесконечно малая последовательность![]() такие,
что для всех
такие,
что для всех![]() выполнялось
равенство
выполнялось
равенство![]() .
.
Доказательство.
Необходимость.
Пусть
![]() при
при![]() .
Рассмотрим
.
Рассмотрим![]() ,
тогда из определения сходимости
,
тогда из определения сходимости![]() следует,
что
следует,
что![]() при
при![]() .
.
Достаточность.
Если
![]() ,
то из того, что
,
то из того, что![]() - бесконечно малая последовательность
и
- бесконечно малая последовательность
и![]() следует,
что
следует,
что![]() при
при![]() .
.
