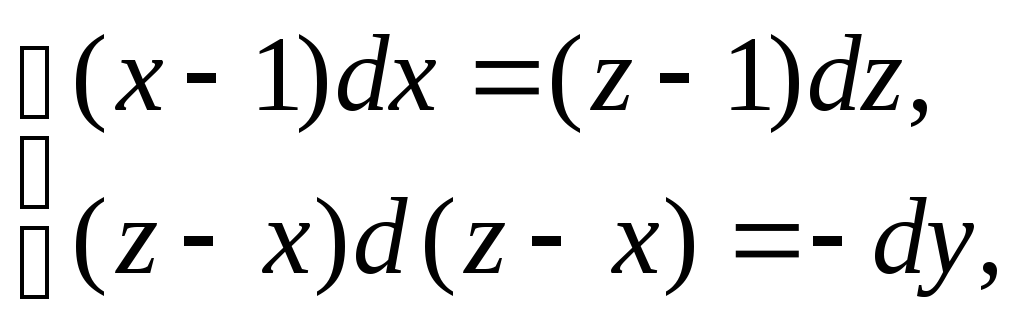ПП_27_Диф_Ур 4
.docПП 27 системы дифференциальных уравнений
|
№ п/п |
ЗАДАЧИ ПП 27 1. Метод исключения неизвестных |
Ответ |
|
|
№ 1 |
Решите задачу Коши для системы дифференциальных уравнений
Решение: Метод
исключения
неизвестных
позволяет свести систему дифференциальных
уравнений для двух неизвестных функций
Дифференцируя первое уравнение системы и заменяя у с помощью второго уравнения системы, получим подставим в предыдущее уравнение, получим - НЛДУ 2-го порядка с постоянными коэффициентами. Решим НЛДУ методом неопределенных коэффициентов. 1)
Находим общее решение
Характеристическое
уравнение
2)
Находим частное решение
3) Общее решение уравнения имеет вид:
Вторую
неизвестную функцию
Общее решение системы имеет вид: Решение задачи Коши: |
|
|
|
№ 2 |
Найдите
решение системы
Решение:
Продифференцируем
первое уравнение:
Его решение
|
|
|
|
№ 3 |
Решите
систему
Решение:
Дважды
продифференцируем первое уравнение
подставим
во второе
|
|
|
|
№ 4 |
Найдите
решение системы:
Решение: Перепишем систему в других обозначениях:
Продифференцируем
первое уравнение
Из первого уравнения найдем
|
|
|
|
№ 5 |
Найдите
решение системы
Решение:
|
|
|
|
2. Метод интегрируемых комбинаций |
|||
|
№ 6 |
Решите
систему:
Решение: Складывая почленно уравнения системы, получаем
Вычитая уравнения, получаем
Из
системы
|
|
|
|
№ 7 |
Решите
систему:
Решение: Составим интегрируемые комбинации:
Решением
системы является линия пересечения
поверхностей:
|
|
|


 ,
,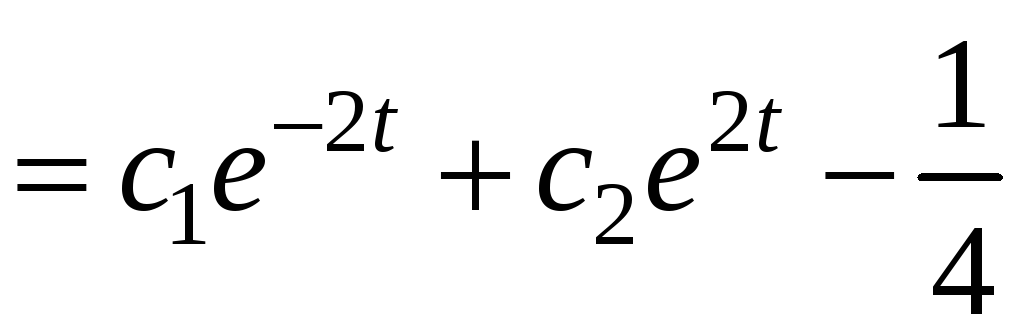 .
. .
. Для
решения задачи Коши подставим начальные
условия
Для
решения задачи Коши подставим начальные
условия
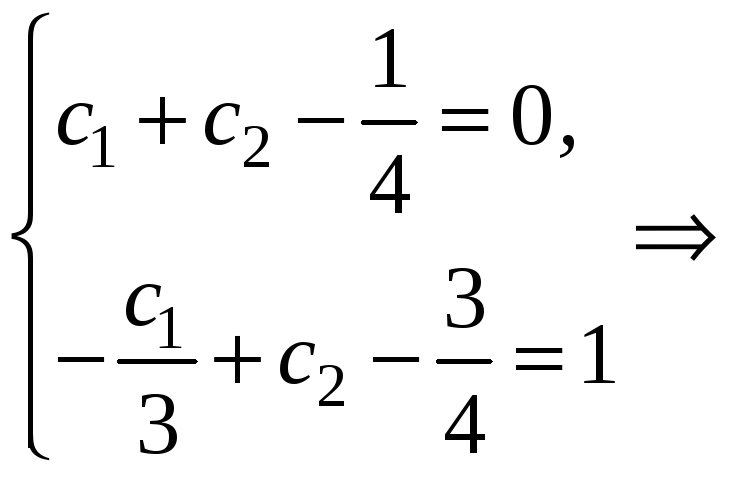
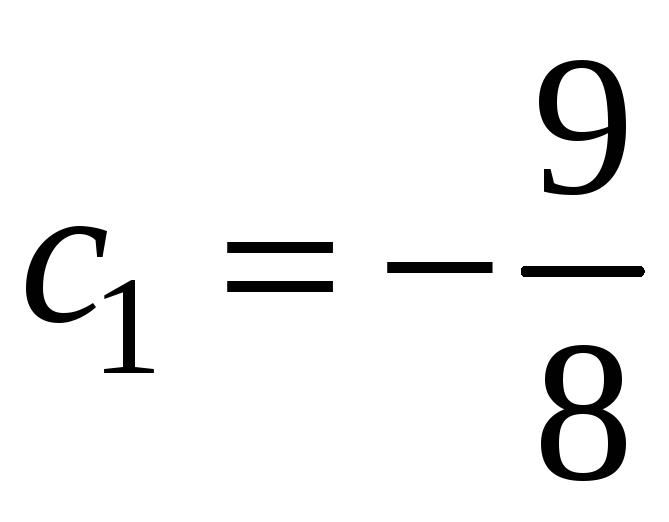 ,
,
 .
.


 ;
подставим
;
подставим
 ;
получим
НЛДУ второго порядка для
;
получим
НЛДУ второго порядка для
 .
.
 .
.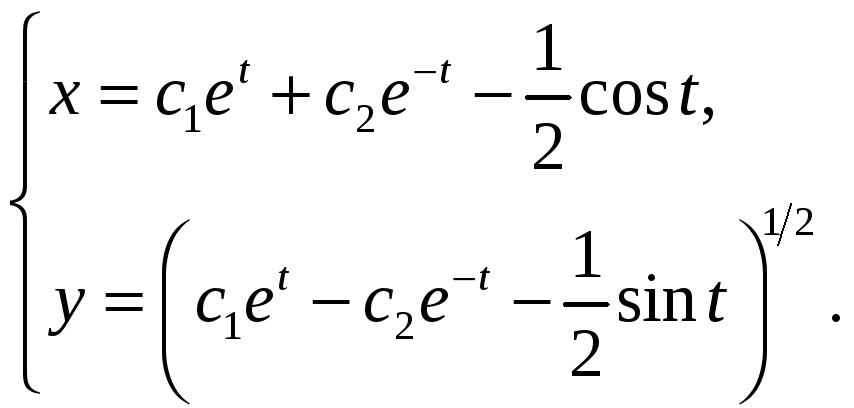

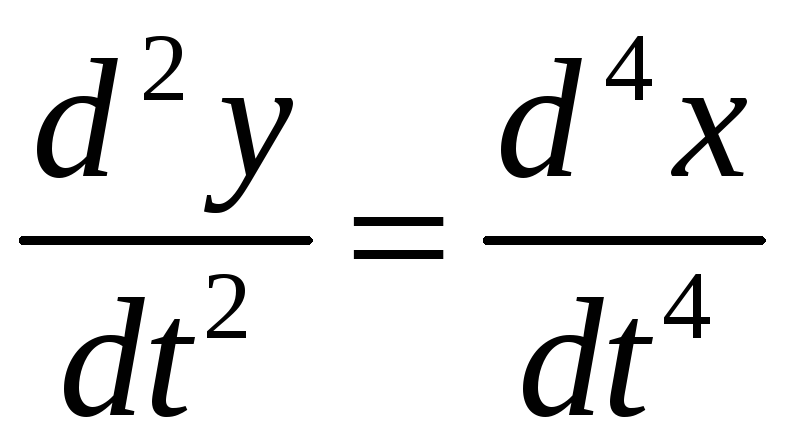 ,
,
 ,
,


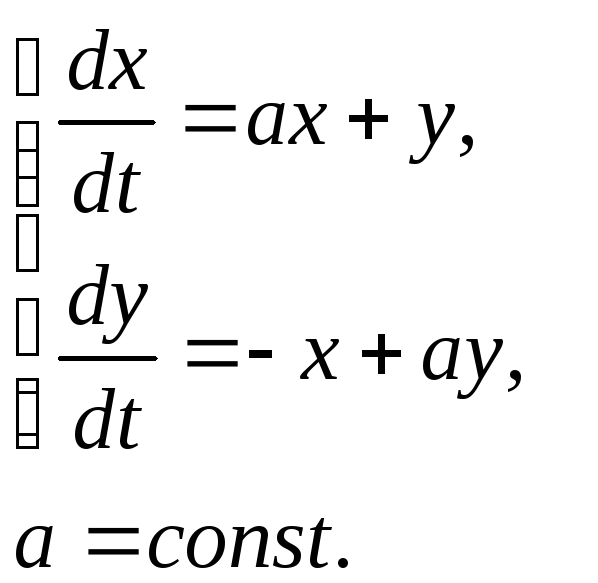
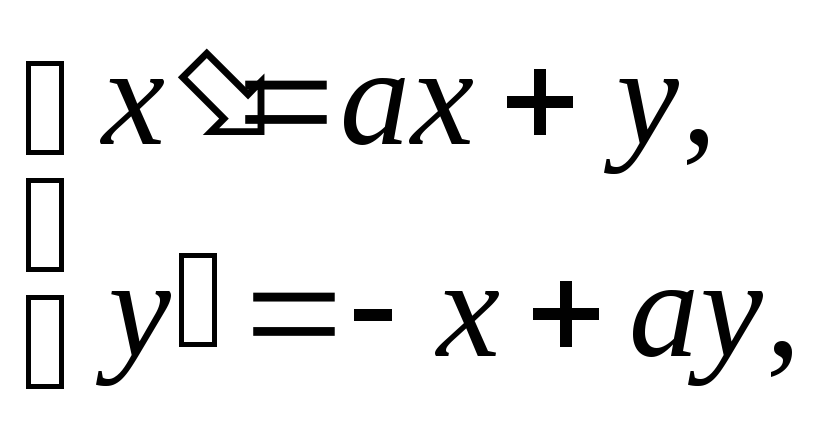 где
где
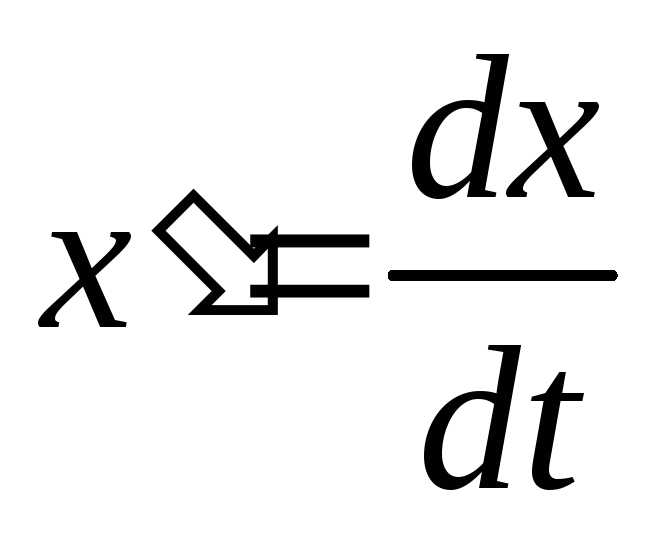 ,
,
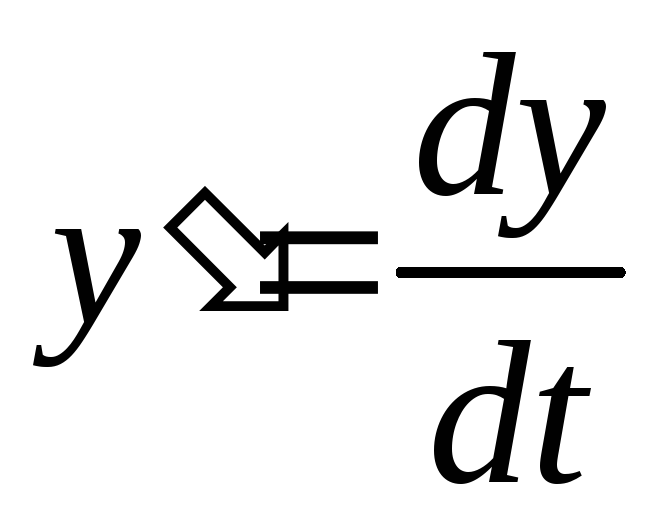 .
.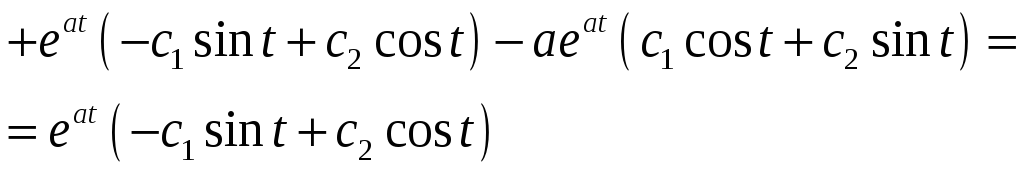 .
.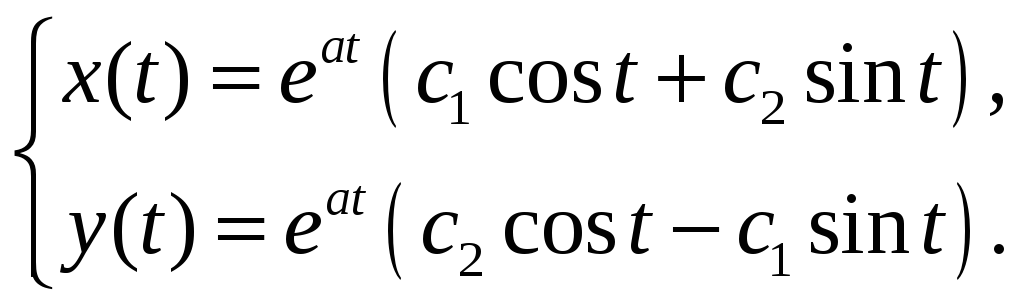


 .
.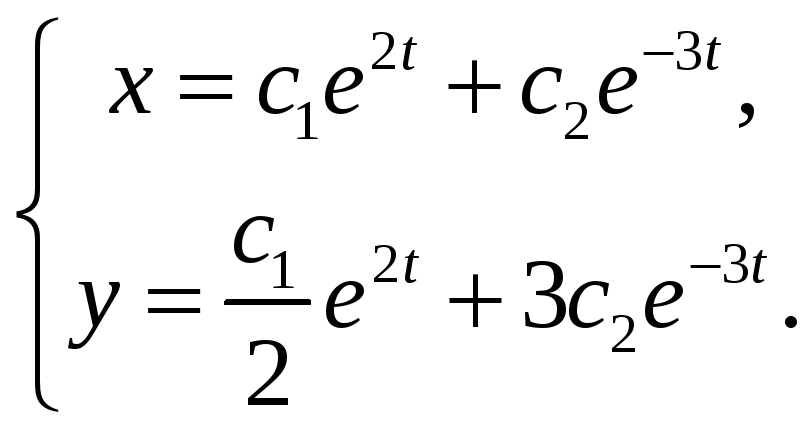

 .
.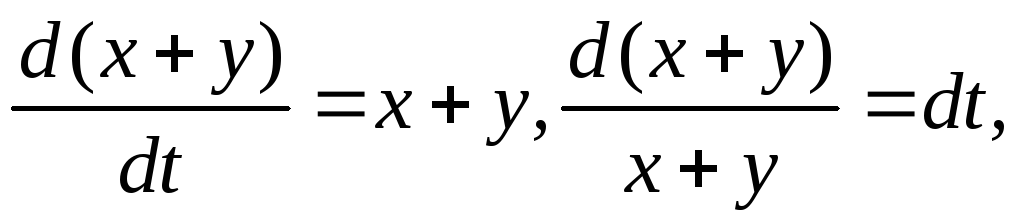
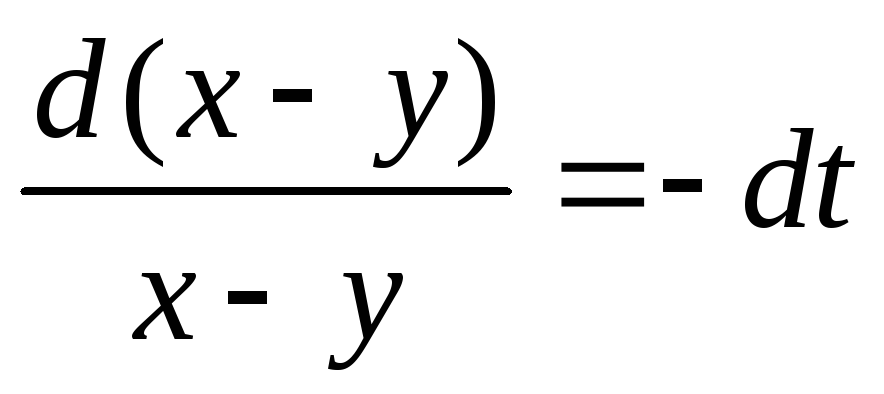 ,
,
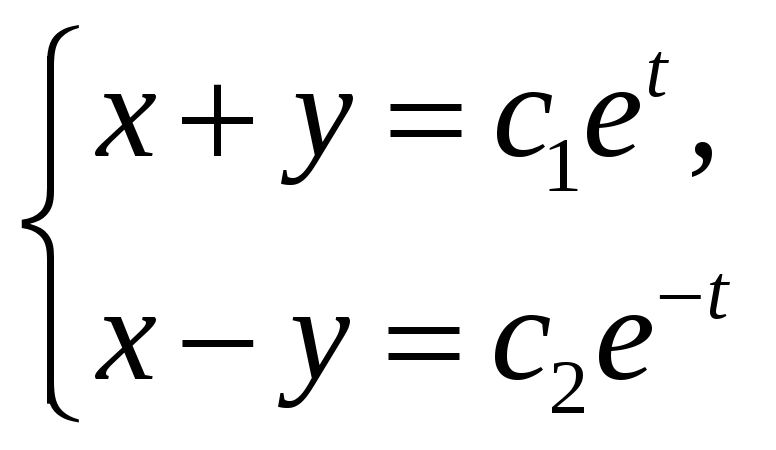 получаем решение в виде:
получаем решение в виде:


 .
.