
ПП_24_Диф_Ур 1
.docПП 24 дифференциальные уравнения (ДУ)
I. ДУ первого порядка
1. Решения ДУ первого порядка
|
Вид уравнения |
Тип уравнения |
Метод решения |
|
1.
|
с разделяющимися переменными |
непосредственное интегрирование |
|
2.
|
однородное |
|
|
3.
|
обобщенное однородное |
|
|
4.
|
линейное
по
|
|
|
5.
|
линейное
по
|
|
|
6.
|
Бернулли |
|
|
7.
|
уравнение в полных дифференциалах |
интегрирование
системы
|
|
№ п/п |
ЗАДАЧИ ПП 24 1. ДУ с разделяющимися переменными |
Ответ |
|
№ 1 |
Найдите
решение ДУ
Решение:
Решение
ДУ:
|
|
|
№ 2 |
Найдите
общий интеграл дифференциального
уравнения
Решение: Группируем члены, содержащие dx и dy:
- уравнение с разделенными переменными. Интегрируя, находим:
Общий
интеграл ДУ:
|
|
|
|
2. Однородные ДУ первого порядка |
|
|
№ 3 |
Найдите
общий интеграл дифференциального
уравнения
Решение:
Поделив
числитель и знаменатель правой части
на
Подставим:
Получим
для
- уравнение с разделяющимися переменными. Интегрируя,
получаем
С
учетом подстановки
Общий интеграл ДУ:
|
|
|
№ 4 |
Найдите
решение ДУ
Решение:
Решение
ДУ:
|
|
|
№ 5 |
Найдите
решение ДУ
Решение: ДУ – обобщенное однородное. Найдем
Решим однородное ДУ
Подстановкой
в предыдущее уравнение убеждаемся,
что значения
Кроме
того
Общий интеграл:
В старых переменных общее решение имеет вид:
Частные
решения
|
|
|
|
3. Линейные ДУ первого порядка |
|
|
№ 6 |
Найдите
решение ДУ
Решение:
ДУ
– линейное по
Ищем
решение в виде: ДУ
для
ДУ
для
Общее
решение:
|
|
|
№ 7 |
Найдите решение задачи Коши для ДУ
Решение:
ДУ
– линейное по
Ищем
решение в виде:
Найдем
любое нетривиальное частное решение
уравнения с разделяющимися переменными
для
Его общее решение:
Выберем
С = 0, тогда
Подставим
Интегрируя, получаем
Общее решение уравнения имеет вид
Учитывая
начальное условие
Решение
задачи Коши имеет вид
|
|
|
№ 8 |
Решите задачу Коши
Решение: ДУ – линейное по х (у):
Ищем
решение в виде:
Уравнение принимает вид
Находим
любое нетривиальное частное решение
уравнения с разделяющимися переменными
для
Подставим
Вычислим
Аналогично,
Общее решение уравнения имеет вид:
Учитывая
начальное условие
Решение задачи Коши имеет вид:
или
|
|
|
|
4. ДУ Бернулли |
|
|
№ 9 |
Найдите
решение ДУ
Решение:
Умножим
на
Сделаем
замену переменной:
тогда
Ищем
решение в виде:
ДУ
для
ДУ
для
Общее
решение:
|
|
|
№ 10 |
Найдите решение задачи Коши
Решение:
Сразу
ищем решение в виде:
Имеем
Найдем
любое частное решение уравнения с
разделяющимися переменными для
Его
общее решение:
Выберем
С
= 0, получим,
Подставляем
Общее решение уравнения: Учитывая
начальное условие
При
разделении переменных в уравнении
для
было
потеряно решение
Заметим,
что решение
Значит, |
|
|
|
5. ДУ в полных дифференциалах |
|
|
№ 11 |
Решите
ДУ
Решение: Уравнение
имеет вид
1)
Вычислим
2)
3)
4)
5)
6)
Общий
интеграл ДУ:
|
|
|
№ 12 |
Найдите общий интеграл уравнения
Решение:
Уравнение
имеет вид
Представим
Р
и Q
в виде
Для определения u имеем систему уравнений Интегрируя первое уравнение системы, получаем
Для
определения неизвестной функции
Интегрируя это уравнение с разделяющимися переменными, получаем Подставим
полученную функцию
Общий интеграл уравнения: |
|
|
№ 13 |
Решите
ДУ
Решение:
(поиск
особого
решения ДУ)
|
|

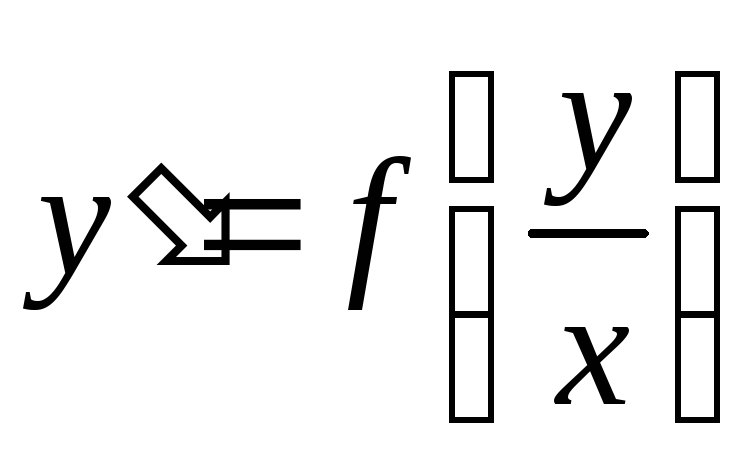
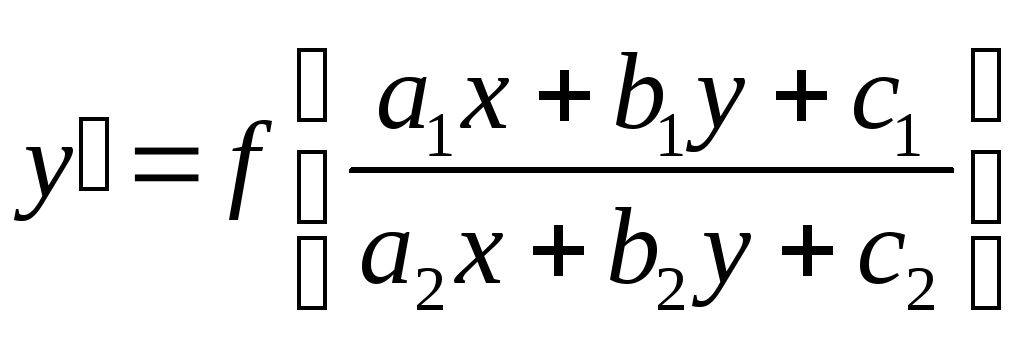

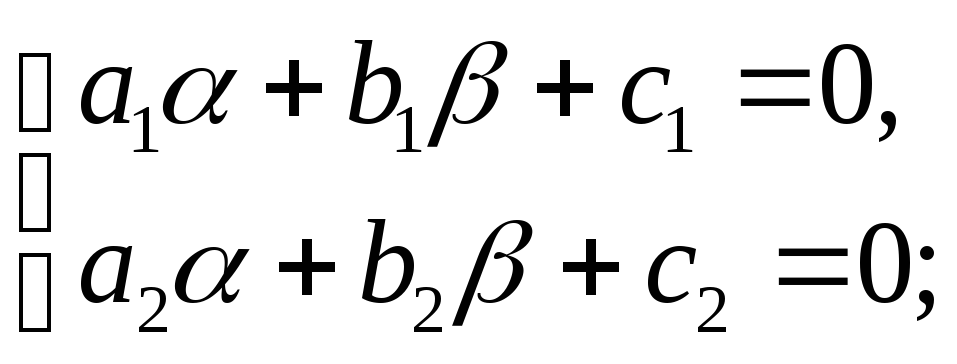
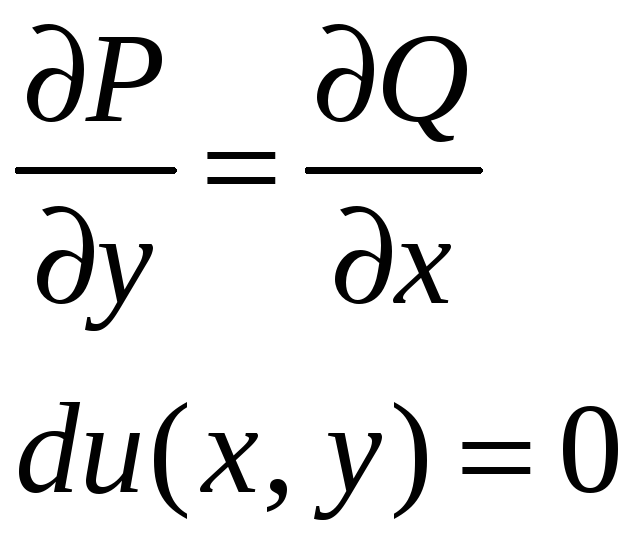


 ,
,
 ,
,

 ,
,
 .
.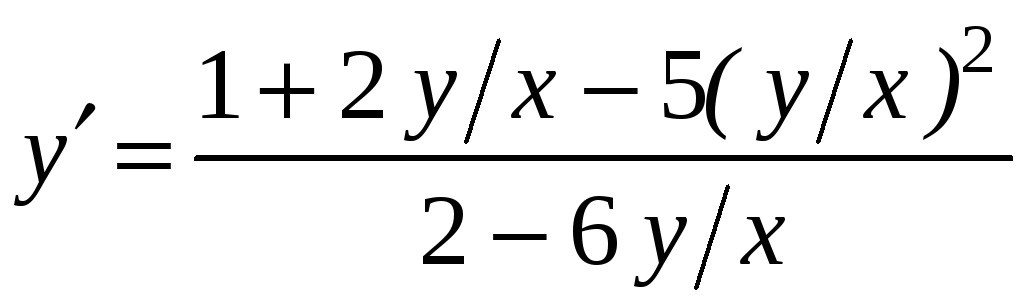 .
.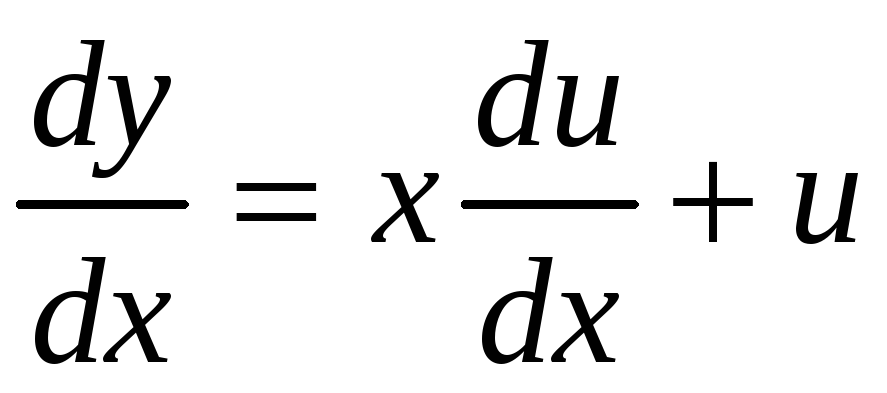 .
.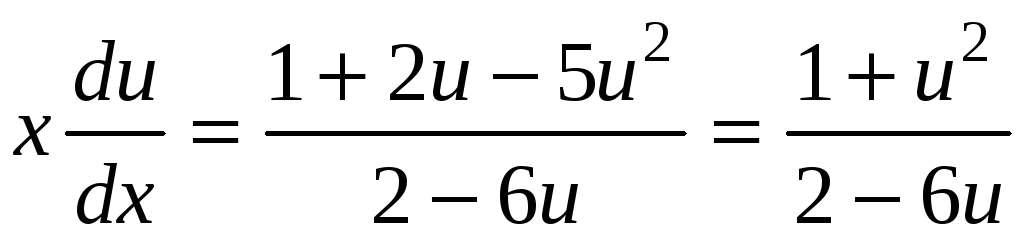 ,
,
 .
.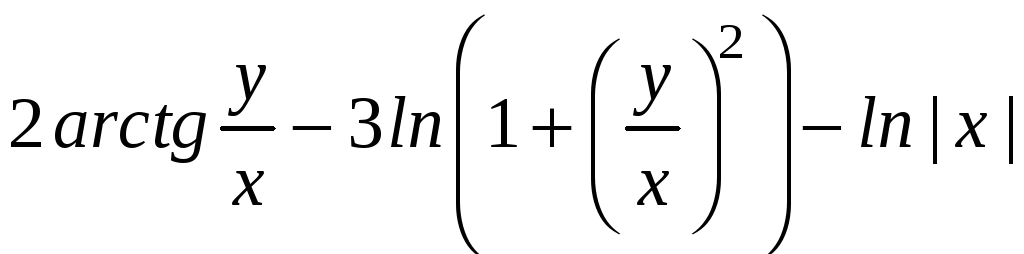 =С.
=С.
 .
.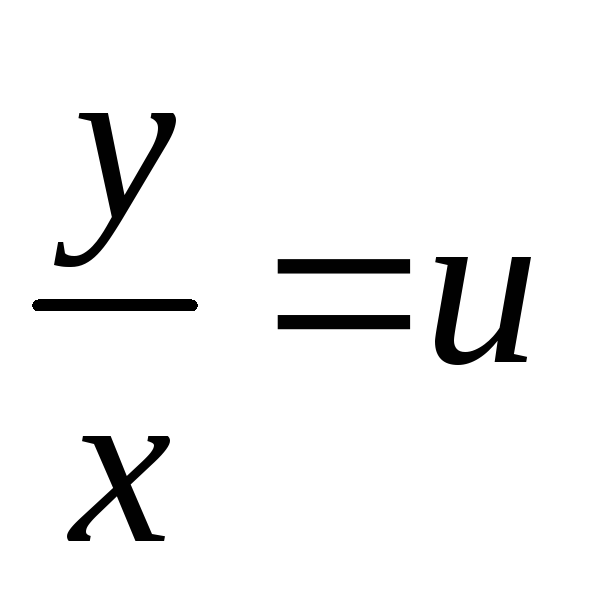 ,
,
 .
.
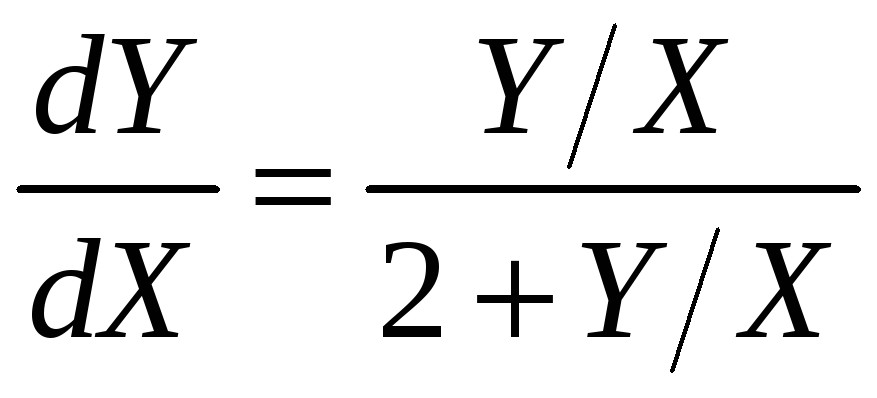 при
при
 .
. ,
,
 ,
,


 ,
,
 ,
,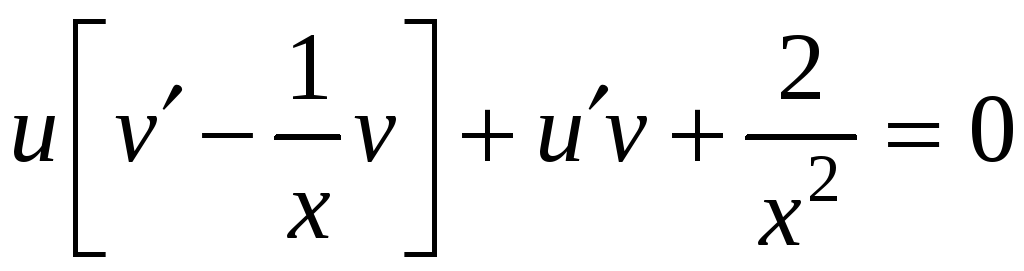 .
.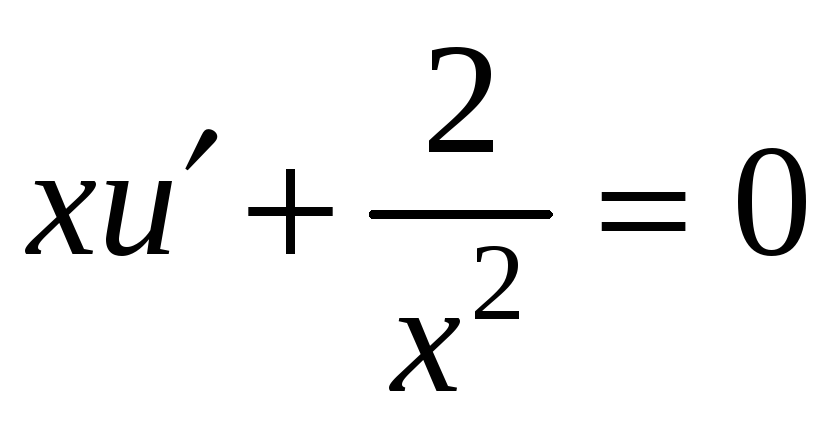 .
. .
. .
. .
.
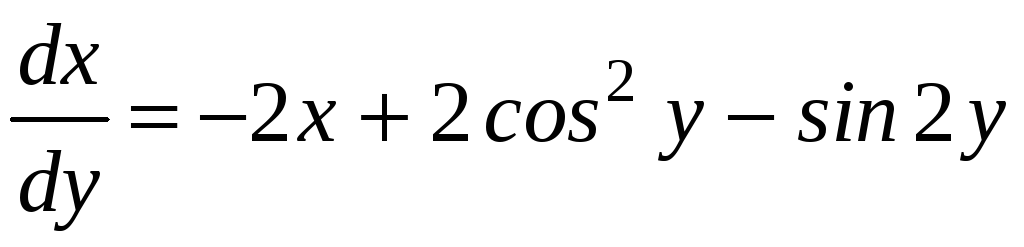 ,
,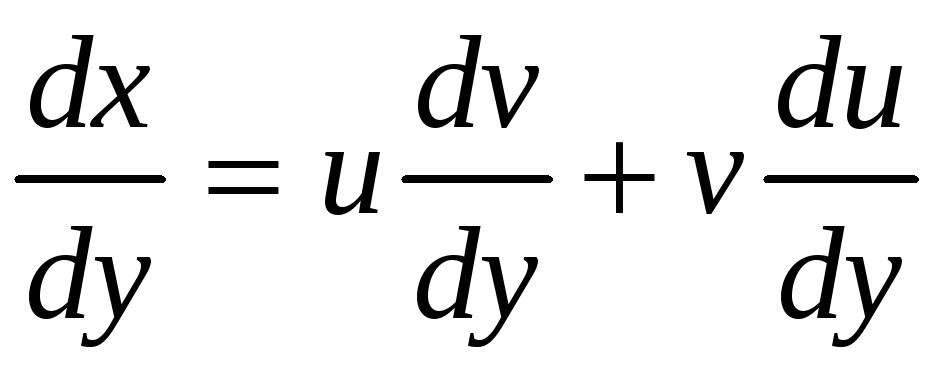 .
. ,
, .
. ,
например,
,
например,
 .
. ;
;

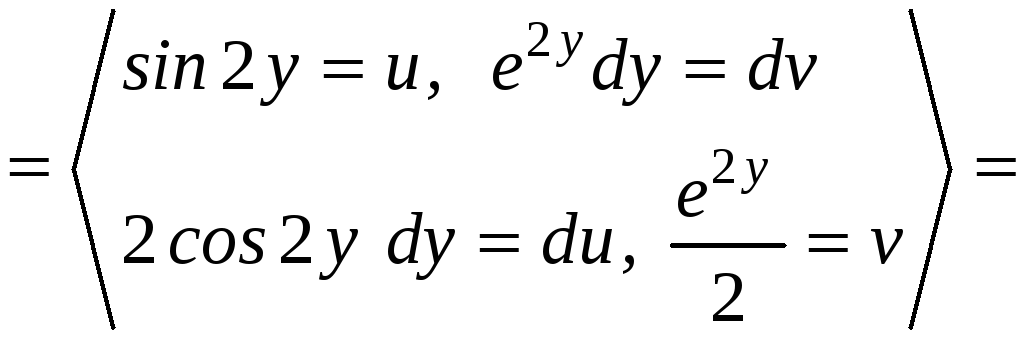
 ,
откуда
,
откуда
 .
.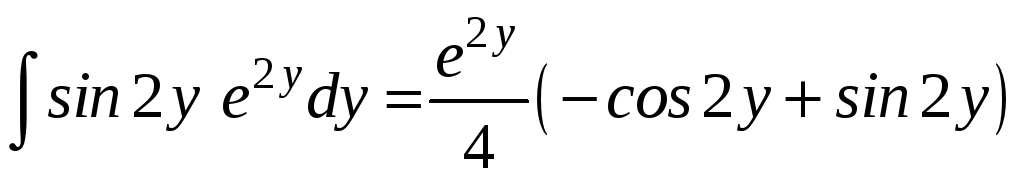 .
. .
. .
.
 ,
,
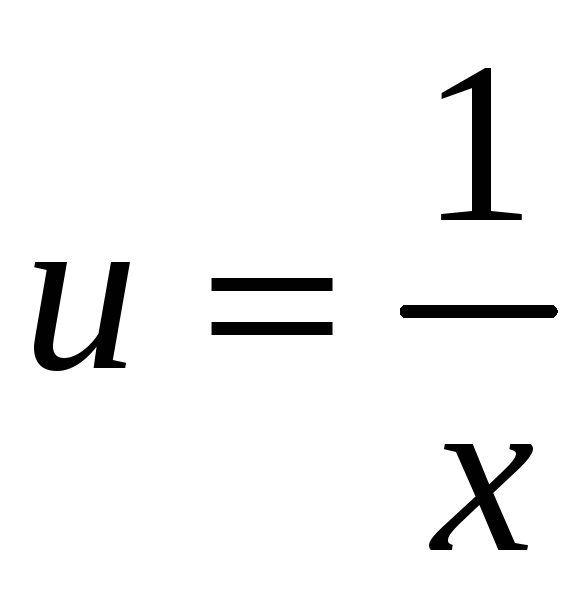 ,
,
 в уравнение, первое слагаемое обращается
в ноль, получаем уравнение с разделяющимися
переменными для
в уравнение, первое слагаемое обращается
в ноль, получаем уравнение с разделяющимися
переменными для
 . (2)
. (2)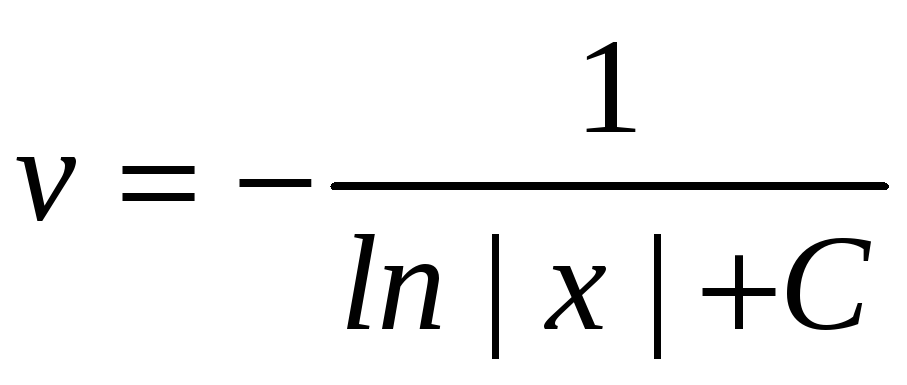 .
. . (3)
. (3)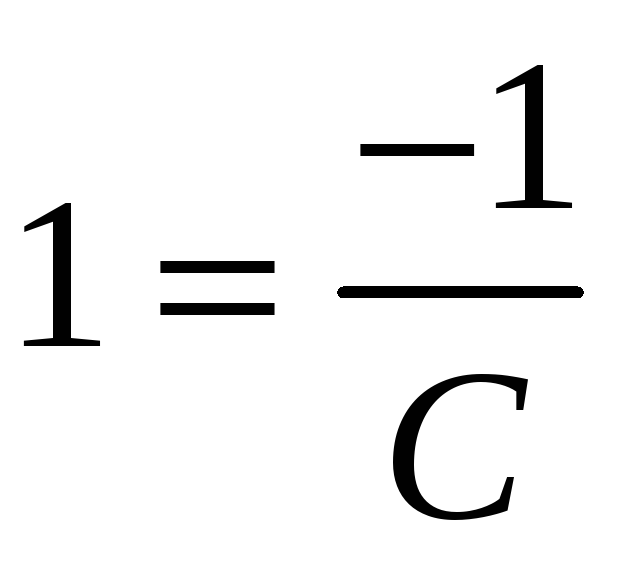 ,
,
 - единственное решение задачи.
- единственное решение задачи.
 .
. ,
,
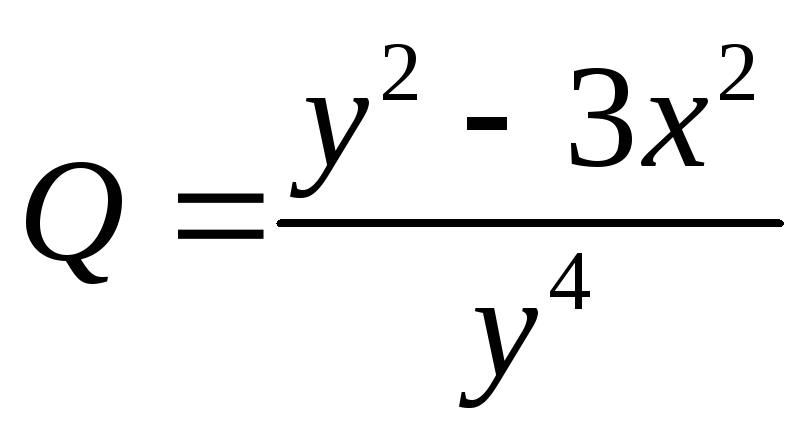 .
. ,
,
 ,
,
 ,
,
 .
. ,
,

 ,
,
 .
. ,
,
 ,
,
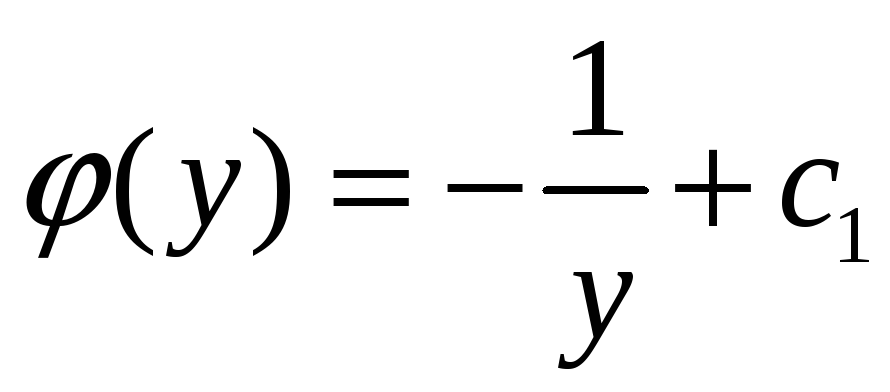 ,
,
 .
. .
. ,
,
 .
. ,
, .
.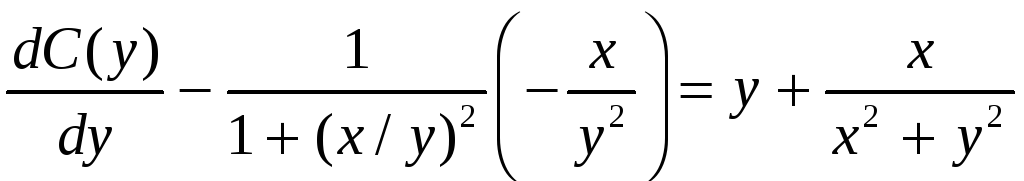
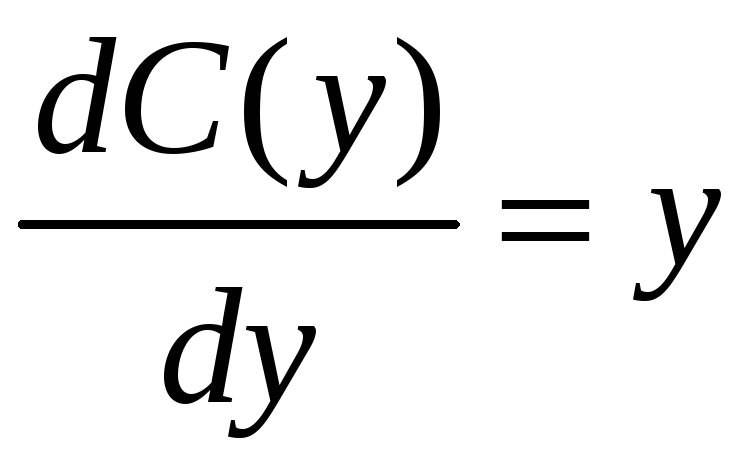 .
. .
. .
. .
. ,
,
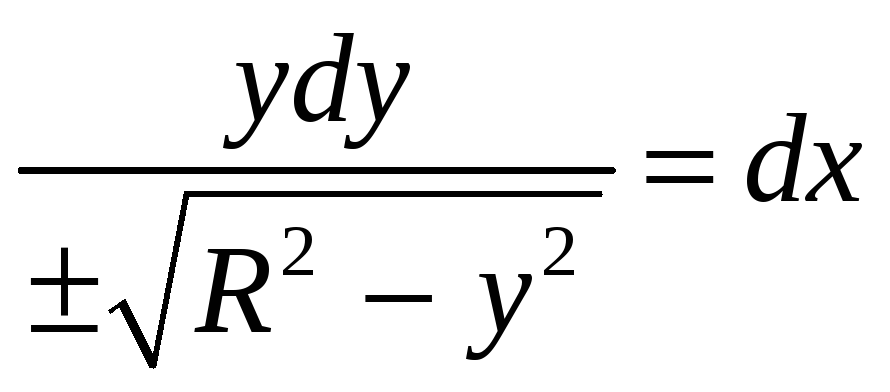 ,
,
 .
.

 .
. ,
,
