4. Интегрирование «по частям»

Идея этого метода основана на формуле производной произведения двух функций: [1] ─ применяется чаще всего тогда, когда подынтегральная функция может быть представлена в виде произведения пары хотя бы одной из следующих функций:и их вариаций.

Итак, если подынтегральную функцию можно представить в виде произведения, то сочетаниеилиможно принять за дифференциалили. Тогда решение интеграла получается по формуле.

Выбор функций-сомножителей определяется опытом самого решающего. Попытаемся показать это на конкретном примере.

Пример 7. .

Рецепт. Альтернатива выбора функций-сомножителей здесь небогатая: либо и, либо. Попробуем пойти первым путём

Вариант 1. . Повторно применяем этот же метод:и т.д. Очевидно, что этот путь ─тупиковый: с каждым новым шагом показатель степени при аргументе растёт и не видно конца этим манипуляциям. Очевидна и причина такого тупика ─ неудачный первоначальный выбор функции .

Не следует думать, что есть люди, которые ни разу не совершали подобную ошибку, просто из этого надо сделать позитивный вывод: «на ошибках учатся».

А теперь пойдём альтернативным путём:

Вариант 2: . Тогда.

Интересной особенностью данного метода является решение «рекурсивных интегралов». Рассмотрим один из вариантов таких интегралов.

Пример 8. .

Рецепт. Применим метод «по частям»: .

Сопоставив начало и конец этой цепочки, получаем решение .

5. Рациональные дроби

Известно [1], что дробь может называться «рациональной», если её числитель и знаменатель ─ целые числа. С этой точки зрения излагаемый дальше метод относится к интегралам вида , где, а─ полиномы порядкаисоответственно.

С точки зрения соотношения порядков полиномов возможны два варианта:

1. . В этом случае полином числителя «столбиком» делят на полином знаменателя, выделяя тем самым «целую» часть подынтегральной дроби и её «остаток». Тогда исходный интеграл можно представить в виде суммы двух интегралов: 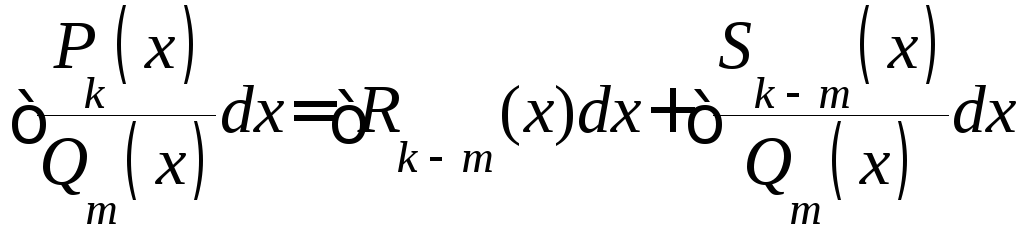, где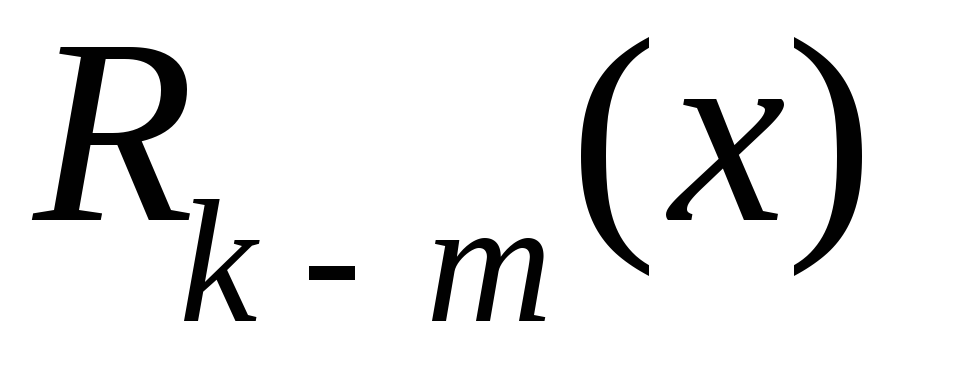

и ─ полиномы соответствующего порядка того же типа, что и исходные полиномы. Первый интеграл – сумма табличных интегралов. Ко второму интегралу применяют обычно метод «неопределённых коэффициентов», суть которого излагается дальше;

2. . Здесь сразу берётся интеграл указанным выше методом.

Метод «неопределённых коэффициентов»

Известно [1], что любой полином ^го порядка (n≥2) можно представить в виде произведения:

• (коэффициента при старшей степени полинома);

• двучленов типа ;

• трёхчленов типа

где ─ действительные числа (причём),действительный корень полиномаи─ кратности соответствующих сомножителей при условии, что. По отношению к полиному знаменателяэто означает, что подынтегральную функцию можно представить в виде суммы дробей типаи(и─ некие числовые коэффициенты) с соответствующими кратностями (повторами корней). Тогда нахождение интеграла от рациональной дроби сведётся к взятию табличного интеграла типаи интеграла типа, способ решения которого для=1 рассмотрен в Примере 2. Остаётся только освоить методику разложения рациональной дроби на соответствующие слагаемые.

Рассмотрим несколько примеров на эту тему.

Пример 9. .

Рецепт. Здесь порядок полинома числителя больше порядка полинома знаменателя, поэтому делим «столбиком» числитель на знаменатель:

Таким образом, , где = =. Здесьдействительные числа, которые подбираются следующим образом:

• сложим дроби: ;

• затем приравняем коэффициенты при соответствующих степенях аргумента и получим систему двух линейных уравнений для и:;

тогда решение этой системы:

Отсюда интеграл .

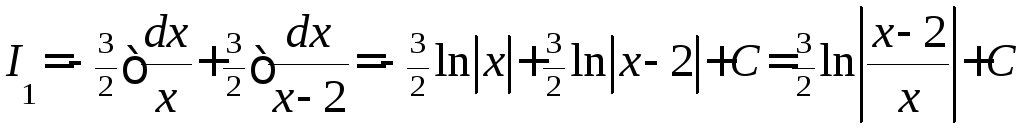Таким образом, общее решение можно представить в следующем виде .

Пример 10. .

Рецепт

1. Здесь порядок полинома числителя меньше порядка полинома знаменателя, поэтому не нужно выделять целую часть.

2. В предположении, что данный интеграл можно решить методом неопределённых коэффициентов, попробуем разложить полином знаменателя на множители.

Согласно теореме Виета, свободный член любого полинома равен произведению всех его корней на множитель , где– порядок полинома. Здесь, тогда этот множитель равен единице. Попробуем подобрать хотя бы один целый корень, возьмём, например,. Призначение полинома: 1-2+4-6+3=0, т.е.– один из корней. Теперь поделим исходный полином «столбиком» (см. выше) на двучлени получим полином третьего порядка. Сгруппируем соответствующие слагаемые:. Таким образом, подынтегральная функция должна иметь вид. В знаменателе имеется двучленкратности 2 и «усечённый» трёхчленс отрицательным дискриминантом. В этом случае подынтегральную функцию можно представить в виде суммы дробей: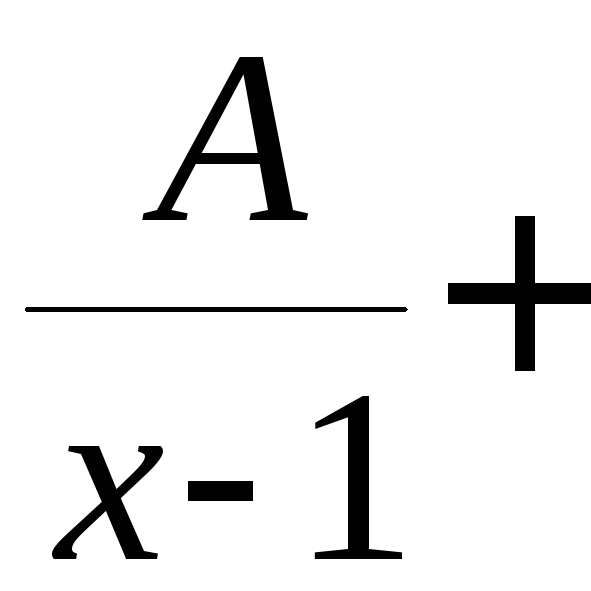

(здесь, как и раньше коэффициенты ─ действительные числа).

Обратите, пожалуйста, внимание на тот факт, что порядок полиномов в числителях этих дробей ровно на единицу меньше порядка полиномов в знаменателях!

В результате сложения этих дробей получаем дробь , числитель которой должен в точности совпадать с числителем дроби исходной подынтегральной функции. Это позволяет сформировать систему теперь ужечетырёх линейных уравнений для этих коэффициентов: .

Нетрудно показать, что решение этой системы и исходный интеграл равен сумме трёх интегралов:. Первые два – табличные, и их результат:. Решение последнего интеграла. Итак, ответ:

.

Обратите внимание на то, что громоздкий интеграл был сведён к комбинации табличных интегралов (решение последнего интеграла – см. Пример 3).

Пример 11. .

Рецепт. Покажем, что этот интеграл можно достаточно просто решить тем же методом «неопределённых коэффициентов». Для этого домножим числитель и знаменатель на . Подынтегральная функция примет вид. Опытный взгляд сразу увидит в числителе дифференциал функции. Отсюда возникает желание ввести замену:. Далее подставляем эти выражения в подынтегральную функцию, и интеграл приобретает следующий вид:─ и готов к приложению к нему метода «неопределённых коэффициентов»:. Знакомым уже способом получаем систему уравнений:. Из решения системы следует:и. После обратной подстановкиполучаем окончательный результат:.

Это очень полезный результат, поэтому есть смысл записать его в дополнительную таблицу неопределённых интегралов (см. табл.2).

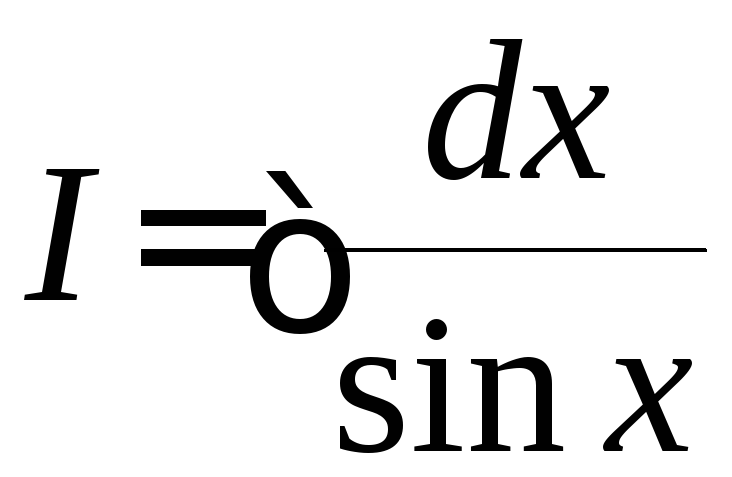Легко показать, что аналогичный интеграл =. С учётом формулиполучаем ещё один вариант решения этого интеграла:=+С. И этот результат рекомендуем внести в ту же дополнительную таблицу.

N.B. Несколько позже мы рассмотрим решение этого же интеграла другим способом.