Вариант № 9

1. Завышенное значение интеграла будет получено методом ……………прямоугольников.

2. Напишите формулу для вычисления второй производной «в центре». ___________________________________________________________

3. Необходимо сделать не менее …………. итераций, чтобы найти корень уравнения с точностьюметодом бисекции на отрезке[0; 1].

4. Чтобы построить полином Лагранжа 6-ой степени необходимо ………узлов интерполяции.

5. При уточнении корня уравнения на отрезке [a;b] методом хорд в качестве начального приближения следует взятьb, если………..

6. Почему итерационные методы являются самоисправляющимися? ___________________________________________________________

7. Запишите условие прекращения итераций для нахождения корня уравнения с точностью .

8. При каких значениях условием прекращения итераций для нахождения корня с точностьюможно считать условие?______________________________________________

9. Докажите, что если определить функцию по формул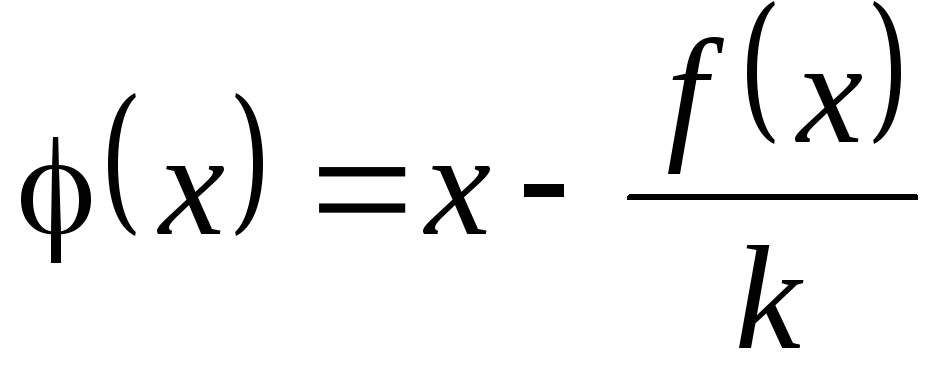е, где, а знак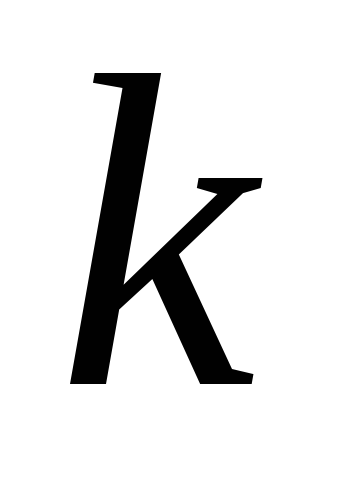совпадает со знакомна отрезке [a;b], то уравнениеэквивалентно уравнению, а функцияудовлетворяет достаточному условию сходимости. ________________________________________ _________________________________________________________________________________________________________________________________________________________________________________

10. Скорость сходимости метода Зейделя выше, чем метода простых итераций, когда выполняется условие сходимости:

    1. 

    2. 

    3. 

11. Напишите формулу для оценки погрешности численного дифференцирования «назад». _________________________________

12. Погрешность численного дифференцирования по «центральной» формуле оценивается из неравенства:

    1. 

    2. 

    3. 

13. Если значения функции y (x) рассчитываются с погрешностью, то оптимальный шаг численного дифференцирования по «центральной» формуле следует определять из соотношения:

    1. 

    2. 

    3. 

14. Какие ограничения накладываются на распределение узлов интерполяции по отрезку интерполирования при построении полинома Лагранжа? ________________________________________

15. Расчет интеграла методом ……………… прямоугольников даст завышенное значение.

16. При расчете интеграла по формуле Симпсона подынтегральная функция на отрезке длиной аппроксимируется полиномом ……..-ой степени.

17. Погрешность метода «средних» прямоугольников оценивается из неравенства:

    1. 

    2. 

    3. 

18. Напишите неравенство для оценки погрешности метода трапеций. ___________________________________________________________

19. Погрешность по методу Рунге для квадратурной формулы Симпсона оценивается из приближенного равенства:

    1. 

    2. 

    3. 

    4. 

20. Квадратурная формула Чебышева с nузлами дает точный результат для полинома степени …...

Вариант № 10

1. Напишите достаточное условие сходимости метода итераций для метрики ________________________________

2. Скорость сходимости метода Зейделя выше, чем метода простых итераций, когда выполняется условие сходимости:

1. 

2. 

3. 

3. Какой из концов отрезка [a;b] следует выбрать в качестве начального приближения в методе Ньютона, если, и? __________________________________________________

4. Выведите формулу для оценки погрешности численного дифференцирования «вперед». ________________________________ ___________________________________________________________

5. Погрешность численного дифференцирования по «центральной» формуле оценивается из неравенства:

1. 

2. 

3. 

6. Если значения функции y (x) рассчитываются с погрешностью, то оптимальный шаг численного дифференцирования по «центральной» формуле следует определять из соотношения:

1. 

2. 

3. 

7. Какие ограничения накладываются на распределение узлов интерполяции по отрезку интерполирования при построении полинома Лагранжа? ________________________________________

8. Необходимо определить производную …….-го порядка от функции f (x), чтобы оценить погрешность интерполяции этой функции полиномом Лагранжа 5-ой степени.

9. Как изменится оптимальный шаг численного дифференцирования по «центральной» формуле, если погрешность , с которой рассчитываются значения функцииy (x), уменьшится втрое? ______ ___________________________________________________________

10. Расчет интеграла методом ……………… прямоугольников даст завышенное значение.

11. При расчете интеграла по формуле Симпсона подынтегральная функция на отрезке длиной 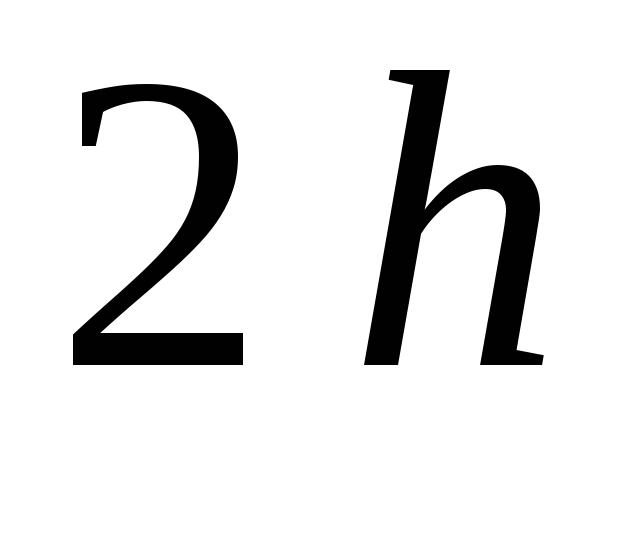аппроксимируется полиномом ……..-ой степени.

12. Погрешность метода «средних» прямоугольников оценивается из неравенства:

1. 

2. 

3. 

13. Погрешность по методу Рунге для квадратурной формулы Симпсона оценивается из приближенного равенства:

1. 

2. 

3. 

4. 

14. Квадратурная формула Чебышева с nузлами дает точный результат для полинома степени ….. .

15. Квадратурная формула Гаусса с nузлами дает точный результат для полинома степени ….. .

16. Если вторая производная подынтегральной функции f (x) неизвестна, то погрешность численного интегрирования методом трапеций можно оценить по формуле (приведите формулу): ___________________________________________________________

17. Система уравнений называется плохо обусловленной, если ………

18. Покажите, что метод хорд можно применить для нахождения корня уравнения на отрезке [0,5; 2]. _________________________ ______________________________________________________________________________________________________________________

19. В каких случаях метод Ньютона не определен? __________________

20. Необходимо найти корень уравнения на отрезке [0,2; 0,5] методом итераций. Можно ли выразить функциюкак? (Ответ обосновать.) ___________________________ ______________________________________________________________________________________________________________________

Учебное электронное текстовое издание

Чернышев Владимир Артурович

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

Редактор

Подготовка к публикации

Рекомендовано Методическим советом

Разрешено к публикации

Электронный формат– pdf

Объем уч.-изд.л.