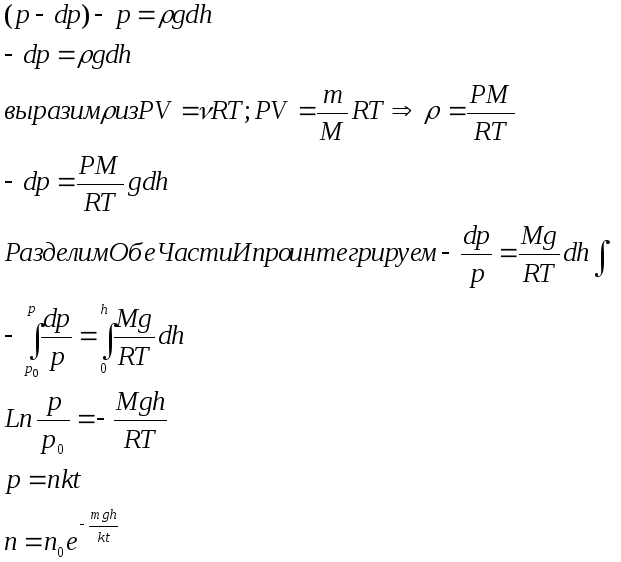Ответы на билеты…

1) Распределение Максвелла и его свойства (нахождение наиболее вероятной, средней арифметической и средней квадратической скоростей, зависимость функции распределения от температуры, от массы молекулы)

-Функция распределения молекул по модулю скорости, ил функция распределения Максвелла 1859г. В основе физической статистики Максвелла(сер 19 века) лежат принципы: 1)все частицы различимы и их можно пронумеровать. 2)физические характеристики частиц могут принимать любые значения (V,p,W). ОдинаковымWиpмогут обладать бесконечно много частиц.

где m-масса одной молекулы [КГ]; k-постоянная Больцмана -1,38*10^-23 [Дж/К]; T- температура [К].

Нахождение наиболее вероятной скорости:

Нахождение средней арифметической скорости:

Нахождение средней квадратичной скорости:

Зависимость функции распределения от температуры:

Зависимость функции распределения от массы молекулы:

2) Функция распределения по энергиям и относительным скоростям (вывод).

Вывод функции распределения по энергиям: функция распределения молекул идеального газа по кинетическим энергиям вводится аналогично функции распределения по модулю скоростиF(V): гдеdW_K-число молекул, кинетические энергии которых попадают в бесконечно малый интервал (W_K, W_K+dW_k), а dP(W_K)- Вероятность того, что кинетическая энергия молекулы в отдельном опыте попадает в бесконечно малый интервал (W_K, W_K+dW_k). Формула для функции F(W_K) можно получить из того условия, что число молекул, кинетические энергии которых попадают в интервал кинетических энергий (W_K, W_K+dW_k), равно числу молекул, скорости которых попадают в интервал скоростей (V, V+dV). Это является следствием формулы для кинетической энергии молекулы W_K=m₀V²/2. Итак

Заменяя в полученном выражении скорость V через кинетическую энергию молекулы (), для функции распределения молекул по их кинетическим энергиям получим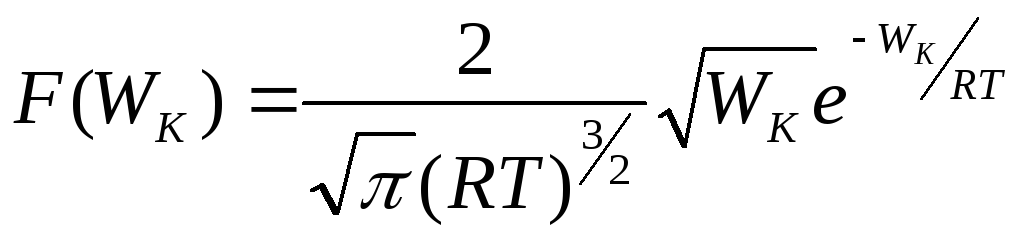

Таким же способом можно получить функции распределения молекул по относительным скоростям (U=V/V_a)

3) Распределение Больцмана (Вывод):

Пусть идеальный газ находится во внешнем поле, в котором потенциальная энергия молекулы равна W_p(x,y,z). Температура газа во всех точках пространства одинакова и равна T. В этом случае равновесное распределение частиц в пространстве устанавливается за счет двух факторов –теплового движения, которое стремится разбросать частицы идеального газа равномерно по всему пространству (энергия теплового движения определяется энергией RT), и сил потенциального поля, которые стремятся расположить частицы в тех точках пространства, где их потенциальная энергия минимальна. Больцман показал, что в этом случае функция распределения частиц идеального газа по координатам записывается:

Функция распределения Больцмана F(x,y,z) является плотностью вероятности, она равна отношению вероятности d P(x,y,z) найти частицу в бесконечно малом объеме dV, или отношению относительного числа частиц dN (x,y,z)/N попадающий в бесконечно малый объем dV около точки пространства с координатами (x,y,z), к величине объема dV. Функция распределения Больцмана F(x,y,z) позволяет найти вероятность P(V₁) попадания молекулы в произвольный объем V₁ пространства ли относительное число молекул N(V₁)/N, попадающих в этот объем V₁ около точки с координатами (x,y,z) , где интеграл берется по объему пространстваV₁. Входящая в эту формулу концентрация n₀ находим из условия нормировки . В этой формуле интеграл берется по всему объему, занимаемому газом. Предпоследнюю формулу можно упростить, еслиV₁ будет малым( в пределах объема V₁=∆V функция остается неизменной):

Барометрическая формула Больцмана: если применить формулу распределения Больцмана для идеального газа, находящегося в потенциальном поле тяготения Земли, учитывая что W_P(x,y,z)=m₀gh, n(x,y,z)=n(h) формулу можно переписать следующим образом,гдеn₀- концентрация газа на поверхности Земли. Запишем Барометрическую формулу, определяющую зависимость давления воздуха от высоты над поверхностью Земли:, гдеM-молярная масса газа, p₀- давление газа на поверхности Земли, с высотой изменятся: с повышением высоты –повышается концентрация газов с меньшей молярной массой. Вывод Барометрической формулы: давление газа на данной высоте h обусловлено давлением вышележащих слоев газа. Найдем давление dp, созданное слоем газа толщиной dh и площадью основания S на высоте h, давление на этой высоте обозначим p, тогда:

При выводе этой формулы было учтено, что с увеличением высоты давление газа падает то есть производная dp/dh меньше нуля.

Распределение Максвелла- Больцмана называют функцией распределения молекул по полной энергии частиц.

Рассмотрим идеальный газ. Будем считать , что T одинакова во всех точках поля. В этом случае равновесное распределение молекул достигается в результате 2-х факторов:1) силы потенциального поля пытаются распределить молекулы в положение их устойчивого равновесия; 2) тепловое движение молекулы равномерно по всему объему. ВЫВОД: совместное действие 2-х факторов приводит к такому распределению молекул что концентрация молекул убывает с ростом высоты: а) потенциальное поле Е_р; б)T-const; в)m- одинаковы.

Рассмотрим идеальный газ в бесконечно высоком цилиндре.

(p-dp)-p