Вариант 8

1. ABCDEF – правильный шестиугольник, причем =,=. Выразите черезивекторы,,,,,,.

2. Найдите угол, образованный единичными векторами 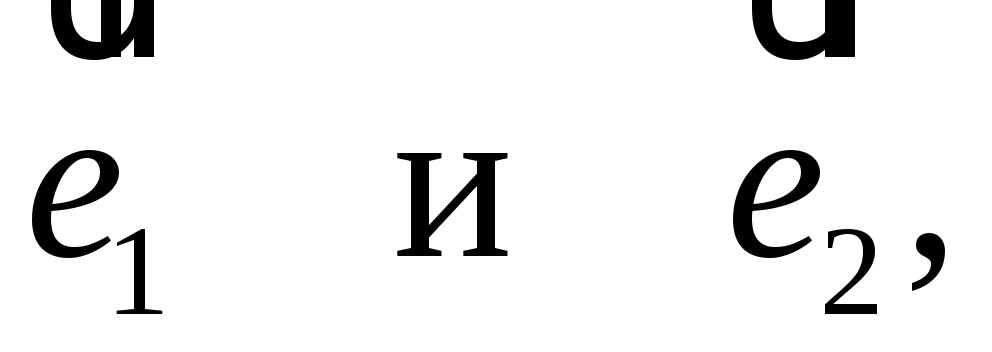если известно, что векторыперпендикулярны.

3. Найдите тупой угол (в радианах) между диагоналями параллелограмма, построенного на векторах .

4. Найдите уравнения и длины сторон треугольника, если заданы две его вершины А(-1, -1), В(-11, 4) и точка пересечения его высот К(-7, -4).

5. Постройте кривую

6. Приведите кривую к каноническому виду.

7. Найдите точку, симметричную точке относительно прямой

8. Составьте уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям

9. Докажите, что прямая пересекает ось абсцисс.

10. Составьте уравнения прямых, образованных пересечением плоскости с координатными плоскостями.

11. Составьте уравнение сферы, если известно, что точки (3;-3;2)и(5;3;-6) являются концами диаметра сферы.

12. Найдите уравнения линий пересечения поверхности с координатными плоскостями.

Вариант 9

1. В пространстве заданы треугольники ABC и .M и – точки пересечения их медиан. Выразите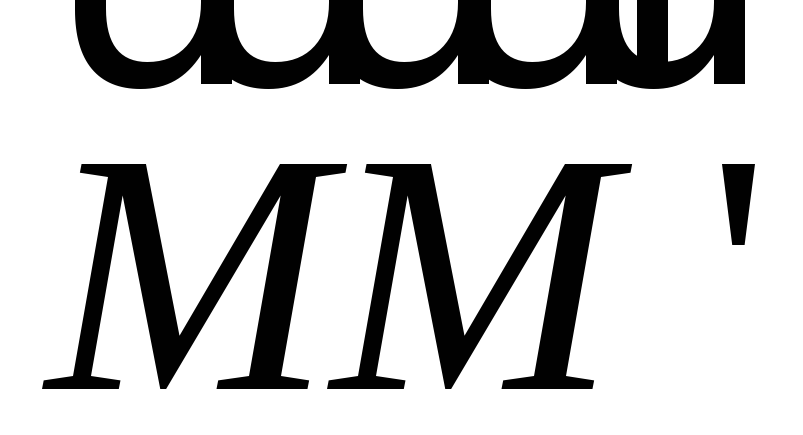через векторы,и.

2. Докажите, что вектор перпендикулярен вектору.

3. Найдите вектор 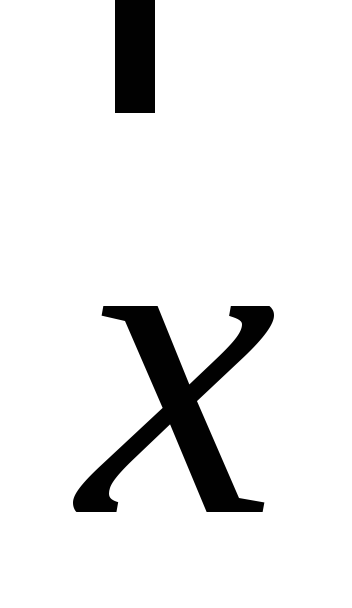, коллинеарный вектору, если его проекция на векторравна 5.

4. Найдите координаты вершин треугольника, если даны уравнения двух его сторон ,и двух его высот:,.

5. Постройте кривую

6. Приведите кривую к каноническому виду.

7. Найдите точку, симметричную точке 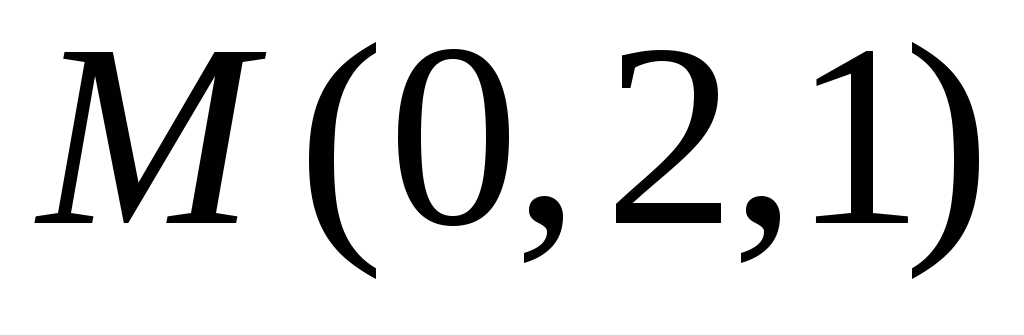относительно прямой

8. Составьте уравнение плоскости, которая проходит через точку перпендикулярно к двум плоскостям:

9. Составьте уравнение плоскости, проходящей через прямую перпендикулярно к плоскости

10. Проверьте параллельность прямых иили найдите угол между ними.

11. Составьте уравнение сферы, если известны координаты ее центра С (1;-4;-1) и то, что плоскость 2x – y + 2z + 2 = 0 касается сферы.

12. Найдите уравнения линий пересечения поверхности с координатными плоскостями.

Вариант 10

1. Точки E и F – середины сторон AD и BC четырехугольника ABCD.

Докажите, что =(+).

2. Для векторов вычислите проекцию векторана вектор.

3. Упростите выражение

4. Найдите уравнения и длины сторон и медиан треугольника,если даны две его вершины А (-1, 1), В(19, -9) и точка М (29/3; -1/3) пересечения медиан.

5. Постройте кривую .

6. Приведите кривую к каноническому виду.

7. Найдите точку, симметричную точке относительно прямой

8. Определите двугранный угол, образованный пересечением плоскостей

9. Вычислите кратчайшее расстояние между прямыми:

10. Составьте уравнения проекции прямой на плоскость.

11. Составьте уравнение сферы, если известно, что точки лежат на сфере.

12. Найдите уравнения линий пересечения поверхности с координатными плоскостями.

Вариант 11

1. Дан произвольный треугольник ABC. Докажите, что существует треугольник , стороны которого соответственно равны и параллельны медианам исходного треугольникаABC.

2. Для векторов вычислите проекцию вектора на вектор

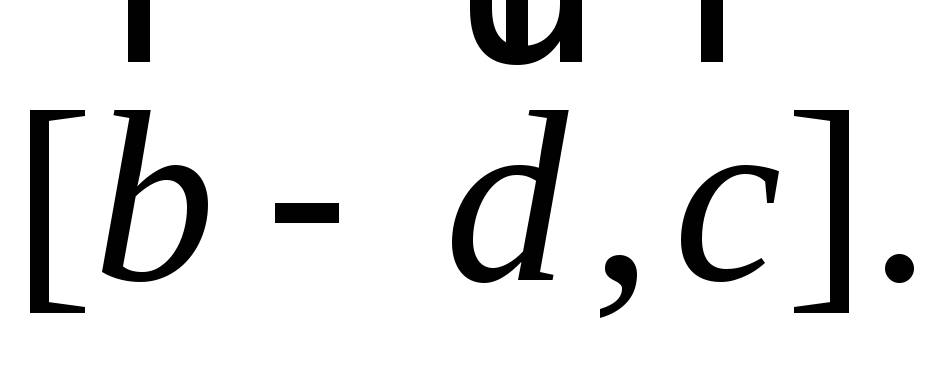
3. Проверьте, компланарны ли векторы .

4. Найдите уравнения и длины сторон и медиан треугольника, если заданы три его вершины А(1, -1), В(21, -11) и С(13, 5).

5. Постройте кривую .

6. Приведите кривую к каноническому виду.

7. Найдите точку, симметричную точке 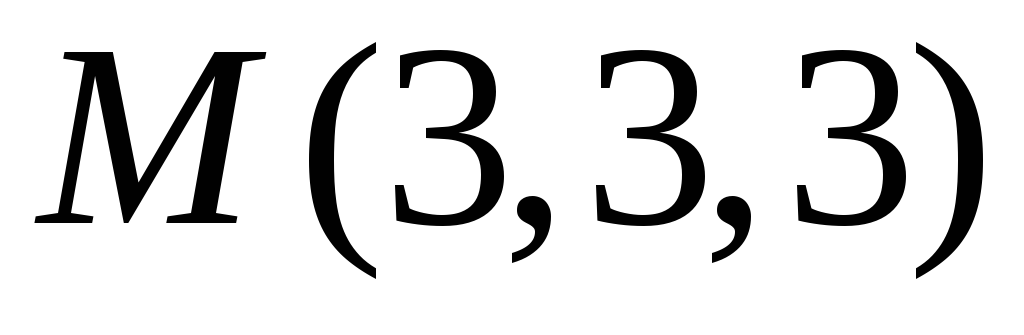относительно прямой

8. Точка служит основанием перпендикуляра, опущенного из начала координат на плоскость. Составьте уравнение этой плоскости.

9. Найдите координаты проекции точки М(0;2;1) на плоскость .

10. Докажите, что прямая лежит в плоскостиP:

11. Составьте уравнение сферы, если известны координаты ее центра C (0;-5;3) и радиус R = 5.

12. Найдите уравнения линий пересечения поверхности с координатными плоскостями.