Вариант 5

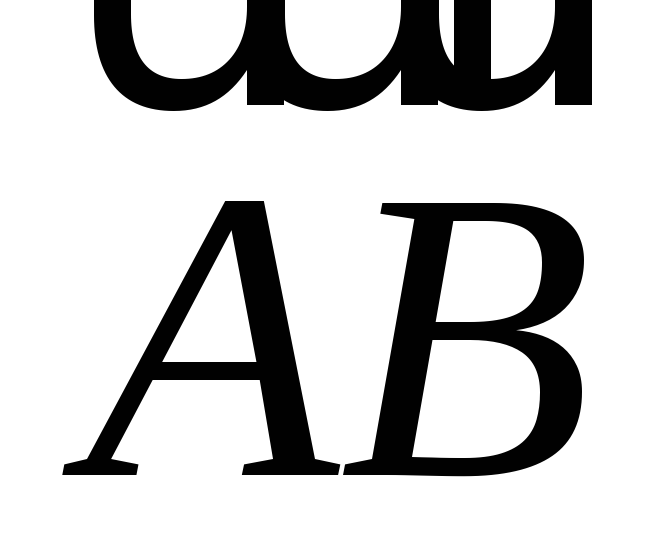1. Дан параллелепипед . Принимая за начало координат вершину, а за базисные векторы,,, найдите координаты: а) точекипересечения диагоналей гранейи; б) точки О пересечения диагоналей параллелепипеда.

2. Найдите направляющие косинусы вектора , если ,.

3. Найдите площадь параллелограмма, построенного на векторах и, еслии- единичные векторы и.

4. Найдите уравнения и длины сторон и медиан треугольника,если даны две его вершины А(-1, -1), В(9, -6) и точка пересечения его медиан М(13/3; -5/3).

5. Постройте кривую

6. Приведите кривую к каноническому виду.

7. Найдите точку, симметричную точке относительно прямой

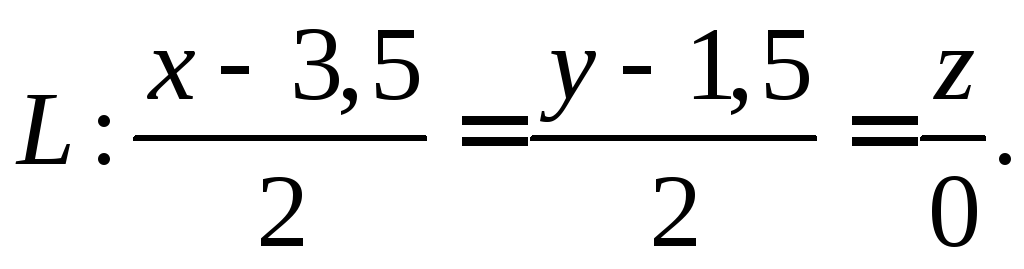
8. Определите двугранный угол, образованный пересечением пары плоскостей

9. Вычислите кратчайшее расстояние между прямыми: и.

10. Составьте уравнения проекции прямой на плоскость.

11. Составьте уравнение сферы, если известно, что точки ,,,лежат на сфере.

12. Найдите уравнения линий пересечения поверхности с координатными плоскостями.

Вариант 6

1. В трапеции ABCD известно отношение длин оснований: . Найдите координаты векторав базисе из векторови.

2. Заданы векторы . Найдите: а)б)с).

3. Даны три вектора Найдите координаты векторав базисе из векторови.

4. Найдите уравнения и длины сторон и медиан треугольника, если даны три его вершины А(1, 1), В(-9, 6), С(-5, -2).

5. Постройте кривую

6. Приведите кривую к каноническому виду.

7. Найдите точку, симметричную точке относительно прямой

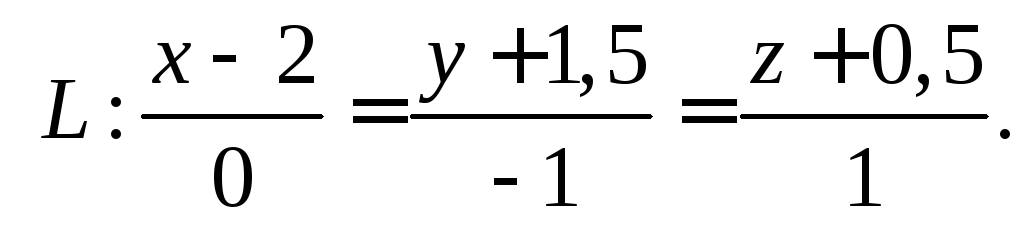
8. Точка служит основанием перпендикуляра, опущенного из начала координат на плоскость. Составьте уравнение этой плоскости.

9. Найдите координаты проекции точки М (1,0,1) на плоскость .

10. Докажите, что прямая лежит в плоскости

11. Составьте уравнение сферы, если известны координаты ее центра C (-3;-1;2) и радиус R = 3.

12. Найдите уравнения линий пересечения поверхности с координатными плоскостями.

Вариант 7

1. В тетраэдре ABCD DM – медиана грани BCD и Q – центр масс этой грани. Найдите координаты векторов и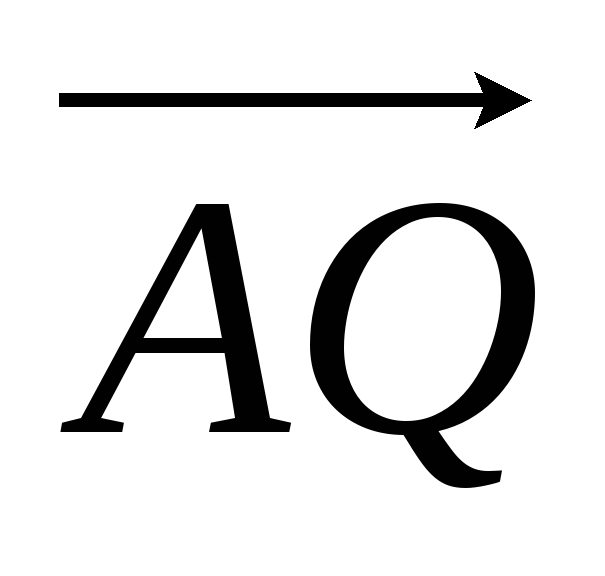в базисе,,.

2. Определите координаты точки М, если ее радиус-вектор составляет с координатными осями одинаковые углы, а его модуль равен 3.

3. Даны точки A(1, 2, 0), B(0, 1, 4) и С(-1, 1, 1). На плоскости XOZ найдите такую точку D, чтобы вектор был коллинеарен вектору.

4. Найдите вершины и уравнения медиан треугольника, если даны уравнения трех его сторон АС: х-2у-3=0; АВ: х+2у+1=0; ВС: 2х+у+14=0.

5. Постройте кривую

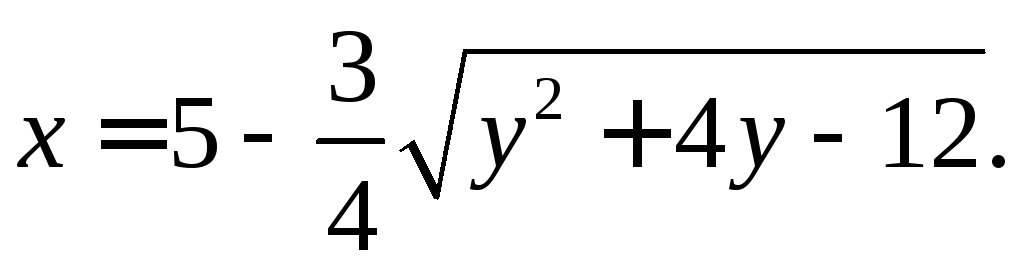
6. Приведите кривую к каноническому виду

7. Найдите точку, симметричную точке относительно прямой

8. Укажите значение λ, при котором плоскости : 3x – λy + 3 = 0 и :x – 2y + 5z – 10 = 0 будут перпендикулярны.

9. Составьте уравнения прямой, образованной пересечением плоскости Р: -5x + 2y – z + 1 = 0 с плоскостью, проходящей через ось аппликат и точку

10. Найдите точки пересечения прямой с координатными плоскостями.

11. Составьте уравнение сферы, если известны координаты ее центра C (-3;2;-1) и точки M(-2;1;-3) на ней.

12. Найдите уравнения линий пересечения поверхности с координатными плоскостями.