
- •Домашние задания Дз № 1. Векторная алгебра
- •Дз № 2. Прямая и плоскость
- •Дз №3. Прямая на плоскости
- •Дз № 4. Кривые на плоскости
- •Дз № 5. Поверхности в пространстве
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •8. Пример вариантов контрольных работ Векторная алгебра
- •Аналитическая геометрия
Дз № 5. Поверхности в пространстве
|
1 |
1.344 |
Установить,
какой геометрический образ определяется
уравнением
|
Плоскость
|
|
2 |
1.345 |
Установить,
какой геометрический образ определяется
уравнением
|
Плоскость
с нормальным вектором
|
|
3 |
1.346 |
Установить,
какой геометрический образ определяется
уравнением
|
Сфера радиуса R = 2 с центром в начале координат |
|
4 |
1.347 |
Установить,
какой геометрический образ определяется
уравнением
|
Сфера
радиуса R
= 4 с центром
в точке
|
|
5 |
1.348 |
Установить,
какой геометрический образ определяется
уравнением
|
Начало координат |
|
6 |
1.349 |
Установить,
какой геометрический образ определяется
уравнением
|
Ось Оу |
|
7 |
1.350 |
Установить,
какой геометрический образ определяется
уравнением
|
Пустое множество |
|
8 |
1.351 |
Установить,
какой геометрический образ определяется
уравнением
|
Пара
пересекающихся плоскостей
|
|
9 |
1.352 |
Установить,
какой геометрический образ определяется
уравнением
|
Пара координатных плоскостей Оуz и Oxy |
|
10 |
1.353 |
Установить,
какой геометрический образ определяется
уравнением
|
Тройка координатных плоскостей |
|
11 |
1.354 |
Установить,
какой геометрический образ определяется
уравнением
|
Пара
плоскостей
|
|
12 |
1.355 |
Установить,
какой геометрический образ определяется
уравнением
|
Пара
плоскостей
|
|
13 |
1.361 а,в,г,д |
Составить
уравнение сферы в каждом из следующих
случаев (обозначено:
С
– центр сферы, R
– радиус,
|
а)
в)
г)
д) |
|
14 |
1.372 |
Установить
тип поверхности
|
Эллипсоид |
|
15 |
1.373 |
Установить
тип поверхности
|
Однополостный гиперболоид |
|
16 |
1.374 |
Установить
тип поверхности
|
Двуполостный гиперболоид вращения |
|
17 |
1.375 |
Установить
тип поверхности
|
Конус |
|
18 |
1.376 |
Установить
тип поверхности
|
Параболоид вращения |
|
19 |
1.377 |
Установить
тип поверхности
|
Гиперболический параболоид |
|
20 |
1.378 |
Установить
тип поверхности
|
Эллиптический параболоид |
|
21 |
1.379 |
Установить
тип поверхности
|
Параболический цилиндр |
|
22 |
1.380 |
Установить
тип поверхности
|
Параболоид вращения с вершиной (0,0,2) |
|
23 |
1.381 |
Установить
тип поверхности
|
Гиперболический параболоид |
|
24 |
1.382 |
Установить
тип поверхности
|
Однополостный гиперболоид вращения |
|
25 |
1.383 |
Установить
тип поверхности
|
Двуполостный гиперболоид вращения |
|
26 |
1.393 |
Построить
цилиндрическую поверхность
|
|
|
27 |
1.394 |
Построить
цилиндрическую поверхность
|
|
|
28 |
1.395 |
Построить
цилиндрическую поверхность
|
|
|
29 |
1.396 |
Построить
цилиндрическую поверхность
|
|
|
30 |
1.397 |
Построить
цилиндрическую поверхность
|
|
|
31 |
1.398 |
Построить
цилиндрическую поверхность
|
|
|
32 |
1.399 |
Построить
цилиндрическую поверхность
|
|
|
33 |
1.400 |
Построить
цилиндрическую поверхность
|
|
|
34 |
1.401 |
Построить
цилиндрическую поверхность
|
|
|
35 |
1.402 |
Построить
цилиндрическую поверхность
|
|
Министерство образования и науки Российской Федерации Уральский федеральный университет имени первого Президента России Б.Н. Ельцина
Кафедра высшей математики
РАСЧЕТНАЯ РАБОТА № 2
Векторная алгебра и аналитическая геометрия
Студент
Группа
Преподаватель
Вариант
Дата
Екатеринбург 2010

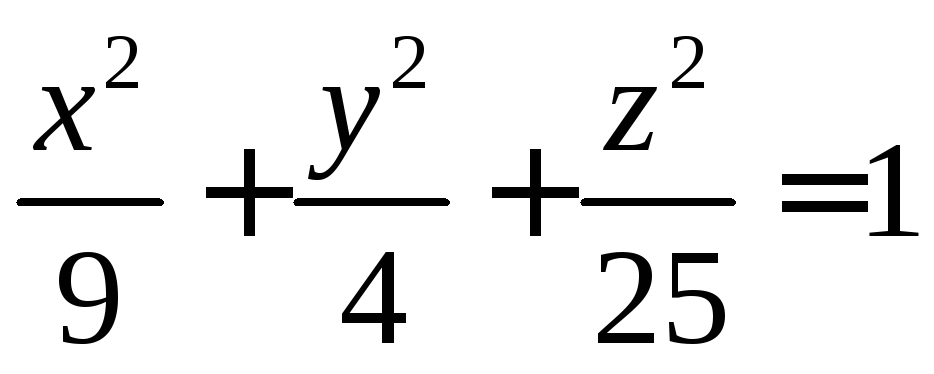 и построить ее.
и построить ее. и построить ее.
и построить ее. и построить ее.
и построить ее. .
.