
- •Домашние задания Дз № 1. Векторная алгебра
- •Дз № 2. Прямая и плоскость
- •Дз №3. Прямая на плоскости
- •Дз № 4. Кривые на плоскости
- •Дз № 5. Поверхности в пространстве
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •8. Пример вариантов контрольных работ Векторная алгебра
- •Аналитическая геометрия
Вариант 22
В плоскости треугольника АВС найдите точку О такую, что
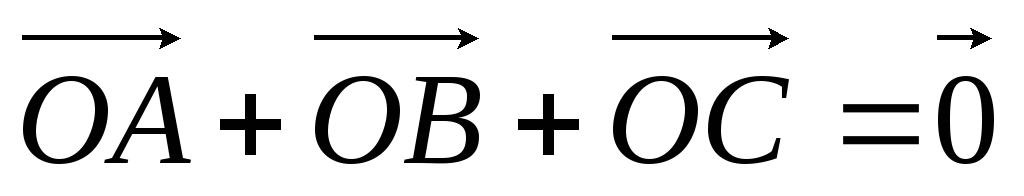 .
Существуют ли такие точки вне плоскости
треугольника?
.
Существуют ли такие точки вне плоскости
треугольника?Векторы
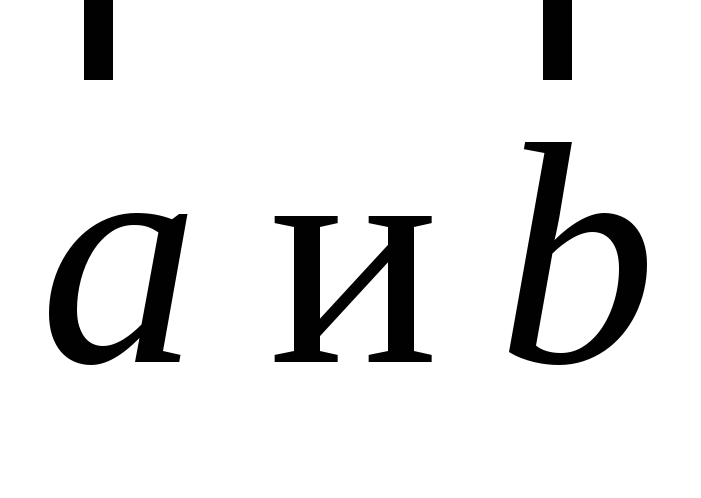 неколлинеарны. При каких значениях
скалярной величины
векторы
неколлинеарны. При каких значениях
скалярной величины
векторы
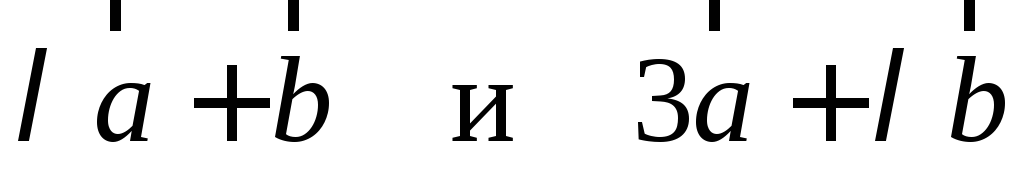 коллинеарны?
коллинеарны?Образуют ли базис в пространстве векторы {1; 0; 0},
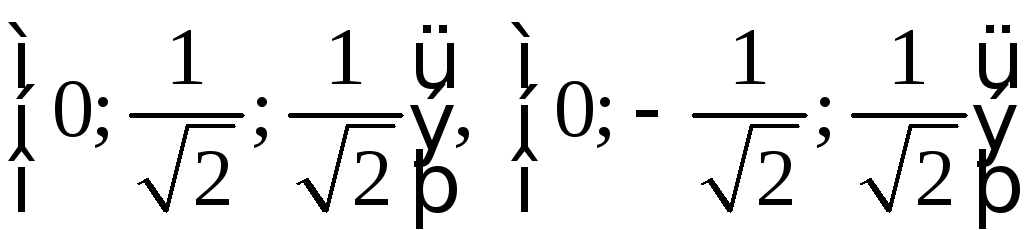 ?
Будет ли он ортонормированным?
?
Будет ли он ортонормированным?Найдите вершины и уравнения медиан треугольника, если даны уравнения трех его сторон
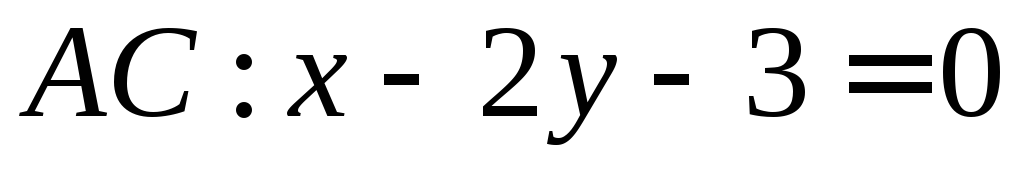 ;
;
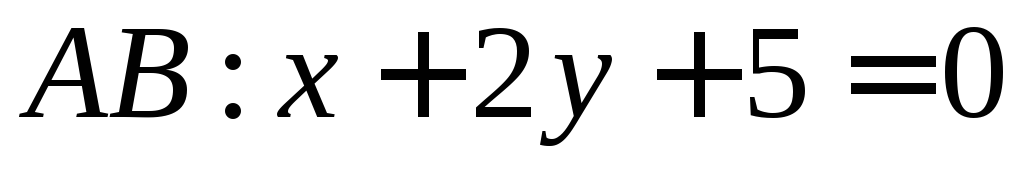 ;
;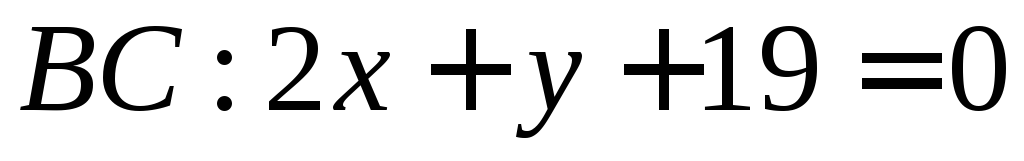 .
.Постройте кривую
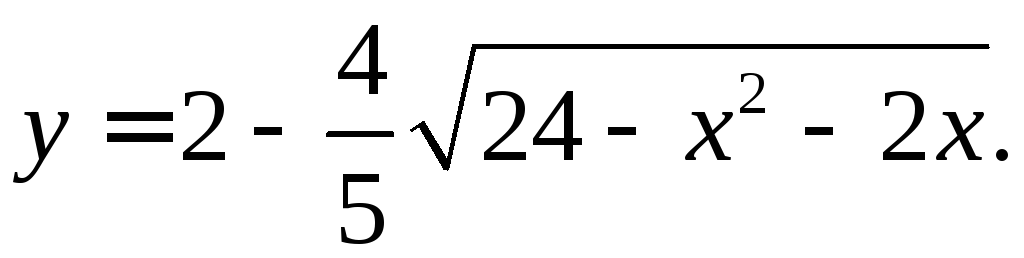
Приведите кривую
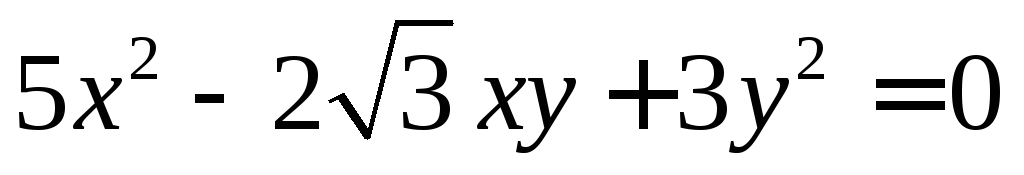 к каноническому виду.
к каноническому виду.Найдите точку, симметричную точке
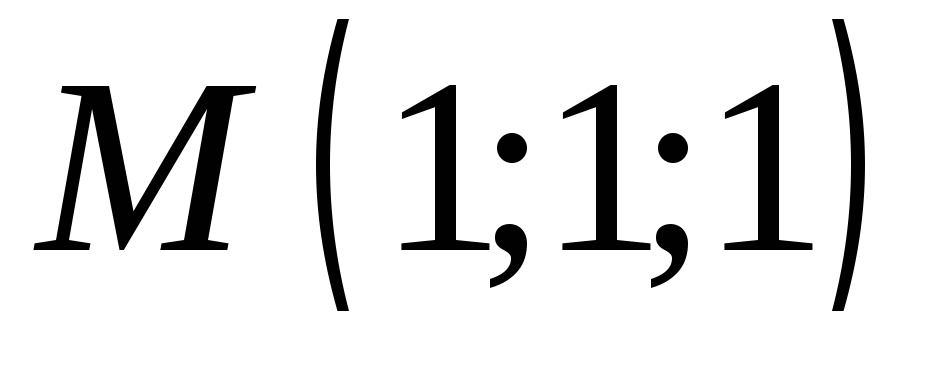 относительно плоскости
относительно плоскости
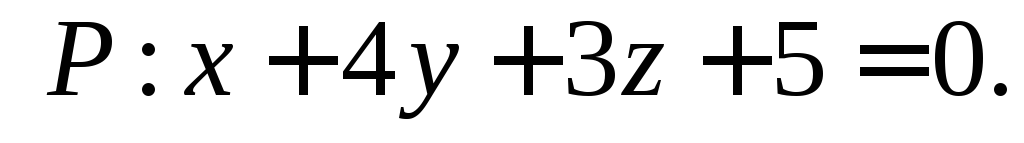
Укажите значение λ, при котором плоскости
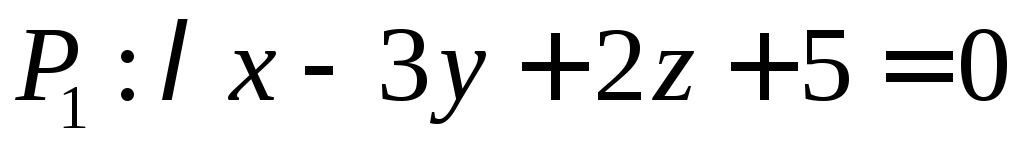 и
и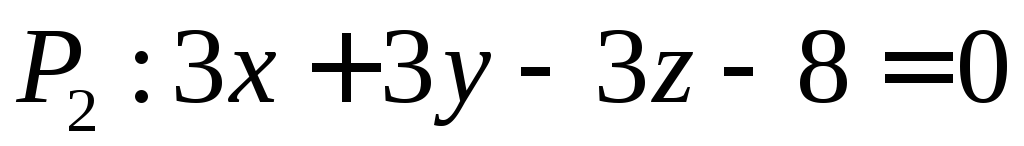 будут перпендикулярны.
будут перпендикулярны.Составьте уравнения прямой, образованной пересечением плоскости
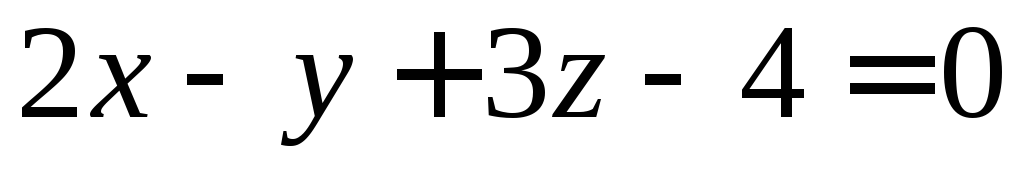 с плоскостью, проходящей через ось
абсцисс и точку
с плоскостью, проходящей через ось
абсцисс и точку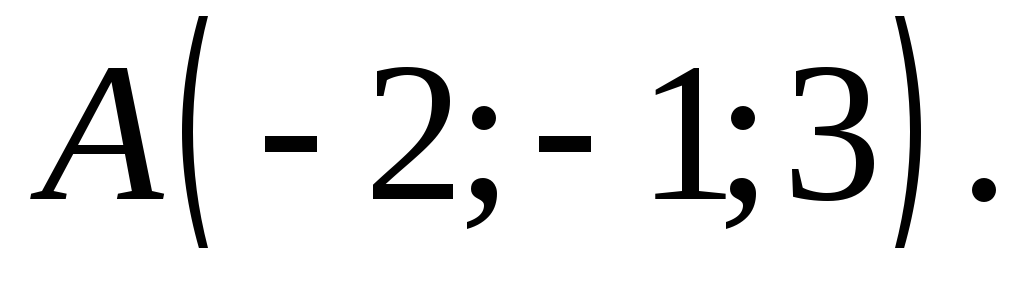
Найдите точки пересечения прямой
 с координатными плоскостями.
с координатными плоскостями.Составьте уравнение сферы, если известны координаты ее центра C (2;-1;3) и точки M (0;1;2) на сфере.
Найдите уравнения линий пересечения поверхности
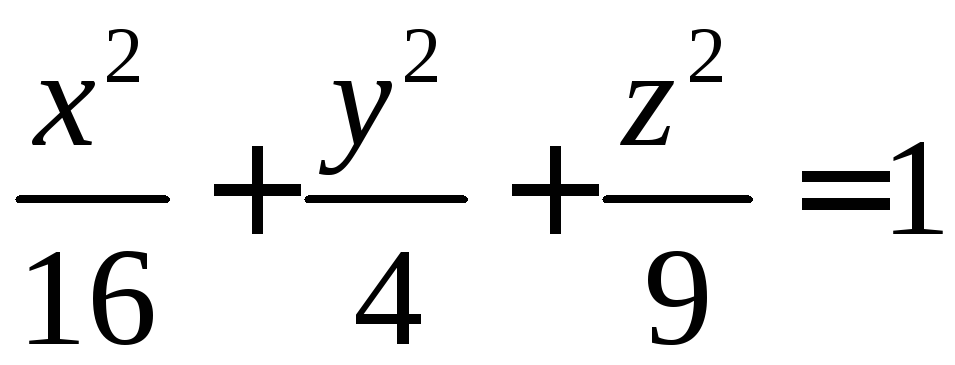 с координатными плоскостями.
с координатными плоскостями.
Вариант 23
Даны 3 точки
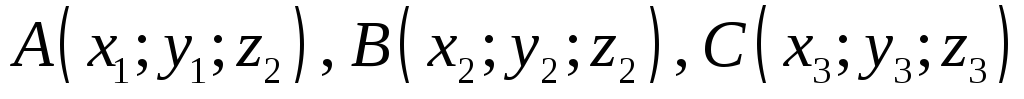 ,
не лежащие на одной прямой. Найдите
координаты точки пересечения медиан
треугольникаАВС.
,
не лежащие на одной прямой. Найдите
координаты точки пересечения медиан
треугольникаАВС.Найдите направляющие косинусы вектора
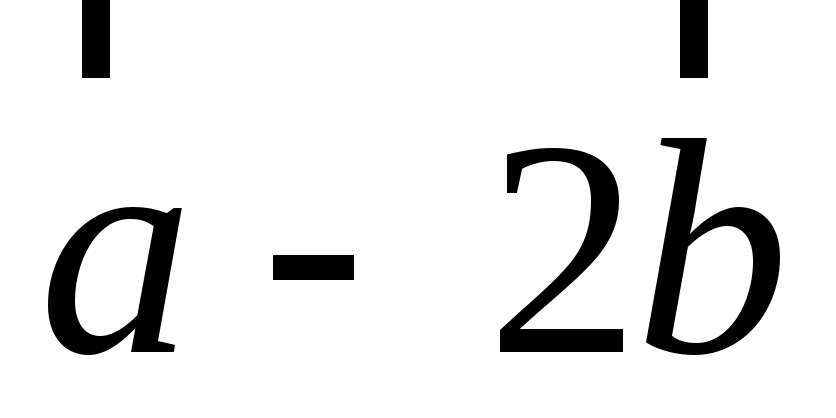 ,
если
,
если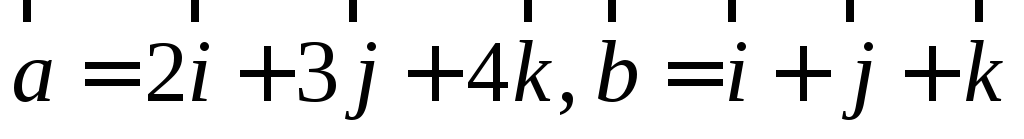 .
.Вычислите: 1)
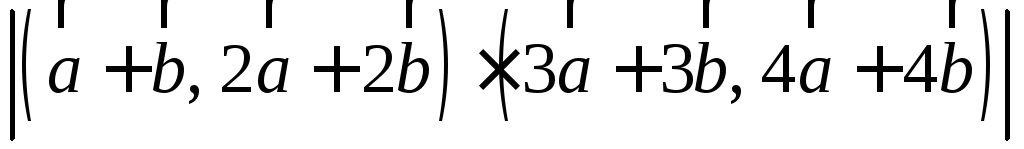 ;
2)
;
2)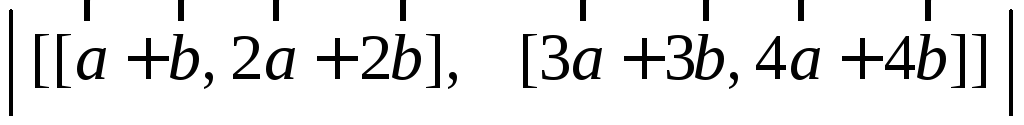 .
.Найдите уравнения и длины сторон треугольника, если даны две его вершины А(1; 2), В(21; -8) и точка К(13; 8) пересечения его высот.
Постройте кривую

Приведите кривую
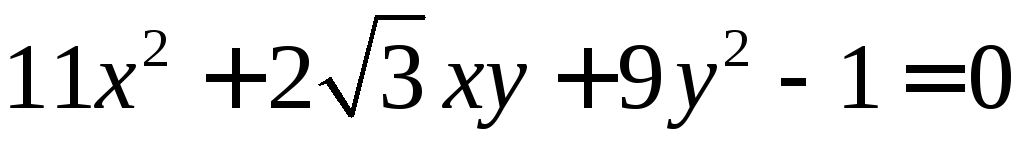 к каноническому виду.
к каноническому виду.Найдите точку, симметричную точке
 относительно плоскости
относительно плоскости
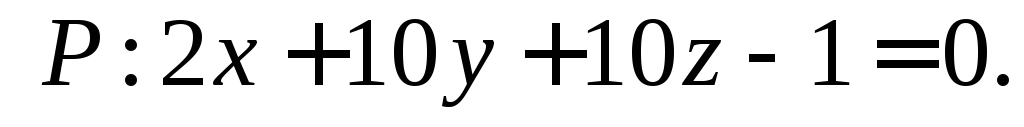
Составьте уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям
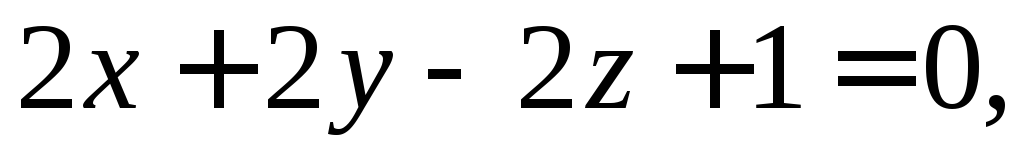

Докажите, что прямая
 пересекает ось ординат.
пересекает ось ординат.Составьте уравнения прямых, образованных пересечением плоскости
 с координатными плоскостями.
с координатными плоскостями.Составьте уравнение сферы, если известно, что точки
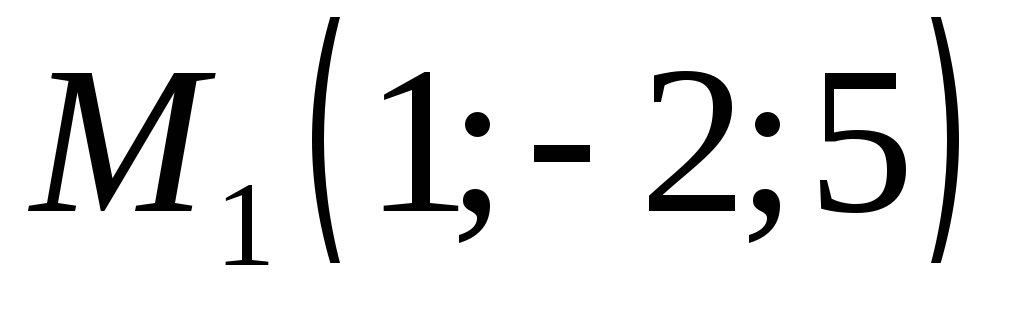 и
и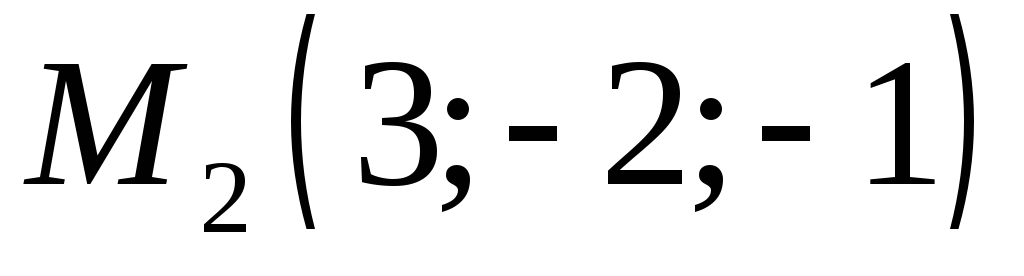 - концы ее диаметра.
- концы ее диаметра.Найти уравнения линий пересечения поверхности
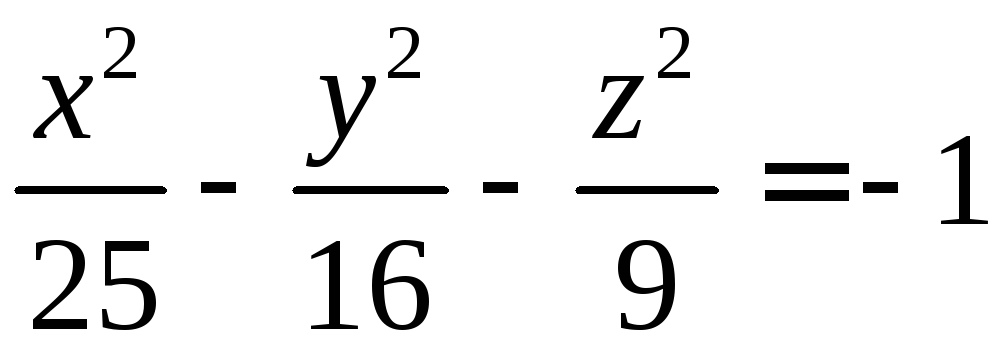 с координатными плоскостями.
с координатными плоскостями.
Вариант 24
В трапеции ABCD длины оснований AD и BC относятся как 4 : 1. Принимая за начало координат вершину А, а за базисные векторы
 и
и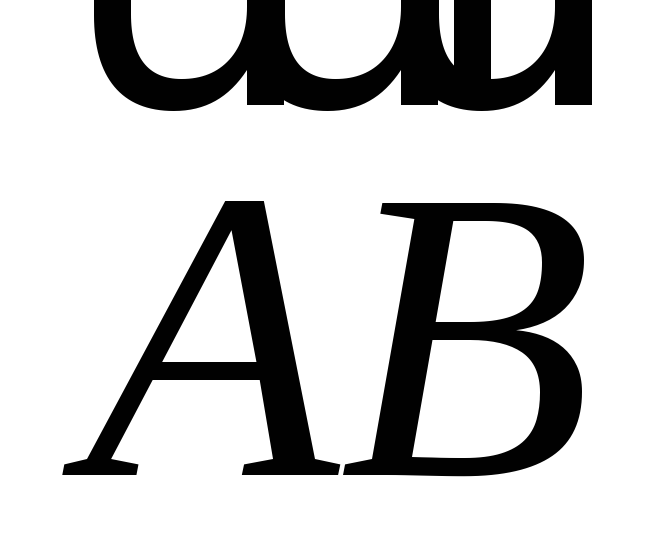 ,
найдите координаты вершин трапеции и
точкиS
пересечения боковых сторон.
,
найдите координаты вершин трапеции и
точкиS
пересечения боковых сторон.Найдите единичный вектор, сонаправленный вектору
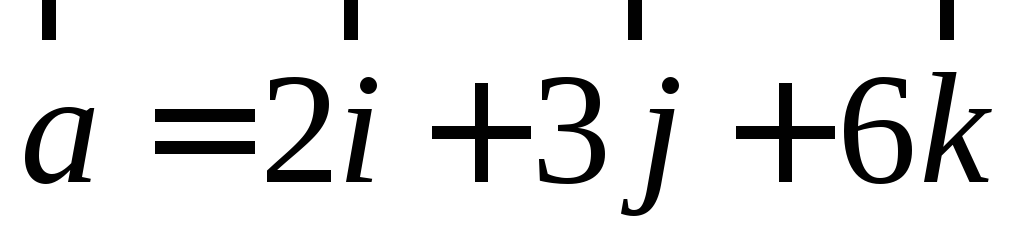 .
.Какой угол образуют единичные векторы
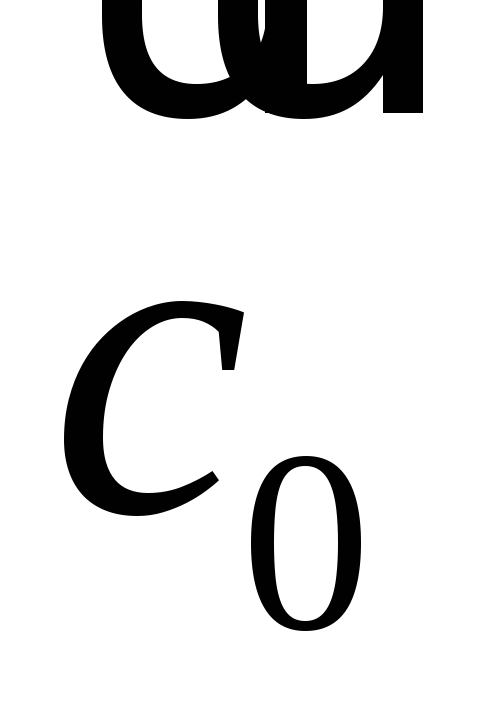 и
и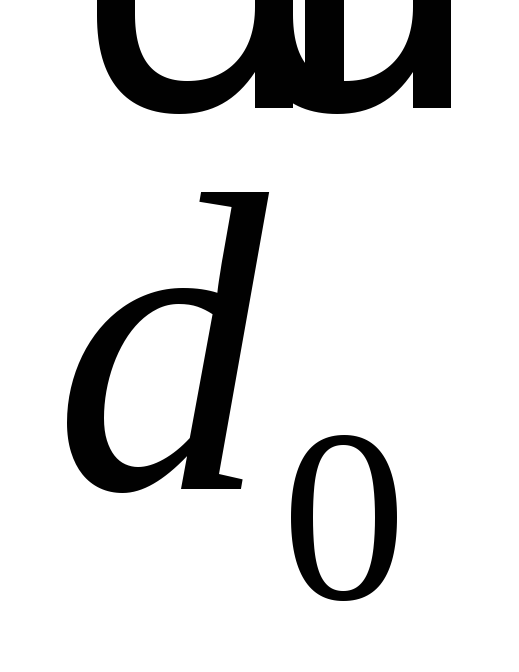 ,
если известно, что векторы
,
если известно, что векторы и
и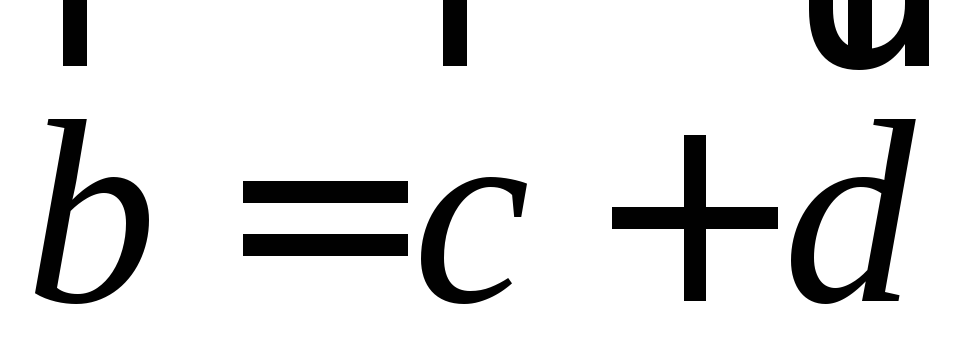 ортогональны?
ортогональны?Найдите координаты вершин треугольника, если даны уравнения двух его сторон
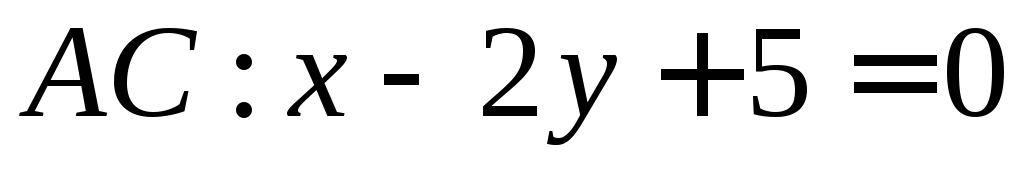 ,
,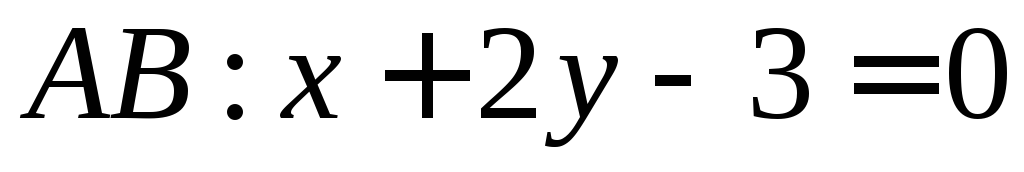 и двух высот:
и двух высот: ,
,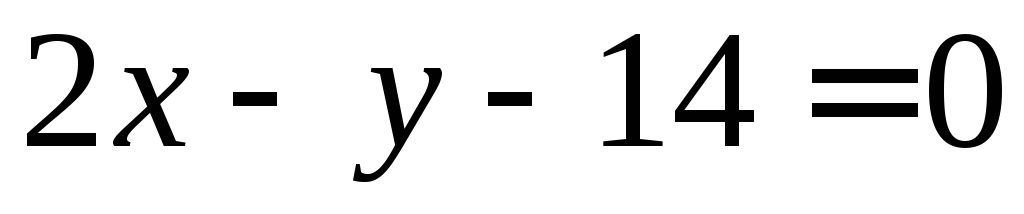 .
.Постройте кривую

Приведите кривую
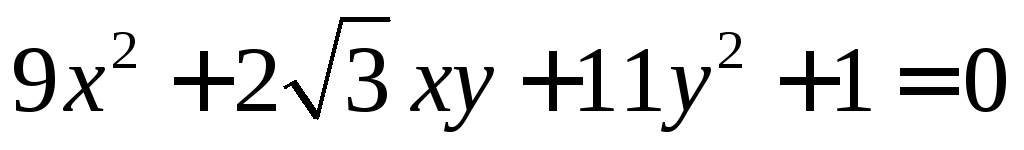 к каноническому виду.
к каноническому виду.Найдите точку, симметричную точке
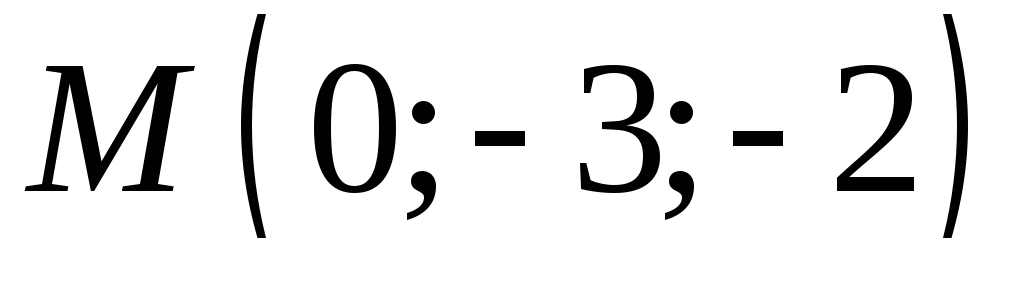 относительно плоскости
относительно плоскости
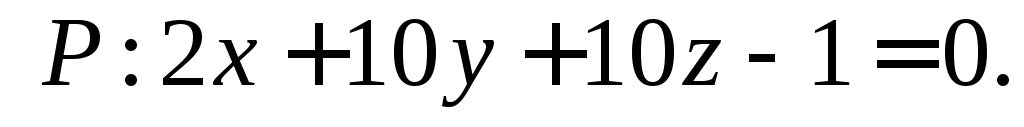
Составьте уравнение плоскости, которая проходит через точку M (1;-1;4) перпендикулярно к двум плоскостям:
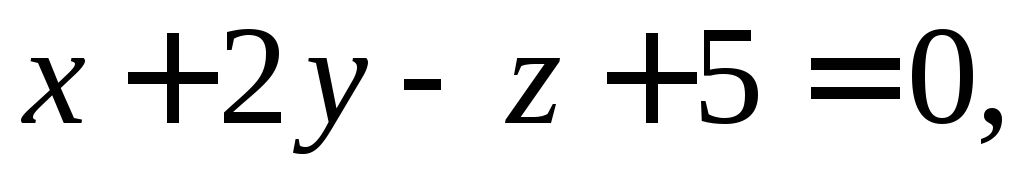 и
и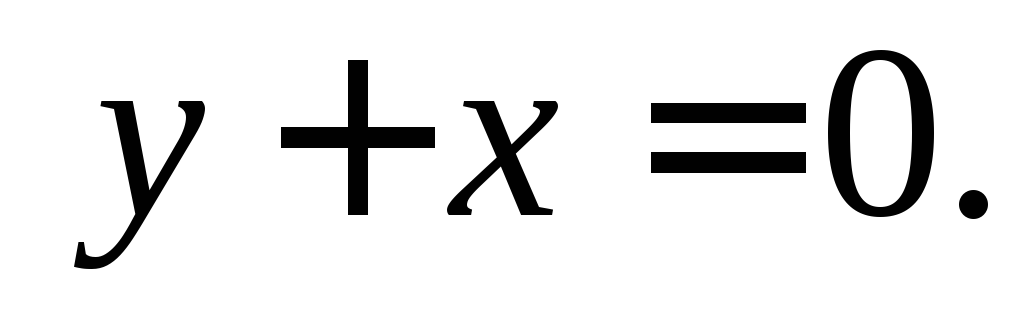
Составьте уравнение плоскости, проходящей через прямую
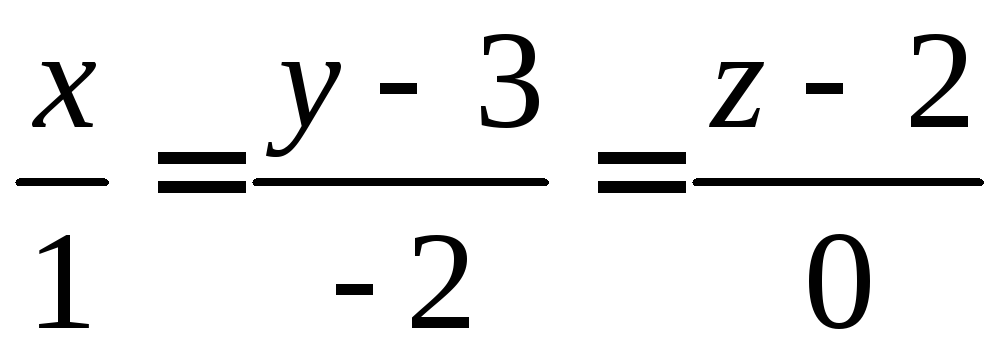 перпендикулярно к плоскости
перпендикулярно к плоскости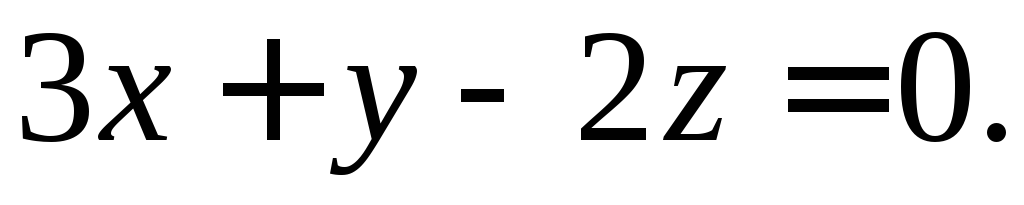
Найдите угол между прямыми
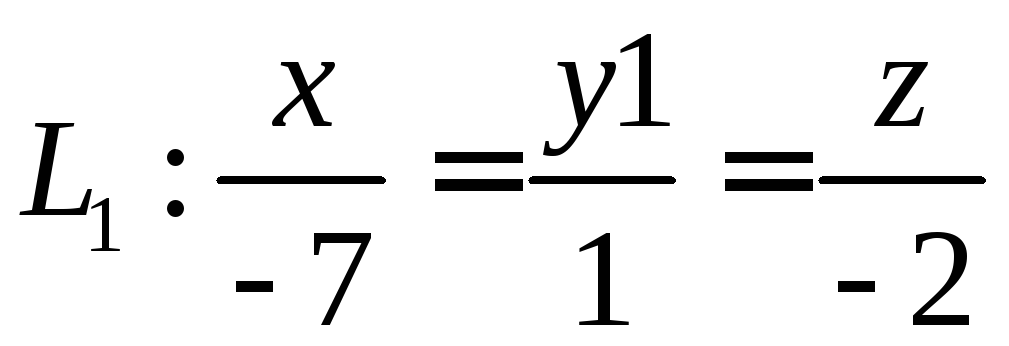 и
и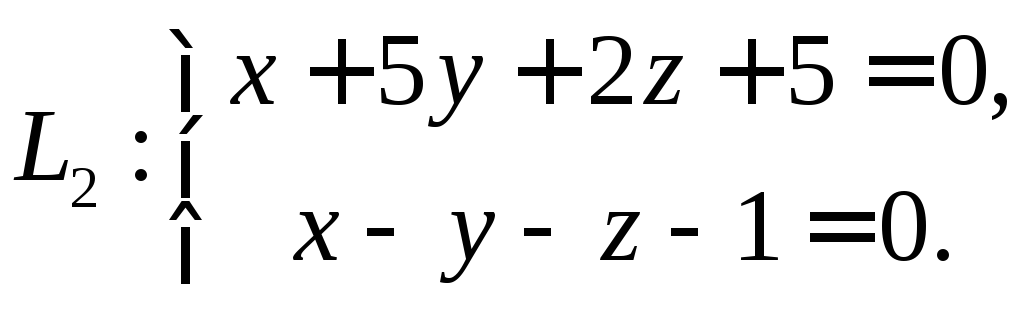
Составьте уравнение сферы, если известны координаты ее центра C (1;1;0) и то, что плоскость
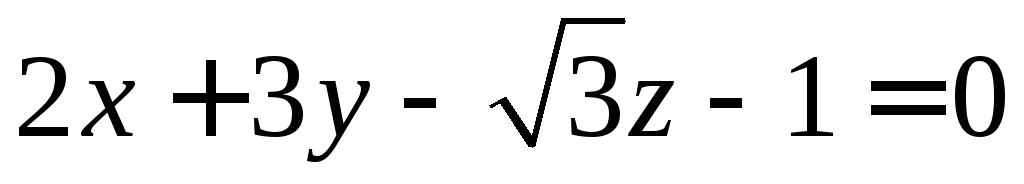 касается сферы.
касается сферы.Найдите уравнения линий пересечения поверхности
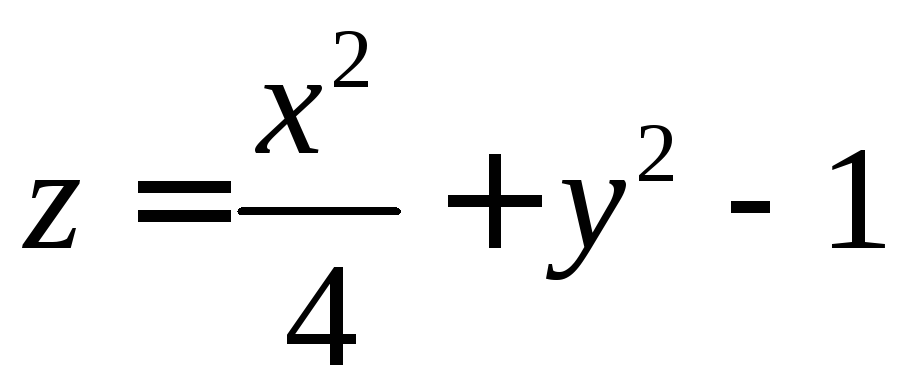 с координатными плоскостями.
с координатными плоскостями.
Вариант 25
Дан треугольник АВС. На стороне ВС расположена точка М так, что
|BM|
: |MC|
= λ.
Найдите вектор
![]() ,
если
,
если
![]() .
.
Даны векторы
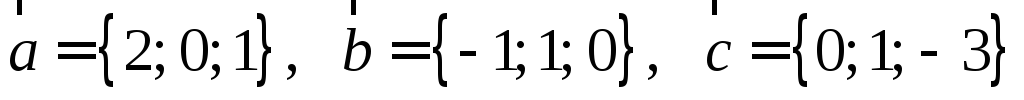 .
Вычислите
.
Вычислите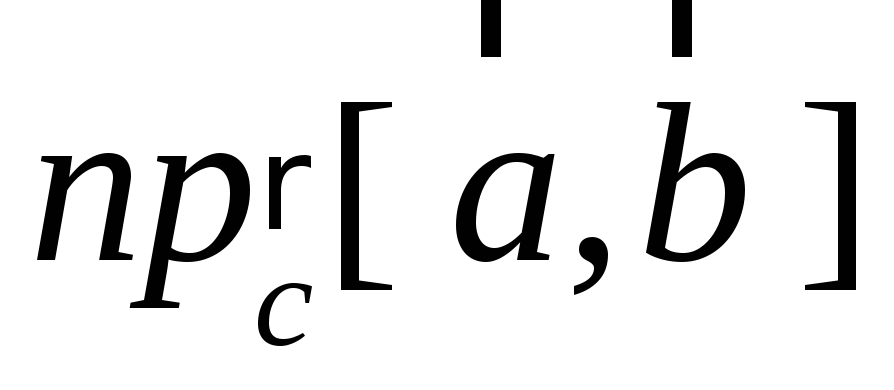 .
.Даны векторы
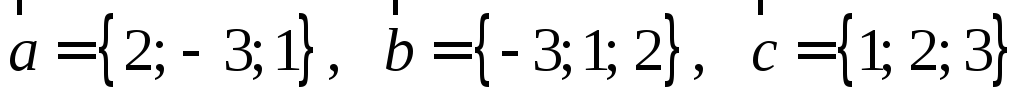 .
Вычислите
.
Вычислите и
и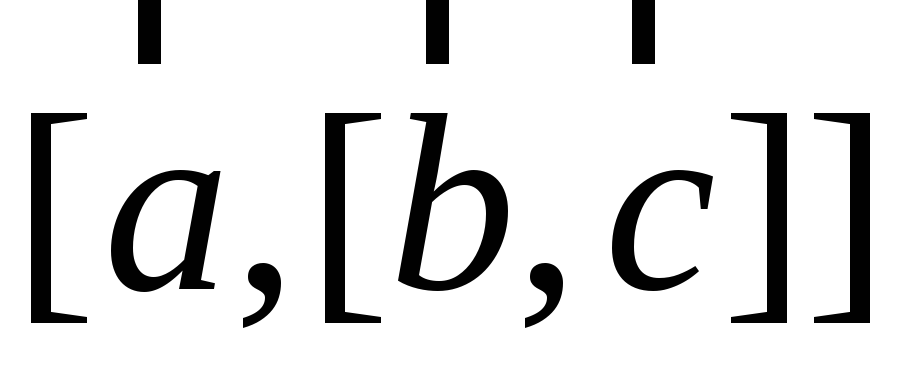 .
.Найдите уравнения и длины сторон и медиан треугольника,если даны две его вершины А (-1; -2), В (19; -12) и точка М (29/3; -10/3) пересечения его медиан.
Постройте кривую

Приведите кривую
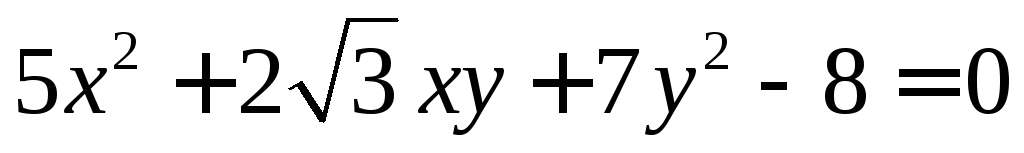 к каноническому виду.
к каноническому виду.Найдите точку, симметричную точке
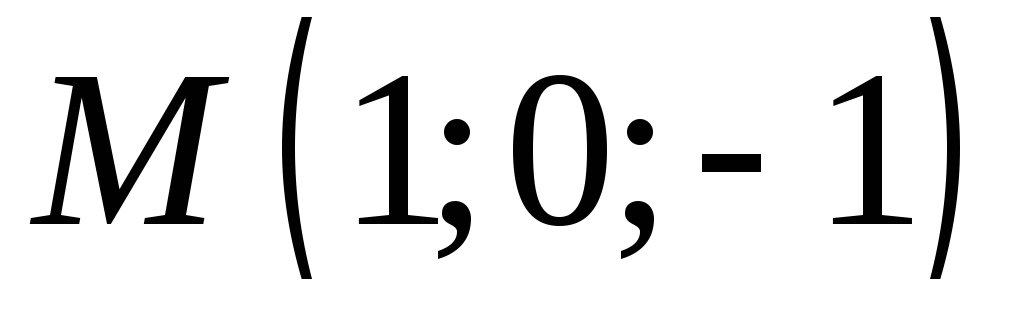 относительно
плоскости
относительно
плоскости
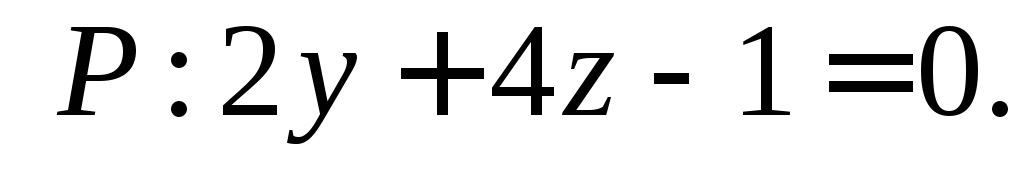
Определите двугранный угол, образованный пересечением пары плоскостей
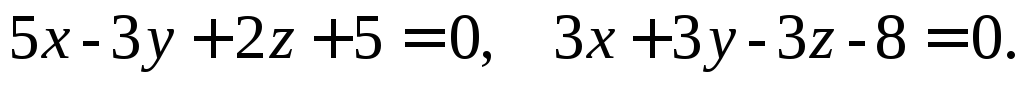
Вычислите кратчайшее расстояние между прямыми:
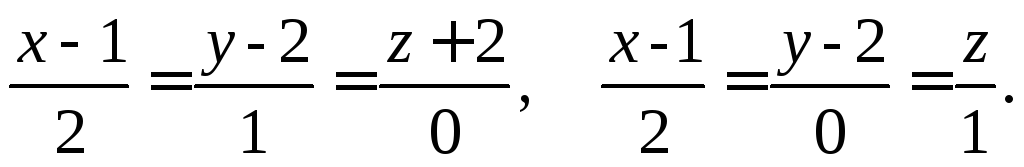
Составьте уравнения проекции прямой L:
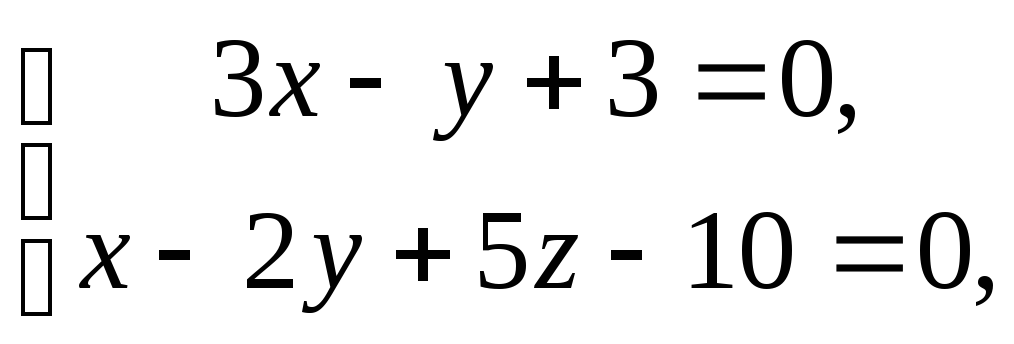 на плоскостьP:
на плоскостьP: .
.Составьте уравнение сферы, если известно, что точки
 лежат на сфере.
лежат на сфере.Найдите уравнения линий пересечения поверхности
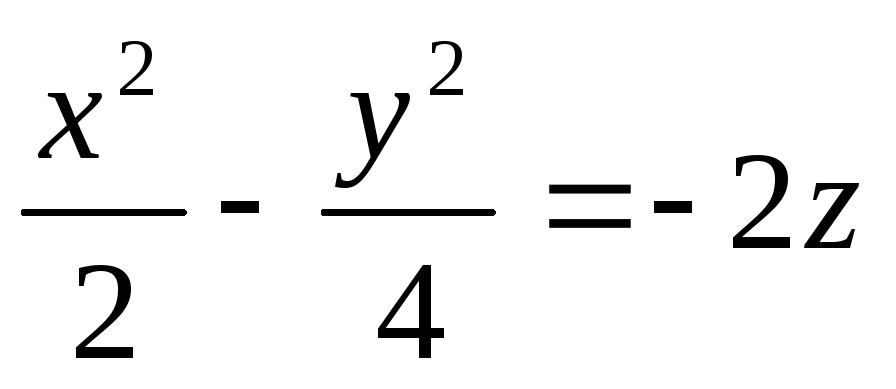 с координатными плоскостями.
с координатными плоскостями.
