Вариант 19

1. Даны три точки О, А и В, не лежащие на одной прямой. Принимая за базисные векторы и, найдите координаты вектора , если точка N лежит на прямой АВ вне отрезка АВ и .

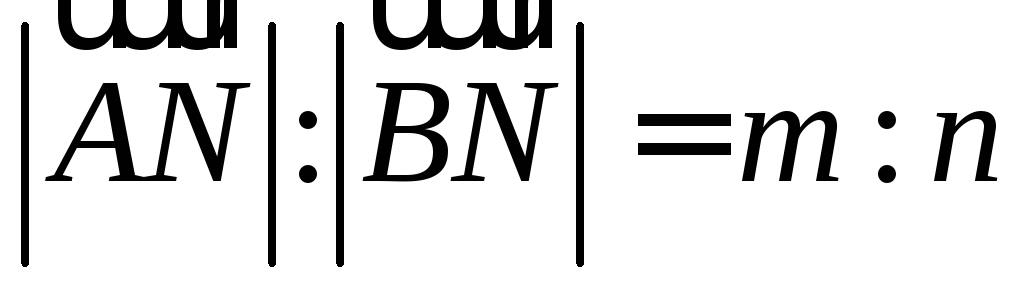2. Пусть отличные от нуля векторы ортогональны. При каком значении параметра вектор ортогонален вектору?

3. Вычислите высоту параллелепипеда, построенного на трех векторах , если за основание взят параллелограмм, построенный на векторах. Кроме того, известно, что- взаимно перпендикулярные орты.

4. Найдите координаты вершин треугольника, если даны уравнения двух его сторон ,и двух его высот:,.

5. Постройте кривую .

6. Приведите кривую к каноническому виду.

7. Найдите точку, симметричную точке относительно плоскости

8. Составьте уравнение плоскости, которая проходит через точку перпендикулярно к двум плоскостям:,.

9. Составьте уравнение плоскости, проходящей через прямую перпендикулярно к плоскости

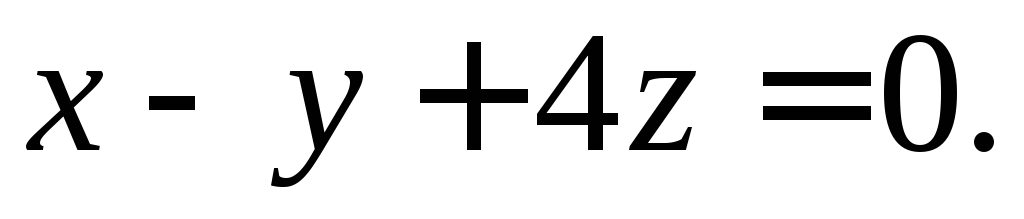
10. Найдите угол между прямыми и

11. Составьте уравнение сферы, если известны координаты ее центра

C (1;0;1) и то, что плоскость касается сферы.

12. Найдите уравнения линий пересечения поверхности с координатными плоскостями.

Вариант 20

1. Дан правильный шестиугольник OABCDE со стороной ОА = 3. Обозначим ,и. Установите зависимость между ними. Выразите через и векторы .

2. Докажите, что если диагонали четырехугольника в точке пересечения делятся пополам, то этот четырехугольник - параллелограмм.

3. Найдите длину вектора , если, а угол между векторамиравен 60.

4. Найдите уравнения и длины сторон и медиан треугольникаесли даны две его вершины А (-1, 2), В (-11, 7) и точка М (19/3;8/3) пересечения его медиан.

5. Постройте кривую .

6. Приведите кривую к каноническому виду.

7. Найдите точку, симметричную точке относительно плоскости

8. Найдите угол между плоскостями ,.

9. Вычислите кратчайшее расстояние между прямыми:

10. Составьте уравнения проекции прямой на плоскость.

11. Составьте уравнение сферы, если известно, что точки лежат на сфере.

12. Найдите уравнения линий пересечения поверхности с координатными плоскостями.

Вариант 21

1. Вне плоскости параллелограмма ABCD взята точка О. В базисе из векторов найти координаты вектора, еслиК – середина стороны AD.

2. Найти направляющие косинусы вектора .

3. Составляют ли векторы ортогональный базис трехмерного пространства?

4. Найдите уравнения и длины сторон и медиан треугольника, если даны три его вершины А (1; -2), В (-9; 3), С (-5; -5).

5. Постройте кривую

6. Приведите кривую к каноническому виду.

7. Найдите точку, симметричную точке относительно плоскости

8. Точка служит основанием перпендикуляра, опущенного из начала координат на плоскость. Составьте уравнение этой плоскости.

9. Найдите проекцию точки М (2;1;0) на плоскость P: y + z + 2 = 0.

10. Докажите, что прямая лежит в плоскости.

11. Составьте уравнение сферы, если известны координаты ее центра C (1;-2;0) и радиус R = 3.

12. Найдите уравнения линий пересечения поверхности с координатными плоскостями.