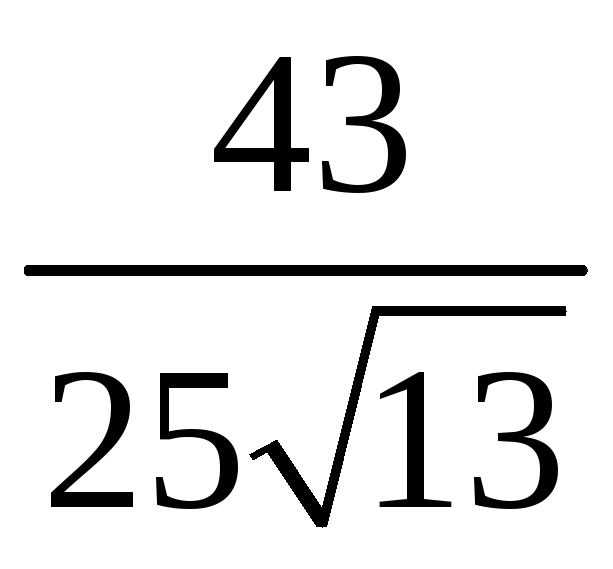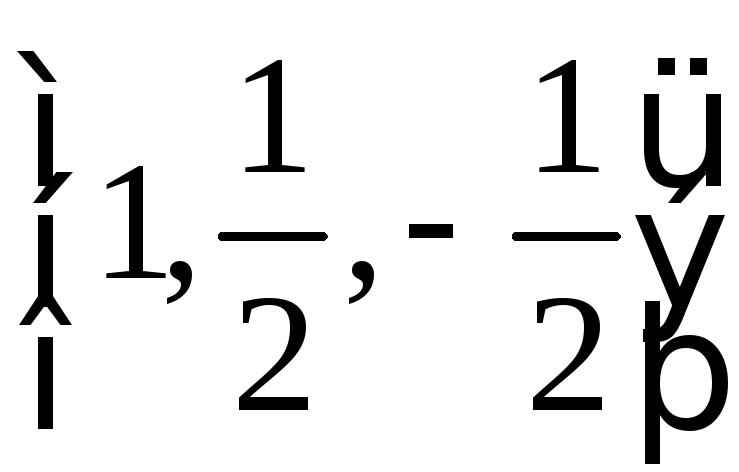- •Домашние задания Дз № 1. Векторная алгебра
- •Дз № 2. Прямая и плоскость
- •Дз №3. Прямая на плоскости
- •Дз № 4. Кривые на плоскости
- •Дз № 5. Поверхности в пространстве
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •8. Пример вариантов контрольных работ Векторная алгебра
- •Аналитическая геометрия
Домашние задания Дз № 1. Векторная алгебра
Сборник задач по математике для втузов: В 4 ч. Ч. 1: Векторная алгебра и аналитическая геометрия. Определители и матрицы системы линейных уравнений. Линейная алгебра. Основы общей алгебры / А. В. Ефимов, А. Ф. Каракулин, И. Б. Кожухов [и др.]; под ред. А. В. Ефимова, А. С. Поспелова. 4-е изд., перераб. и доп. - М.: Физматлит, 2003. - 288 с.: ил.; 21 см. - ISBN 5-940520-34-0.
|
№ п/п |
№ по Еф. |
Задание |
Ответ |
| |||
|
1 |
1.11 |
ABCDEF
- правильный шестиугольник, причем
|
|
| |||
|
2 |
1.18 |
На
стороне
|
|
| |||
|
3 |
1.19 |
Разложить
вектор
|
|
| |||
|
4 |
1.27 |
В
тетраэдре ОАВС
медиана AL
грани АВС
делится точкой М
в отношении
|
|
| |||
|
5 |
1.35 а-г |
Заданы
векторы
|
а)
|
| |||
|
6 |
1.39 |
Заданы
векторы
|
а)
|
| |||
|
7 |
1.43 |
Найти
вектор |
|
| |||
|
8 |
1.44 |
Найти
вектор |
|
| |||
|
9 |
1.46 |
При
каких значениях
|
|
| |||
|
10 |
1.38 |
Показать,
что тройка векторов
|
|
| |||
|
11 |
1.65в |
|
13 |
| |||
|
12 |
1.66 |
|
|
| |||
|
13 |
1.67 |
Вычислить
длину диагоналей параллелограмма,
построенного на векторах
|
|
| |||
|
14 |
1.69 |
В
треугольнике АВС
|
|
| |||
|
15 |
1.72 |
Найти
угол, образованный единичными векторами
|
|
| |||
|
16 |
1.78 г, ж, з, и |
Даны
векторы
|
г)
|
| |||
|
17 |
1.79 |
Даны
точки
|
| ||||
|
18 |
1.81 |
Для
заданных векторов
|
а)
| ||||
|
19 |
1.83 |
Найти
косинус угла
|
| ||||
|
20 |
1.88 |
Найти
координаты вектора
|
| ||||
|
21 |
1.89 |
Вектор
|
| ||||
|
22 |
1.98 в |
|
в)
| ||||
|
23 |
1.100 г |
Упростить
выражение
|
г) 3 |
|
24 |
1.102 |
|
|
|
25 |
1.106 в |
Заданы
векторы
|
в)
|
|
26 |
1.108 |
В
треугольнике с вершинами А(1,-1,2),
В(5,-6,2)
и С(1,3,-1)
найти высоту
|
5 |
|
27 |
1.109 |
Определить,
при каких значениях
|
|
|
28 |
1.111 |
Для
заданных векторов
|
|
|
29 |
1.113 |
Найти
вектор
|
|
|
30 |
1.118 |
Найти
координаты вектора
|
|
|
31 |
1.125 |
Векторы
|
-3 |
|
32 |
1.126 |
Заданы
векторы
|
- 7; а) левая, б) правая, в) правая |
|
33 |
1.127 б |
Установить,
образуют ли векторы
|
б) да |
|
34 |
1.134 |
В
тетраэдре с вершинами в точках А(1,1,1),
В(2,0,2),
С(2,2,2)
и D(3,4,-3)
вычислить высоту
|
|
|
35 |
1.136 б |
При
каком
|
б)
при любом
|
|
36 |
1.138 б |
Найти координаты четвертой вершины тетраэдра АВСD, если известно, что она лежит на оси Оу, А(0,1,1), В(4,3,-3), С(2,-1,1), а объем V тетраэдра равен двум. |
б)
|

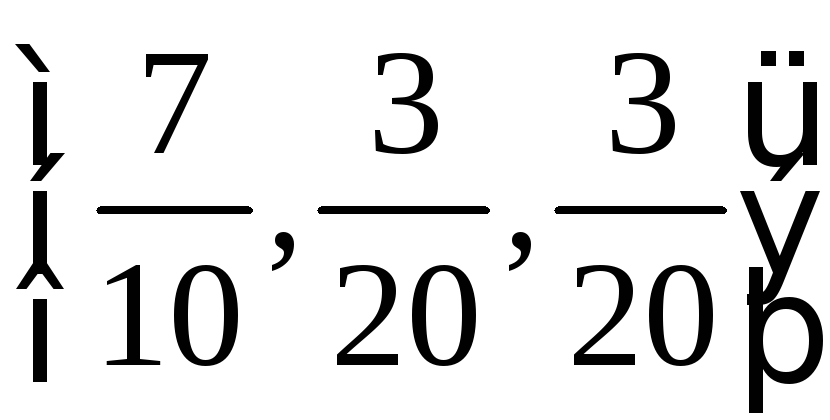
 ;
б)
;
б) ;
в)
;
в) ;
б)
;
б) ;
в)
;
в)