Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Красноярский институт железнодорожного транспорта, филиал ИрГУПС

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методичка по практич. ЖДСУ

.pdf

Скачиваний:

400

Добавлен:

15.02.2015

Размер:

480.29 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Таблица 1, г – Исходные данные:

Радиусы сопрягающих кривых соответствуют переводным кривым

Исходные данные			Вариант (последняя цифра шифра)
	1	2	3	4	5	6	7	8	9	0
Тип рельса, пути: 1	Р65	Р65	Р50	Р50	Р65	Р50	Р65	Р50	Р50	Р50
2	Р65	Р50	Р65	Р65	Р50	Р50	Р65	Р50	Р65	Р50
3	Р50	Р65	Р50	Р65	Р50	Р65	Р65	Р50	Р50	Р50
4	Р50	Р50	Р50	Р65	Р50	Р50	Р65	Р50	Р50	Р65
5	Р50	Р50	Р65	Р65	Р50	Р50	Р50	Р65	Р65	Р65
6	Р50	Р50	Р65	Р50	Р50	Р65	Р50	Р50	Р65	Р65
7	Р50	Р50	Р50	Р65	Р50	Р65	Р50	Р50	Р50	Р65
Марки крестовин: 1	1/9	1/11	1/9	1/9	1/11	1/9	1/11	1/9	1/9	1/9
2	1/11	1/9	1/9	1/11	1/9	1/9	1/11	1/9	1/11	1/9
3	1/11	1/11	1/9	1/9	1/11	1/11	1/11	1/9	1/11	1/9
4	1/9	1/9	1/11	1/11	1/9	1/9	1/9	1/11	1/9	1/9
5	1/11	1/9	1/9	1/9	1/9	1/11	1/9	1/9	1/9	1/9
6	1/9	1/9	1/9	1/9	1/11	1/9	1/9	1/9	1/9	1/11
Междупутье, м е1-2	6,5	7,5	5,3	5,3	7,5	5,3	6,5	5,3	6,5	5,3
е2-3	5,3	5,3	5,3	5,3	5,3	7,5	5,3	6,5	5,3	5,3
е3-4	7,5	5,3	5,3	6,5	6,5	5,3	5,3	5,3	5,3	6,5
е4-5	5,3	4,8	6,5	5,3	5,3	4,8	5,3	6,5	6,5	5,3
е5-6	5,3	5,3	5,3	5,3	5,3	6,5	5,3	5,3	5,3	5,3
е6-7	5,3	6,5	4,8	5,3	5,3	5,3	5,3	6,5	5,3	4,8

Таблица 1, д – Исходные данные:				Все		рельсы типа Р50, все					стрелочные
переводы марки 1/9, радиусы сопрягающих кривых R=200 м. Рекомендуемый
масштаб построения 1:1000
Исходные данные			Вариант (последняя цифра суммы шифра)
	1	2	3		4		5	6	7	8		9	0
Междупутье, м е1-2	6,5	7,5	5,3		5,3		6,5	5,3	6,5	5,3		6,5	5,3
е2-3	5,3	5,3	5,3		5,3		5,3	7,5	5,3	6,5		5,3	5,3
е3-4	6,5	5,3	5,3		6,5		6,5	5,3	5,3	5,3		5,3	6,5
е4-5	5,3	6,5	6,5		5,3		5,3	5,3	5,3	6,5		6,5	5,3
е5-6	5,3	5,3	5,3		5,3		5,3	6,5	5,3	5,3		5,3	5,3

Таблица 1, е – Исходные данные для комбинированной стрелочной улицы (рис.14). Радиусы сопрягающих кривых соответствуют переводным кривым

Исходные данные			Вариант (последняя цифра шифра)
	1	2	3	4	5	6	7	8	9	0
Тип рельса, пути: 1	Р65	Р65	Р50	Р50	Р65	Р50	Р65	Р50	Р50	Р50
2	Р65	Р50	Р65	Р65	Р50	Р50	Р65	Р50	Р65	Р50
3	Р65	Р65	Р50	Р65	Р50	Р65	Р65	Р50	Р50	Р50
4	Р50	Р50	Р50	Р65	Р50	Р50	Р65	Р50	Р50	Р65
5	Р65	Р50	Р65	Р65	Р50	Р50	Р50	Р65	Р65	Р65
6	Р65	Р50	Р65	Р50	Р50	Р65	Р50	Р50	Р65	Р65
7	Р50	Р50	Р50	Р65	Р50	Р65	Р50	Р50	Р50	Р65
8	Р50	Р50	Р50	Р50	Р50	Р50	Р65	Р50	Р50	Р50
9	Р50	Р65	Р50	Р65	Р65	Р65	Р65	Р50	Р65	Р50
10	Р50	Р50	Р65	Р65	Р65	Р65	Р65	Р50	Р50	Р50
Марки крестовин: 1	1/11	1/11	1/11	1/9	1/11	1/9	1/9	1/9	1/9	1/9
2	1/11	1/9	1/9	1/9	1/9	1/9	1/9	1/9	1/11	1/11
3	1/9	1/11	1/9	1/9	1/11	1/11	1/11	1/11	1/11	1/11

4	1/9	1/11	1/9	1/9	1/11	1/9	1/11	1/9	1/9	1/9
5	1/11	1/9	1/9	1/11	1/9	1/9	1/11	1/9	1/11	1/9
6	1/11	1/11	1/9	1/9	1/11	1/11	1/11	1/9	1/11	1/9
7	1/9	1/9	1/11	1/11	1/9	1/9	1/9	1/11	1/9	1/9
8	1/11	1/9	1/9	1/9	1/9	1/11	1/9	1/9	1/9	1/9
9	1/9	1/9	1/9	1/9	1/11	1/9	1/9	1/9	1/9	1/11
Междупутье, м е1	6,5	7,5	5,3	5,3	7,5	5,3	6,5	5,3	6,5	5,3
е2	5,3	5,3	5,3	5,3	5,3	7,5	5,3	6,5	5,3	5,3
е3	7,5	5,3	5,3	6,5	6,5	5,3	5,3	5,3	5,3	6,5
е4	5,3	4,8	6,5	5,3	5,3	4,8	5,3	6,5	6,5	5,3
е5	5,3	5,3	5,3	5,3	5,3	6,5	5,3	5,3	5,3	5,3
е6	5,3	6,5	4,8	5,3	5,3	5,3	5,3	6,5	5,3	4,8
е7	6,5	6,5	5,3	7,5	5,3	5,3	5,3	5,3	6,5	5,3
е9	5,3	5,3	5,3	5,3	5,3	7,5	7,5	5,3	5,3	5,3
е10	7,5	7,5	5,3	6,5	6,5	5,3	5,3	6,5	5,3	4,8

Примечание: прямые вставки (d) при расчете взаимного расположения принимаются студентом, согласно нормам проектирования, самостоятельно.

ПРАКТИЧЕСКАЯ РАБОТА №5

Расчет параллельного смещения пути

Цель работы: получить навыки расчета параллельного смещения путей в двух случаях – с переходной кривой и без нее.

Задача практической работы:

рассчитать параметры смещения пути с переходной кривой; рассчитать и построить в масштабе 1:2000 параллельное смещение без

переходной кривой.

Параллельное смещение путей (рис. 16) предусматривается на станциях при их сооружении или реконструкции для уширения междупутий под установку опор контактной сети, освещения и размещения пассажирских платформ. Чаще всего смещение пути производится с междупутий 4,1 (на перегоне) или 4,8 до 5,3 – 6,5 м и более. Для плавности движения поездов по смещенным путям применяют обратные кривые (S-образные) кривые больших радиусов (3000 – 4000 м при смещении главных путей).

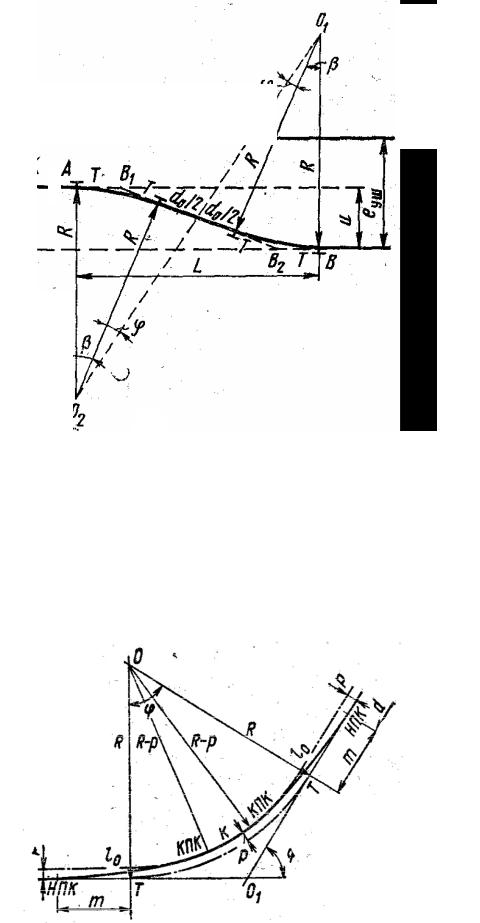
Рисунок 16 – Уширение междупутья е1 до величины еуш

Чтобы обеспечить плавность движения, между прямыми участками и круговыми кривыми, устраивают переходные кривые (рис. 17), которые имеют ту особенность, что их кривизна (т.е. величина, обратная радиусу) не является постоянной, а нарастает постепенно от бесконечно малой в точке примыкания к прямому участку до значения радиуса в точке слияния с круговой кривой. В начале переходной кривой радиус ρ = ∞, а в конце он снижается до радиуса кривой ρ = R.

Рисунок 17 – Сопряжение прямого участка с прямой вставкой d при наличии переходных кривых

НПК – начало переходной кривой; КПК – конец переходной кривой

Пример 1: Рассчитать длину участка в кривой с устройством переходной кривой (рис. 17). Радиус круговой кривой R = 3000 м, длина переходной кривой имеет обратную зависимость от длины радиуса круговой кривой и принимается равной l0 = 40 м, прямая вставка d0 = 75 м. Величина смещения пути u = 2,2 м.

Решение: По величинам R и l0 вычисляем величину смещения (сдвижки) круговой кривой

ρ	=		l02		(1 -			l02		+					l04		)	=	402		(1 -				402	+		404	) =
		24R						112R 2				21120R 4							24 × 3000						112 × 30002		21120 × 30004
=	1600				(1 -		1600						+	2560000						) = 0,022 м;

	72000					100,8 × 107									171072 × 1013
и увеличение m тангенса О1Т
			l	0				l 2						l 4				40	1600				2560000
m =					(1 -		0		+					0		) =			(1 -					+				) = 19,99 м;
						120R 2					17280 R 4
		2																2	108 × 10			7	139968 × 1013

В этом случае длина переходного участка

L = 2 (R + ρ) sin φ + (d0 + 2m) cos φ + 2m;

tg φ = d0 / 2R = 75 / 2*3000 = 0,012500, φ = 0,7162º = 0º42’58”

L = 2 (3000 + 0,022) 0,01249972 + (75 + 2*19,99) 0,999922 + 2*19,99 = 229,95 м.

Длины каждого криволинейного участка и тангенсов Т могут быть найдены по формулам:

К = 0,017453 Rφ + l0 = 0,017453*3000*0,72º + 40 = 77,70 м;

Т = (R + ρ) tg φ/2 + m = (3000 + 0,022)0,006283 + 19,99 = 38,84 м.

Пример 2: Рассчитать параллельное смещение одного пути при переходе из междупутья 5,3 м к междупутью 7,5 м (рис. 16) для размещения пассажирской платформы. Радиус сопрягающей кривой 3000 м. Прямая вставка между концами круговых кривых 75 м. Без устройства переходных кривых.

Решение: Проецируя на вертикальную ось контур АО1О2В, получим

О1О2cos (β + φ) = 2R – u,						но
О1О2 = 2R / cos φ;			tg φ = d0 / 2R, откуда
(2R/ cos φ) cos (β + φ) = 2R – u,								т.е.
cos (β + φ) = [(2R – u) / 2R] cos								φ;
tg φ = 75 / 2*3000 = 0,012500, φ = 0,72º = 0º43’.
Тогда cos (β + φ) = (1 -					u			2,2
						) cos φ = (1 -			) 0,999921 = 0,999554
					2R
								2 × 3000
β + φ = 1,71º = 1º42’41”;						β = 1,71º - 0,72º = 0,9922º = 0º59’28”.
Определив угол β, находим:
	β			0,9922O
T = R tg		= 3000 tg					= 25,98 ;

2			2

К = 0,017453*R*βº = 0,017453*3000*0,9922º = 51,95м;

L = 2T + (2T + d0) cos β = 2*25,98 + (2*25,98 + 75) cos 0,9922º = 178,90 м; L = 2R sin β + d0 cos β = 2*3000*0,0173163 + 75*0,99985 = 178,89 м.

Делаем проверку правильности расчетов по формуле u - (2Т + d0) sin φ = 0

2,2- (2*25,98+75) 0,0173163 = 0

2,2 - 2,1985 = 0,0015 ≈ 0

Таблица 2 – Исходные данные (оба задания выполняются по одному исходному данному)

Исходные данные			Вариант (последняя цифра шифра)
	1	2	3	4	5	6	7	8	9	0
Междупутье, е, м	7,5	5,3	4,8	5,3	6,5	4,8	5,3	4,8	6,5	5,3

Междупутье, е’, м	17,1	7,5	10,3	17,1	7,5	7,5	10,3	15,9	10,6	7,5

Радиус кривой	3000	2500	3500	2500	1500	1000	2000	1800	1300	4000
сопряжения, R, м	3000	2500	3500	2500	1500	1000	2000	1800	1300	4000
Величина прямой	150	75	15	75	150	15	150	75	75	150
вставки, d0, м

ПРАКТИЧЕСКАЯ РАБОТА №6

Расчет координат основных элементов горловины станции

Цель работы: научиться рассчитывать координаты элементов горловины станции.

Задача практической работы:

-по заданной преподавателем схеме горловины, студент должен рассчитать координаты стрелочных переводов и вершин углов поворотов;

-по рассчитанным размерам построить заданную горловину в масштабе

1:2000.

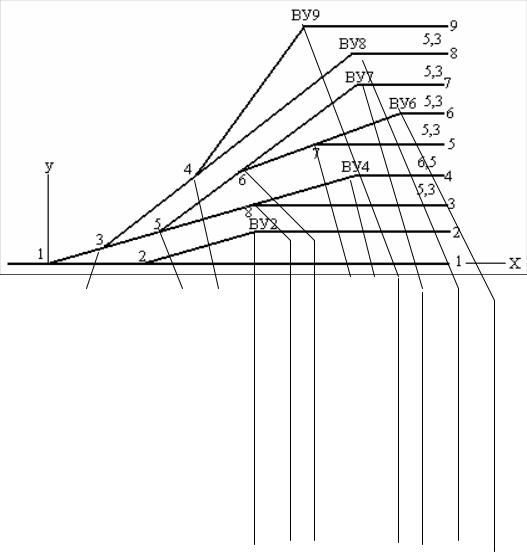
Для того чтобы определить длину горловины следует найти координаты Х и Y всех центров стрелочных переводов и вершин углов поворотов. Затем результаты координирования вносятся в таблицу (рис.18).

Для расчета координат основных точек стрелочной улицы необходимо знать тип рельс, марки крестовин и основные размеры стрелочных переводов, междупутья и радиусы сопрягающих кривых. За начало координат можно принять центр перевода 1.

6,5

10,5





Наименова	1	3	2	5	4	2	8 6		7	4		9 7		8		6
-ние точки	1	3	2	5	4	2	8 6		7	4		9 7		8		6
-ние точки	ЦП	ЦП	ЦП	ЦП	ЦП	ВУ	ЦП ЦП		ЦП	ВУ ВУ ВУ				ВУ	ВУ
	ЦП	ЦП	ЦП	ЦП	ЦП	ВУ	ЦП ЦП		ЦП	ВУ ВУ ВУ				ВУ	ВУ

Расстояние		4,279		8,624	13,841	10,50	13,937	21,544	33,304	22,30	50,00		39,40	44,70	34,10
по оси «Y»	0,00		0,00
	0,00		0,00

Расстояние		47,069	71,795	93,864	89,568	187,295	186,00	151,287	220,099	200,11	251,60		230,50	221,336	267,798
по оси «Х»	0,00
	0,00

Рисунок 18 – Координирование основных точек горловины станции (пример)

Дано:

тип рельса – путь 1, 2 – Р65;

остальные пути – Р50;

марка крестовины – стр. пер. 1, 2 – 1/11;

остальные – 1/9;

прямая вставка d – 12,5 м;

радиус сопрягающей кривой R при стр. пер.1/9 - 200 м, при 1/11 – 300 м; основные размеры стрелочных переводов (a, b, угол α - см. прил.1).

Найти:

Координаты центров переводов ЦП и вершин углов поворота ВУ комбинированной стрелочной улицы (рис.18).

Решение:

Прежде, чем находить координаты, необходимо определить прямые вставки Р и f, а также тангенсы кривых Т.

Р1-2 = Р3-5 = Р5-6 = (е / sin α) – а – b;

Р1-2 = (6,5/0,090536)-14,063-19,304 = 38,428 м; Р3-5 = (5,3/0,110433)-15,459-15,602 = 16,931 м;

Р5-6 = (6,5/0,110433)-15,459-15,602=27,798 м

	8
		∑ e - (b1	+ d1−3	+ a3	+ b3 + P3−5 + a5 ) sin a - (b5	+ P5−6	+ a6 ) sin 2a
Р6−7	=	i=4						- b6 - a7 =
Р6−7	=				sin a			- b6 - a7 =
					sin a

= 28,8 - (19,304 + 12,5 + 15,459 + 15,602 + 16,931 + 15,459)×0,110433 - (15,602 + 16,931 + 15,459) ´

					0,110433
´ 0,219506 - 15,602 - 15,459 = 39,072 м
	8		+ d1−3	+ a3 + b3 + P3−5	+ a5 )sin α
		∑e − (b1	+ d1−3	+ a3 + b3 + P3−5	+ a5 )sin α
Р5−8	=	i=2				− b5 − a8 =
Р5−8	=			sin α		− b5 − a8 =
				sin α

= 17 − (19,304 + 12,5 + 15,549 + 15,602 + 16,931 + 15,459) 0,090536 − − = 15,602 15,459 61,455м

0,090536

T2= R tg α/2 =300·0,045362=13,61 м T4=T6= R tg α/2 = 200·0,0553835=11,077 м Т7=Т8=R tg α = 200·0,111113 = 22,223 м Т9 = R tg 3α/2 = 200·0,167522=33,504 м

f2= (e/sin α)-b-T2= (10,5/0,090536)-19,304-13,61=83,062 м; f4= f6= (5,3/0,110433)-15,602-11,077=21,314 м;

+ d1−3

+ a 3 + b3 + P3−5 + a 5 ) sin α − (b5 + P5−6 + a 6 ) sin 2α

∑ ei − (b1

i=6

− b

− T

sin 2α

39,4 − (19,304 + 12,5 +14,475 +19,054 + 27,798 +14,475)0,090536 −

0,219516

− (19,054 +16,931+14,475)0,219516 −19,054 − 22,223 = 43,368 м

+ d1−3

+ a3) sin α − (b3 + d3−4 + a4 ) sin 2α

∑ ei − (b1

i=7

− b

− T =

sin 2α

= 44,7 − (19,304 +12,5 + 14,475)0,090536 − (19,054 + 12,5 +14,475)0,219516 − − 19,054

0,219516

− 22,223 = 97,237 м

		8		+ d1−3	+ a3) sin α − (b3	+ d3−4	+ a4 ) sin 2α
			∑ ei − (b1	+ d1−3	+ a3) sin α − (b3	+ d3−4	+ a4 ) sin 2α
f	9	=	i=1					− b	4	− T =
f		=						− b		− T =
					sin 3α					9
					sin 3α

= 50 − (19,304 + 12,5 + 14,475)0,090536 − (19,054 + 12,5 + 14,475)0,219516 − − 19,054

0,325898

− 33,504 = 57 м

ЦП 1 Хцп1=0

Уцп1=0

ЦП 3 Хцп3=Хцп1+(b+d1-3+a) cos α = 47,069 м Yцп3= Yцп1+(b+d1-3+a) sin α = 4,279 м

ЦП 2 Хцп2=Хцп1 +b+ Р1-2+а;

Yцп2 = 0

ЦП 5 L3-5 = b+Р3-5+a = 15,602+16,931+15,459 = 47,992 м Хцп5 = Хцп3 + L3-5 cos α = 93,864 м

Yцп5 =Yцп3 + L3-5 sin α = 8,624 м

ЦП 6 L5-6=b+P5-6+a = 15,602+27,798+15,459=58,859 м Хцп6 = Хцп5+L5-6 cos 2α = 151,287 м

Yцп6 = Yцп5+L5-6 sin 2α = 21,544 м

ЦП 4 L3-4=b+d+a = 15,602+12,5+15,459=43,561 м Xцп4 = Хцп3+L3-4cos 2α = 89,568 м

Yцп4 = Yцп3+L3-4sin 2α = 13,841 м

ЦП 8 L5-8=b+P5-8+a = 15,602+61,455+15,459=92,516 м Хцп8 = Хцп5 + L5-8 cos α =186 м

Yцп8 = Yцп5 + L5-8 sin α =13,937 м

ЦП 7 L6-7=b+P6-7+a = 15,602+39,072+15,459=70,133 м

Хцп7 = Хцп6 + L6-7 cos α =220,099 м Yцп7 = Yцп6 + L6-7 sin α =33,304 м

ВУ 2 L2-ву2=b+f2+T2=19,304+83,062+13,61=115,976 м Хву2=Хцп2+L2-ву2 cos α =187,295 м

Yву2= 10,5 м

ВУ 4 L8-ву4=b+f4+T4=15,602+21,314+11,077=47,993 м Хву4=Хцп8+L8-ву4 cos α =200,11 м Yву4=10,5+6,5+5,3=22,3 м

ВУ 6 L7-ву6=b+f6+T6=15,602+21,314 +11,077=47,993 м Хву6=Хцп7+L7-ву6 cos α =267,798 м

Yву6= ∑ e = 34,1м

i=5

ВУ 7 L6-ву7=b+f7+T7=15,602+43,368+22,223=81,193 м Хву7=Хцп6+L6-ву7 cos 2α =230,5 м

Yву7= ∑ e =39,4 м

i=6

ВУ 8 L4-ву8=b+f8+T8=15,602+97,237+22,223=135,062 м Хву8=Хцп4+L4-ву8 cos 2α =221,336 м

Yву8= ∑ e = 44,7 м

i=7

ВУ 9 L4-ву9=b+f9+T9=15,602+57+33,504=106,106 м Хву9=Хцп4+L4-ву9 cos 3α =251,6 м

Yву7= ∑ e = 50 м

i=8

ПРИЛОЖЕНИЯ

Приложение 1

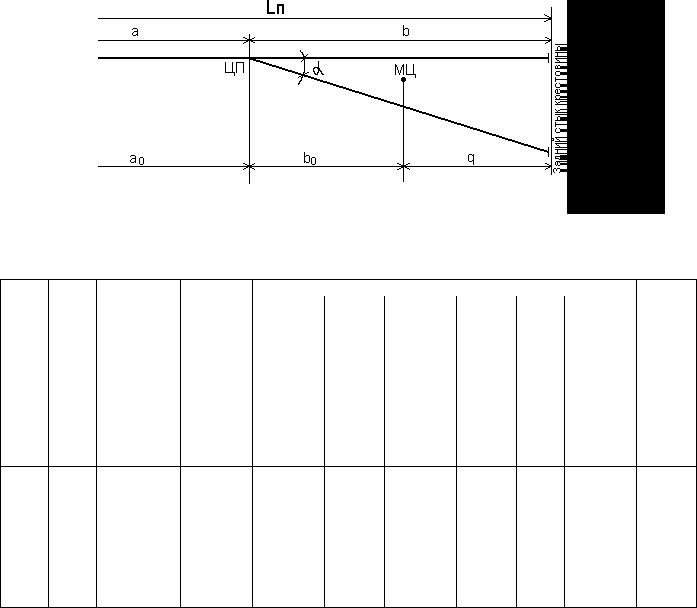
Обыкновенный стрелочный перевод

Таблица П1.1 – Основные размеры обыкновенных стрелочных переводов, м

Тип	Мар-	Угол	Радиус			Расстояние				Пол-
рель-	ка	кресто-	перево-	от оси	от	от оси	от ЦП	от	от ЦП до	ная
сов	крес-	вины	дной	перед-	начала	перед-	до МЦ	МЦ	торца	длина
	тови-		кривой	них сты-	остря-	них	кресто	крес	кресто-	стре-
	ны		(по на-	ков рам-	ков до	стыков	-вины	то-	вины	лочно-
			ружной	ных	ЦП	рамных		вины		го
			нити)	рельсов		рельсов		до ее		пере-
				до		до ЦП		зад-		вода
				начала				него
				остря-				сты-
				ков				ка

	tg α	α	R	m	a0	a=m+a0	b0	q	b=b0+q	Lп
Р65	1/22	2˚ 35´ 50´´	1444,56	5,034	26,920	31,954	33,526	5,06 0	38,586	70,540
Р65	1/18	3˚ 10´ 25´´	961,69	3,836	21,793	25,629	27,465	4,425	31,89	57,519
Р65	1/11	5˚ 11´ 40´´	300,0	2,769	11,294	14,063	16,754	2,550	19,304	33,367
Р65	1/9	6˚ 20´ 25´´	200,0	2,769	12,458	15,227	13,722	2,090	15,812	31,039
Р50	1/11	5˚ 11´ 40´´	297,26	4,327	10,148	14,475	16,754	2,300	19,054	33,529
Р50	1/9	6˚ 20´ 25´´	200,0	4,327	11,132	15,459	13,722	1,880	15,602	31,061
Р50	1/6	9˚ 27´ 45´´	200,0	2,179	7,770	9,949	9,214	1,138	10, 563	20,538

Приложение 2 Таблица П2.1 – Тригонометрические функции углов, кратных углам

крестовины

Марка	Число		Угол поворота
крестови-	стрелоч.	˚		,	,,	sin α	cos α	tg α
ны	углов	˚
ны	углов
1/11	1	5		11	40	0,090536	0,995893	0,090909
1/9	1	6		20	25	0,110433	0,993884	0,111113
1/6	1	9		27	45	0,164359	0,986401	0,166667

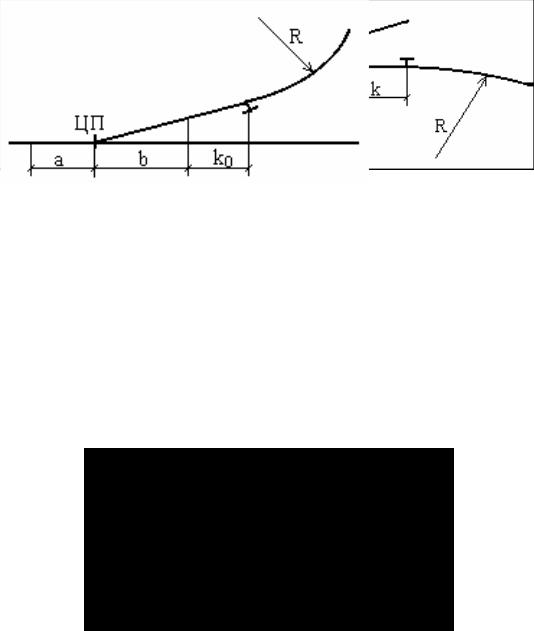
Приложение 3 Нормы проектирования взаимного размещения смежных кривых и

стрелочных переводов

Таблица П3.1 – Величина прямой вставки k

Наименование пути		Величина k при радиусе кривой, м
Наименование пути	350 и >		349 ÷ 300	299 и <
	350 и >		349 ÷ 300	299 и <
Приемо-отправочные	0		10	15
при сквозном пропуске	0		10	15
поездов
Приемо-отправочные	0		5	8
при нормальных	0		5	8
условиях
Приемо-отправочные в	0		3	5
стесненных условиях и	0		3	5
прочие станционные

Приложение 4

Таблица П4.1 – Минимальные величины прямых вставок k0, м, по

боковому неглавному пути

Тип рельсов		Величина k0 при марке крестовины
Тип рельсов	1/22	1/18	1/11	1/9	1/6
	1/22	1/18	1/11	1/9	1/6
Р65	5,86	6,46	6,17	8,50	-

Р50	-	6,46	6,16	8,10	9,77

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.08.20198.67 Mб18Метод_указ_л_р.doc
#
18.11.20193.56 Mб35Методич.указания к лабор.работам.doc
#
15.02.20151.35 Mб56методические_указания_Паскаль.doc
#
08.09.201928.39 Mб16Методическое пособие по оформлению ДП.doc
#
17.11.2019211.46 Кб1Методичка КОНТР РАБ - ПСИХОЛ И ПЕД заочники.doc
#
15.02.2015480.29 Кб400Методичка по практич. ЖДСУ.pdf
#
22.08.20191.96 Mб6методичка ПСИХОФИЗИОЛОГИЯ .doc
#
12.03.2016446.01 Кб67Методичка Салдиной.pdf
#
18.11.20195.41 Mб27Методичка-самый последний вариант.doc
#
12.03.2016373.85 Кб69Метрология.pdf
#
15.02.2015327.17 Кб71МУ для контр работ ЗО.doc