МУ к КР по ПС

Корневые устройства стрелок бывают вкладышно-накладочного типа и в виде нормального (в большинстве случаев стандартного) стыка, при- меняемого при гибких остряках

3.2 Расчет основных параметров крестовины

где S0 = 1520 мм,

tgφ = R"−G

где d = D + 1000;

D, G – параметры, зависящие от типа рельса и конструкции крестовины.

Угол крестовины определяется по формуле:

α = φ − arcsin C sin φ

Тангенс угла a называется маркой крестовины и стрелочного перевода и обозначается 1/N, где N - число марки. Например, угол a по формуле (3.13)

равен 3°59'40,3". Определим марку крестовины: N = 1/tg(3°59'40,3") = 14,32; округляем N до целого числа, в большую сторону, т.е. N = 15, сле- довательно, марка крестовины 1/15.

Уточняем угол a = arctg(1/15) = arctg(0,066667) = 3.81409°, следова-

тельно, угол a = 3о 48' 50,7". Уточненный угол a используется в дальнейших расчетах.

3.3 Расчет основных деталей стрелочного перевода

Расчет длины остряков

Длина криволинейного остряка определяется по формуле:

Длина прямолинейного остряка:

Расчет длины рамного рельса. Раскладка брусьев под стрелкой.

Рамными называются рельсы, которые служат основой стрелки и отлича-ются от стандартных наличием крепёжных отверстий, а также подстрожкой боковой грани головки рельса для укрытия остряка от удара подрезанных гребней колёс подвижного состава.

Длина рамного рельса определяется по формуле:

где m1 – передний вылет рамного рельса

l'0 – проекция остряка на направление рамного рельса m2 – задний вылет рамного рельса

По условиям раскладки переводных брусьев и расположения начала остряка со сдвижкой его относительно оси бруса на величину k (Рисунок 3.3) передний вылет

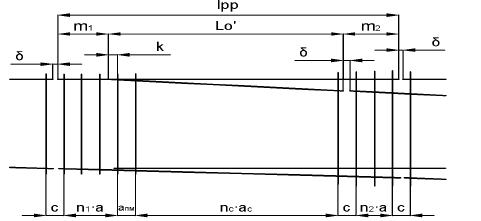
где n1 – число пролетов величиной а (1/9, 1/11, 1/18, и 1/22 принимают соответственно 5,5,7,9 пролетов)

а – величина пролета у стрелки (а=500 мм)

с– стыковой пролет (для Р50 = 440 мм, Р65,Р75 = 420 мм)

δ– стыковой зазор (8 мм)

к – смещение начала остряка относительно оси переводного бруса

к = 41мм.

где n2 - число пролетов под задним вылетом рамного рельса (принима- ем от 2 до 4, чтобы их взаимное расположение не мешало их монтажу, и чтобы ударно-динамические воздействия на один стык при проходе через него колес подвижного состава не влиял на работу другого стыка)

Рисунок 3.3 – Схема для определения длины рамного рельса

Длина остряка по условиям раскладки брусьев:

где n – число пролетов под остряком

апм - пролет, в котором располагается электропривод ( 635 мм) Количество пролетов под остряком определяется по следующей зави-

симости:

Для равномерного распределения брусьев под стрелкой допускается корректировка принятого при проектировании пролета a в пределах 5-10 %.

3.4 Расчет координат переводной кривой

За начало координат принимают точку, лежащую на рабочей грани рамного рельса против корня остряка (рис. 3.4). Абсциссы Х принимают последовательно, через 2 м. Конечную абсциссу определяют по формуле:

где хп- абсциссы точек переводной кривой, принимаемый равными

2,4,6,8…n,м.

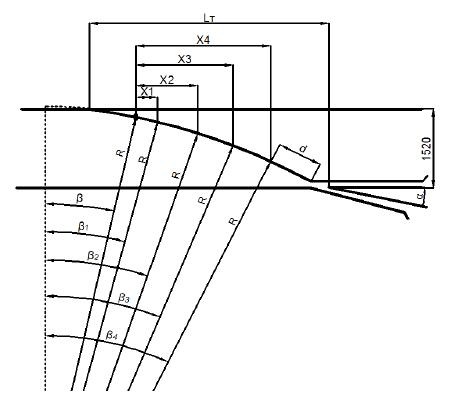
Рисунок 3.4 - Схема для определения координат переводной кривой

Для вычисления ординат составляют таблицу, в которую вводят окончательные результаты расчета.

Таблица расчета ординат переводной кривой.

Прямую вставку d перед крестовиной устраивают для того, чтобы:

1)обеспечить прямолинейное направление движения колес экипажа еще до входа в горло крестовины;

2)удалить возможный при выходе из кривой удар колес от переднего стыка крестовины и усовика;

3)избежать изгиба усовика;

4)иметь одинаковые в плане контррельсы по прямому и ответвлен- ному путям.

3.5 Расчет основных деталей крестовины

Основные размеры крестовины зависят от её конструкции, угла и марки, величины пролёта между брусьями и числа брусьев под ней.

Минимальная длина сборной крестовины с литым сердечником

Крестовина состоит из передней (усовой) n и задней (хвостовой) q частей, которые называются вылетами крестовины. Минимальная длина переднего вылета крестовины n определяется из условия постановки первого болта в переднем стыке крестовины при двухголовых накладках:

где B – ширина подошвы;

bг – ширина головки рельса;

2ν- расстояние между подошвами усовиков криставины в месте установки первого болта в преднем стыке крестовины, принимается из условиясвободной постановки болта и зависит от длины болта и величины зазоров;

lн - длина накладки;

х1 – расстояние от торцов накладки до оси первого болтового

отверстия;

δ – стыковой зазор (8 мм).

Конструктивные значения крестовины

Минимальная длина цельнолитой крестовины

Длина переднего вылета крестовины п определяется условием расположения накладок и постановки болтов в переднем стыке крестовины. Накладки не должны заходить за первый изгиб усовиков, т. е. за горло крестовины.

При соблюдении указанного условия длина переднего вылета крестовины определяется следующей зависимостью:

2

где λ - расстояние от точки изгиба усовика до начала накладки, при- нимаемое равным 100 мм

tг - ширина желоба в горле крестовины tг = 64 мм.

Длина заднего вылета крестовины

Длина заднего вылета крестовины определяется примыканием двух рельсов к торцу сердечника крестовины.

где ∆ – зазор между подошвами рельсов, примыкающих к сердечнику

(5 мм);

B – ширина подошвы рельса; b – iширина головки рельса;

Практическая длина крестовины

Практическая длина крестовины определяется по условию рациональ- ного распределения брусьев под ней и конструктивного оформления всего узла.

Проекция переднего вылета крестовины на биссектрису крестовинного угла определяется зависимостью:

Определим практическую длину крестовины, из условия исходя из условия рационального расположения брусьев под ней. Передний и задний стыки имеют конструкцию «стык на весу». Первые брусья от

c

переднего и заднего стыка крестовины находятся на расстоянии 2 . Наибольший удар в крестовину приходится при переходе колёс с усовика на сердечник, на некотором расстоянии, составляющем около 110 мм. Расположим это сечение в середине пролёта. Тогда протяженность раскладки брусьев под усовой частью крестовины:

При принятом расстоянии между осями брусьев аб, число их на этом участке будет:

причем результат округляется до большей целой величины.

После раскладки целого числа брусьев рассчитаем фактическую проекцию переднего вылета крестовины:

Следовательно, практическая длина усовой части крестовины будет равна:

3.6 Определение теоретической и практической длины стрелочного перевода

Определение теоретической длины стрелочного перевода

Теоретической длиной LT обыкновенного одиночного стрелочного пе- ревода называется расстояние, измеренное по направлению основного пути от острия остряка до математического центра крестовины.

где LТ- теоретическая длина перевода;

l0' -проекция остряка на рамный рельс; α- угол крестовины; βП- полный стрелочный угол;

d-прямая вставка перед крестовиной

Определение практической длины стрелочного перевода

Расстояние от оси зазора в переднем стыке рамного рельса до оси зазора в заднем стыке крестовины – это практическая длина перевода (Рисунок2.9).

где LП- практическая длина перевода; m1-передний вылет рамного рельса; LТ- теоретическая длина перевода; q- задний вылет крестовины; δ-величина стыкового зазора.