Вопрос 22. Относительные показатели вариации. Относительные показатели вариации включают:
Коэффициент
осцилляции 
Относительное
линейное отклонение (линейный коэффициент
варианции)
Коэффициент
вариации (относительное отклонение)
Сравнение
вариации нескольких совокупностей по
одному и тому же признаку, а тем более
по различным признакам с помощью
абсолютных показателей не представляется
возможным. В этих случаях для сравнительной
оценки степени различия строят
относительные показатели вариации. Они
вычисляются как отношения абсолютных
показателей вариации к средней:
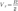Р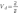
Относительное линейное отклонениеКоэффициент
вариации
ассчитываются
и другие относительные характеристики.
Например, для оценки вариации в случае
асимметрического распределения
вычисляют отношение среднего линейного
отклонения к медиан
,так
как благодаря свойству медианы сумма
абсолютных отклонений признака от ее
величины всегда меньше, чем от любой
другой.В качестве относительной меры
рассеивания, оценивающей вариацию
центральной части совокупности,
вычисляют относительное квартильное
отклонени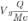е
,
где
—
средний квартиль полусуммы разности
третьего (или верхнего) квартиля (
)
и первого (или нижнего) квартиля (
).
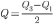.На
практике чаще всего вычисляют коэффициент
вариации. Нижней границей этого
показателя является нуль, верхнего
предела он не имеет, однако известно,
что с увеличением вариации признака
увеличивается и его значение. Коэффициент
вариации является в известном смысле
критерием однородности совокупности
(в случае нормального распределения).
23)Общая,внутригрупповая и межгрупповая дисперсия
|
Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия. |
|
Внутригрупповая дисперсия характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Такая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы X от средней арифметической группы и может быть вычислена как простая дисперсия или как взвешенная дисперсия. |
|
Таким образом, внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле: |
|
|
|
где хi — групповая средняя; ni — число единиц в группе. |
|
Например, внутригрупповые дисперсии, которые надо определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию). |
|
Средняя из внутри групповых дисперсий отражает случайную вариацию, т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле: |
|
|
|
Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле: |
|
|
|
|
