4.2. Вычисление типовых пределов

Приводятся типовые пределы с неопределенностями и некоторые способы их вычисления.

Неопределенности ,, , , содержащие алгебраические выражения.

Неопределенности ипреобразованиями переводятся вили. Последние разрешаются единым подходом: необходимо выделить в числителе и знаменателе тот множитель, который дает неопределенность и его сократить. Иногда выделение такого множителя достаточно «головоломное».

Пример 1. .

Пример 2. ==.

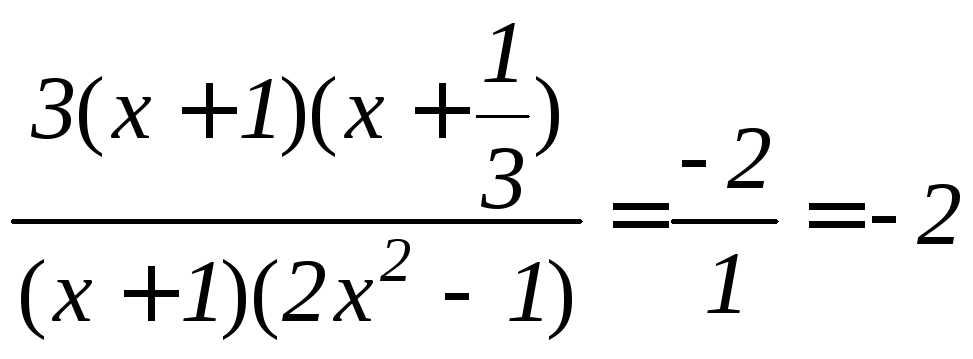Пример 3.

.

Пример 4. .

Дающий неопределенность множитель (х-1) в знаменателе выделить легко, в числителе – труднее. Нужно весь предел умножить и разделить на сопряженный числитель, т.е на .

Пример 5. .

Нетрудно догадаться, что неопределенность дает множитель (х - 1), но выделить его непросто. Нужно всё выражение умножить и разделить и на сопряженный числитель и на сопряженный знаменатель.

Пример 6. .

Обычное выделение множителя х, дающего неопределенность, не приводит к решению, т.к. опять получается неопределенность. Решение кроется в устранении радикалов любым способом, например, самым простым – заменой переменной, с дальнейшим выделением и сокращением множителя, дающего неопределенность.

.

Пример 7. .

Пример 8. .

Пример 9.

.

Пример 10. , здесь несколько видов неопределенностей, которые устраняются последовательно, аналогично арифметическим действиям=

Пример 11. , для перевода этой неопределенности внеобходимо разделить и умножить на сопряженное выражение=

Пример 12. 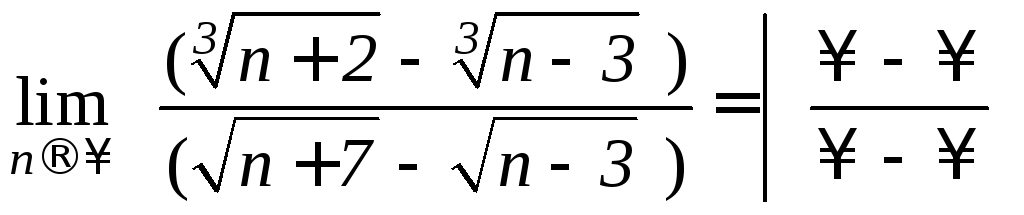, для устранения неопределенности вида () в числителе нужно все выражение умножить и разделить на неполный квадрат суммы , а в знаменателе - нужно все выражение умножить и разделить на сопряженный знаменатель.

.

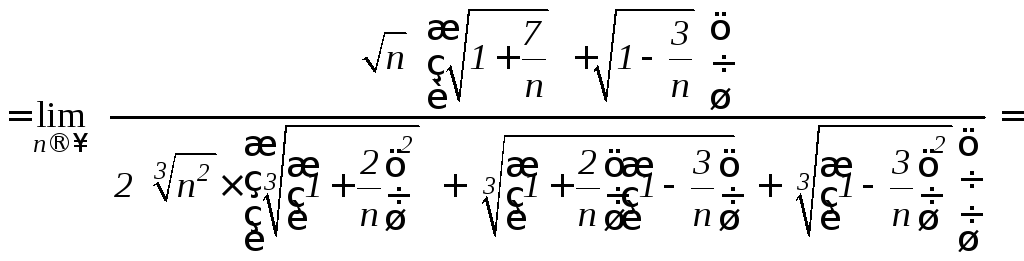
Разрешение неопределенности .

В конечном счете, эта неопределенность сводится ко 2^му замечательному пределу:

- любые непрерывные функции от х.

Иногда полезно воспользоваться 7^м свойством пределов:

.

Вот типичный пример, когда и- алгебраические выражения.

Пример.

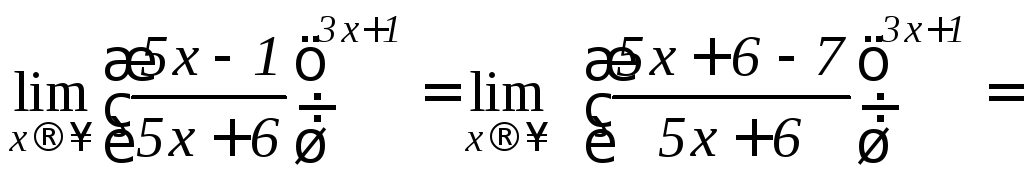
Разрешение неопределенностей с помощью важных пределов.

Общий подход: неопределенность , выраженная известными трансцендентными функциями, с помощью 1, 3, 4, 5 важных пределов преобразуется в неопределенность, выраженную алгебраическими функциями, которая разрешается сокращением в числителе и знаменателе множителя, дающего эту неопределенность.

Пример 1.

.

Пример 2. Эквивалентные замены тригонометрических функций на алгебраические производить нельзя, т.к сам аргументх не является бесконечно малой. Нужно перейти к новой переменной, которая была бы бесконечно малой и далее действовать по известному плану:

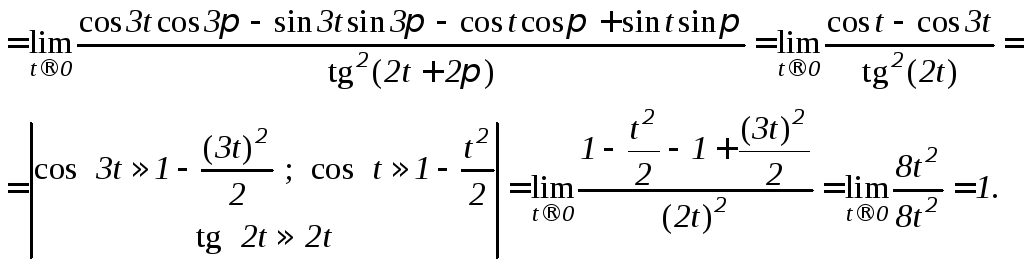
Пример 3. .

Пример 4.

.

Пример 5. непосредственный переход к новой переменной t= x - 2, с последующей заменой эквивалентных бесконечно малых приведет опять к неопределенности . Нужно предварительно «разрушить» скрытый ноль в числителе с помощью сопряженного выражения.

Пример 6.

Пример 7.