Свойства пределов

Если существуют конечные пределы то:

1. C=C

2. =C

3. =

4. =

5. =;

6. =, где- непрерывная в ()a функция. Тогда предел и функцию можно менять местами.

7. =

Если А и В являются нулями или бесконечностями, то существуют следующие виды неопределенностей: ,,,,.

Их неопределенность заключается в том, что пределы этих выражений могут быть любым числом или бесконечностью. Это зависит от интенсивности стремления каждой из бесконечно-малых к нулю и каждой из бесконечно-большой к бесконечности. Раскрытие (устранение) неопределенностей, а значит и вычисление таких пределов и составляет основное содержание индивидуальных заданий.

Свойства бесконечно-малых и бесконечно-больших

Если С; lim=lim=lim=0, то

1. ;.

2. ; ;.

3. ;или;,.

4. ;.

Важные пределы

1. .Первый замечательный предел.

На основе этого предела существуют следующие эквивалентные бесконечно-малые:

При х0 ,

или .

2. , а также.Второй замечательный предел .

3. . При

Если , то. При.

4. , при .

Если :. При.

5. 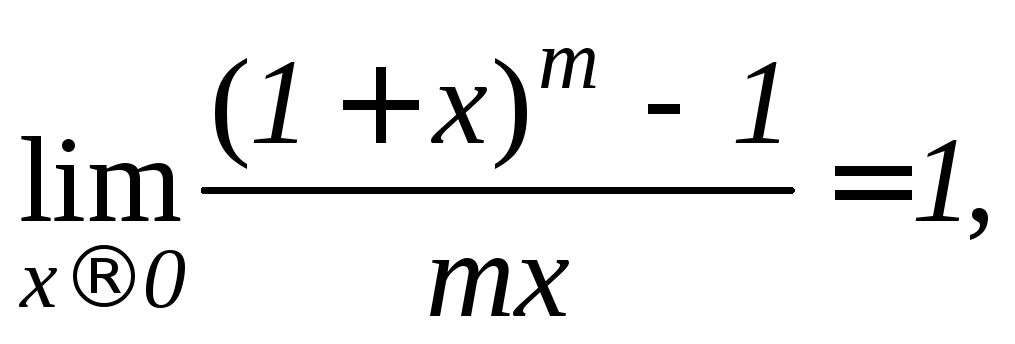пригдеm 0 – любое.

На основе 1,3,4,5 пределов можно записать общую формулу эквивалентных преобразований : х0

На рис. 4.3. приводится геометрическая интерпретация преобразования эквивалентных бесконечно малых на основе перечисленных пределов в окрестностях нуля.

y y y

у=x y=tg(x) y=argsinx

у=sinx у=х

х x x

у=х

y у y

y=x y=ln(1+x)

y=argtg x y=cos x

x

x х

y=x

y=

y y

y=x y

y=x y=x

х -1 -1 1

-1 x x

-1 -1

y=

Рис. 4.3.

Следует подчеркнуть: в окрестностях нуля трансцендентные функции sin x , tg x , arcsin x, arctg x , ln x, exp x, а также двучлен в степени m можно заменить на линейную функцию, а x на квадратичную функцию. Это обстоятельство имеет место, если аргумент х простой.

Если аргумент функции сложный, т.е в свою очередь является функцией, то рассмотренные ранее эквивалентные замены справедливы, но при условии стремления этого сложного аргумента к нулю, а сама замена должна быть соответствующей.

Так, если u=u(x), то , приu0; е^u u+1, при u0 и т.д. Пример: х,