5. Пределы
5.1 Краткие сведения из теории
Основное определение предела функции:
Число А
называется пределом
функции
при
стремящимся к
,
если для любого малого
0
существует такое малое δ0,
что неравенство 
наступает, как только наступает 
.
Обозначается:
.
Очень удобным для
понимания этого определения является
определение предела функции «на языке
окрестностей»: точка А
называется пределом функции у=
в точке a
( т.е.
), если по любойε-окрестности
()А
найдется δ-окрестность
()
такая, что для любогох,
принадлежащего δ-окрестности
()
(
),
соответствующее значение функцииу=
попадает в ε-окрестность
()А.
Оба эти равноценные определения иллюстрируются на рис. 4.1
y
у=
f(x)
А+ε
А
А-ε
а- а а+ x
Рис. 4.1
Эти определения
охватывают все возможные ситуации,
когда А
и
конечны, равны 0 или бесконечны (одно
их них или оба). Для вариантовА=∞
и
=∞
соответствующие неравенства выглядят
так:
>М;
>N,
где М>0,
N>0
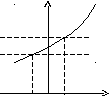
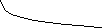
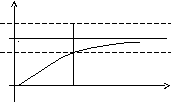
– сколь угодно большие. На рис. 4.2
приводится геометрическая «трактовка»
остальных восьми определений пределов
функции без самих определений.
y
y
M
ε
- ε
y
y
у= f(x)
ε у= f(x) A+ ε
A
- δ δ x A- ε
- ε
- δ 0 δ х
y
y
M
у= f(x)
у= f(x)
ε
x
-
δ
δ
x -ε N
y
y
A+ε
A M у= f(x)
A-ε y=f(x)
N х N x
Рис.4.2