
- •10. Функции нескольких переменных
- •10.1. Понятие функции нескольких переменных, предел и непрерывность функции нескольких переменных
- •10.2. Частные производные
- •10.3. Дифференциал функции нескольких переменных
- •10.4. Экстремум функции нескольких переменных
- •10.5. Условный экстремум
- •10.6. Наибольшее и наименьшее значения функции в замкнутой области
- •10.7. Метод наименьших квадратов
10.5. Условный экстремум
Рассмотрим задачу, специфическую для функций нескольких переменных, когда ее экстремум ищется не на всей области определения, а на множестве, удовлетворяющем некоторым дополнительным условиям (условиям связи). Такие экстремумы называются условными.
Рассмотрим общую постановку задачи нахождения условного экстремума. Пусть задана функция m+n переменных
![]() ,
(10.5)
,
(10.5)
для которой нужно найти условный экстремум при наличии m условий связи:
 (10.6)
(10.6)
Будем говорить, что функция (10.5) имеет условный экстремум при наличии связей (10.6) в точке M0, координаты которой удовлетворяют условиям связи, если ее значение в этой точке является наибольшим или наименьшим по сравнению со значениями функции в точках некоторой окрестности точки M0, координаты которых удовлетворяют условиям связи.
П
 Рис.
10.3.
Рис.
10.3.![]() при условии, чтоx
и y
связаны уравнением x+y–1=0.
при условии, чтоx
и y
связаны уравнением x+y–1=0.
Решение.
Из уравнения связи следует, что y=x–1
и
![]() .
Таким образом, при выполнении условия
связи исходная функция становится
функцией одной переменной. Ее экстремум
находится элементарно: приравниваем
нулю ее производную, получим2x–1=0,
откуда x=1/2.
В этой точке рассматриваемая функция,
очевидно, имеет минимум. Значению x=1/2
, согласно уравнению связи, соответствует
y=1/2
. Следовательно, в точке
.
Таким образом, при выполнении условия
связи исходная функция становится
функцией одной переменной. Ее экстремум
находится элементарно: приравниваем
нулю ее производную, получим2x–1=0,
откуда x=1/2.
В этой точке рассматриваемая функция,
очевидно, имеет минимум. Значению x=1/2
, согласно уравнению связи, соответствует
y=1/2
. Следовательно, в точке
 исходная функция достигает минимума
относительно уравнения связи. Геометрически
это означает, что точка параболоида
исходная функция достигает минимума
относительно уравнения связи. Геометрически
это означает, что точка параболоида![]() ,
находящаяся над точкой
,
находящаяся над точкой ,
является самой низкой из всех его
точек, лежащих над прямойx+y–1=0
(рис. 10.3). Этот пример показывает, что
точка, в которой функция достигает
условного экстремума, не является,
вообще говоря, точкой экстремума этой
функции.
,
является самой низкой из всех его
точек, лежащих над прямойx+y–1=0
(рис. 10.3). Этот пример показывает, что
точка, в которой функция достигает
условного экстремума, не является,
вообще говоря, точкой экстремума этой
функции.
Однако на практике решение системы (10.6) оказывается в явном виде невозможным или весьма затруднительным, поэтому для отыскания точек условного экстремума чаще используют метод неопределенных множителей Лагранжа , который основан на следующей теореме:
Теорема. Пусть точка M0 является точкой условного экстремума функции u=f(M) при выполнении уравнений связи (10.6). Тогда существуют такие числа 1, 2, …, m, что в точке M0 будут выполняться условия
 .
(10.7)
.
(10.7)
Функцией Лагранжа для данной функции u=f(M) называется функция
 (10.8)
(10.8)
Из теоремы следует, что если точка M0 является точкой условного экстремума функции u=f(M), то она является стационарной точкой для функции Лагранжа, т.е. должны выполняться условия:
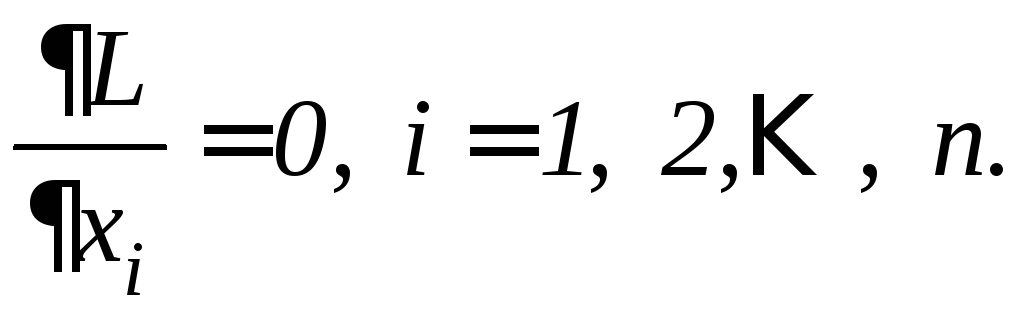 (10.9)
(10.9)
Таким образом, для отыскания точек условного экстремума следует рассмотреть систему n+m уравнений (10.6) и (10.9) относительно неизвестных x1,…,xn, 1,…,m и решить ее (если это окажется возможным), найдя x1,…,xn и по возможности исключив 1,…,m. Сформулированная теорема утверждает, что все точки условного экстремума будут находиться среди найденных таким образом точек. Вопрос о том, какие же из них фактически будут точками условного экстремума, требует дополнительного исследования.
В
случае функции двух переменных
![]() при одном уравнении связи
при одном уравнении связи![]() функция Лагранжа имеет вид
функция Лагранжа имеет вид![]() .
Система уравнений (10.6) и (10.9) будет
содержать три уравнения:
.
Система уравнений (10.6) и (10.9) будет
содержать три уравнения:
 (10.10)
(10.10)
Сформулируем
достаточное
условие
условного экстремума. Пусть
![]() и0
– решение системы (10.10),
и0
– решение системы (10.10),
 .
(10.11)
.
(10.11)
Если
![]() ,
то функция
,
то функция![]() имеет в точке
имеет в точке![]() условный максимум,
условный максимум,![]() – условный минимум.
– условный минимум.
Пример 9. Найти экстремум функции u=xy при условии, что x и y связаны уравнением 2x+3y–5=0.
Решение. Составим функцию Лагранжа
![]() .
.
Поскольку![]()
 ,
то
,
то
из
системы уравнений
 находим
находим
![]()
Таким
образом, стационарная точка
 может быть точкой условного экстремума.
может быть точкой условного экстремума.
Вычислим
в точке M
определитель
![]()
![]() ,
,
![]() .
.
 .
.
Итак,
точка
 является точкой условного максимума
для рассмотренной задачи.
является точкой условного максимума
для рассмотренной задачи.
