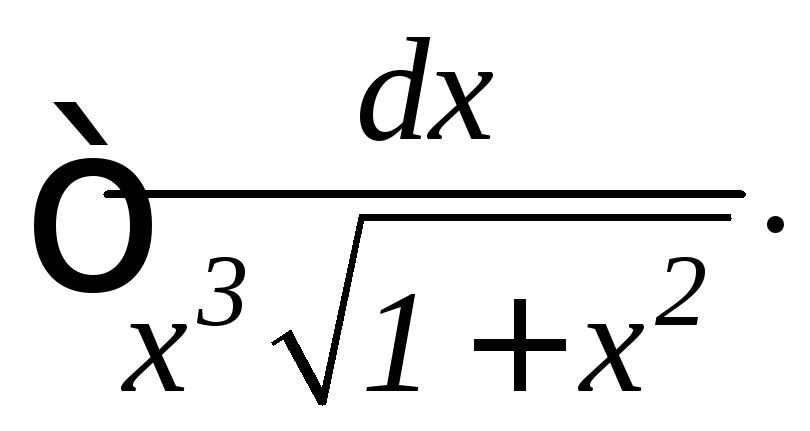8.7. Интегрирование тригонометрических функций
1. Интегралы вида
![]() гдеm иn
– целые числа.
гдеm иn
– целые числа.
Если хотя бы одно из чисел m иn – нечетное положительное, то применяют подстановкуcosx=z, приm– нечетном иsinx=z, приn– нечетном.
Найти интеграл![]()
Применяем подстановку sinx=z,cosx= dz
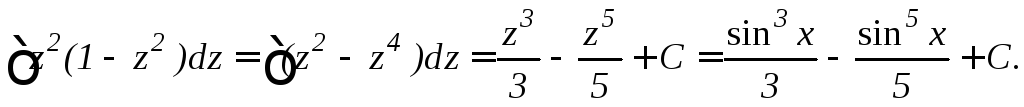
Если mиn– четные положительные, то степени понижаются с применением формул вида:
![]() и
и![]()
Найти интеграл![]()
![]()
![]()
![]()
Если m иn – четные и хотя бы один из них отрицательный, то применяют подстановкуtgx =z илиctgx=z.
Например,
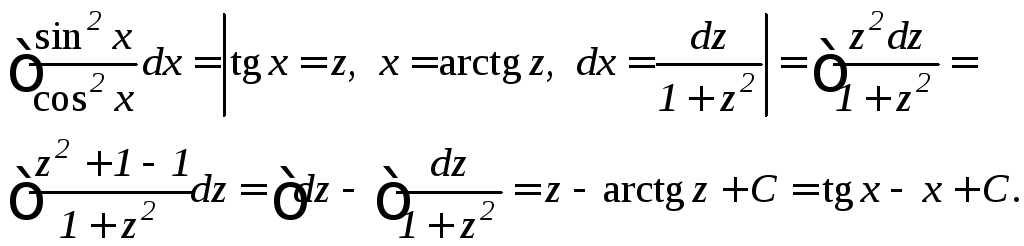
![]() 2.
Интегралы вида
2.
Интегралы вида
![]()
Для нахождения данных интегралов применяют формулы из тригонометрии
![]()
![]()
![]()
Найти интеграл:
![]()
![]()
3. Интегралы вида![]()
где R (sinx, cosx) – рациональная функция относительноsinxиcosx.
Для нахождения данных интегралов применяют подстановку:
![]() при этом
при этом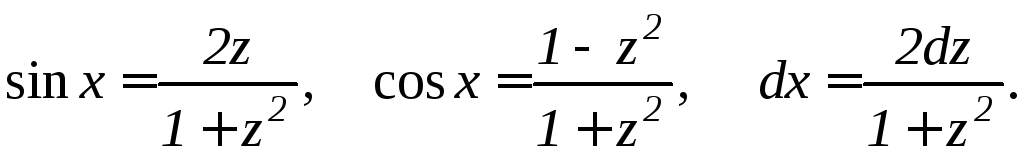
Найти интеграл![]()
Применяя указанную формулу, получим

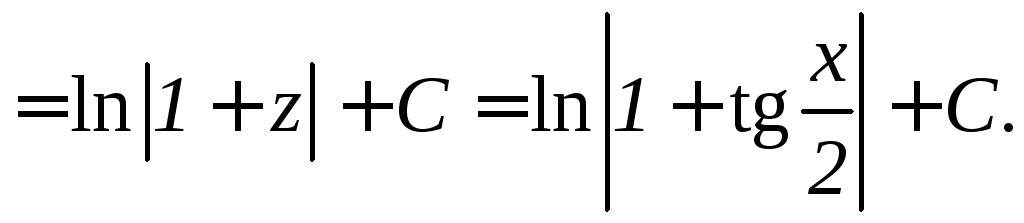
Задание 8.7.Найти интегралы:
1.
![]() 2.
2.![]()
3.
![]() 4.
4.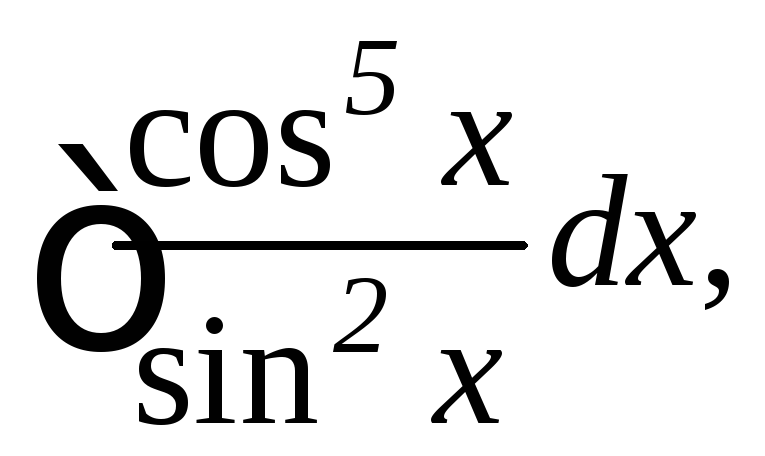
5.
 6.
6.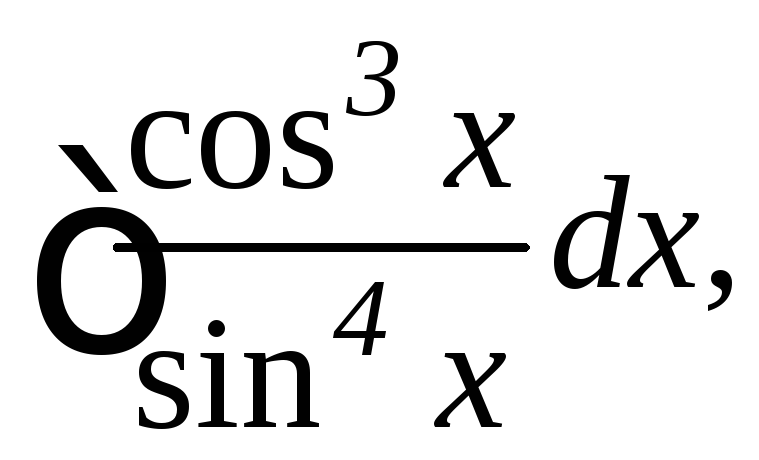
7.
![]() 8.
8.![]()
9.
![]() 10.
10.![]()
11.
![]() 12.
12.![]()
13.
![]() 14.
14.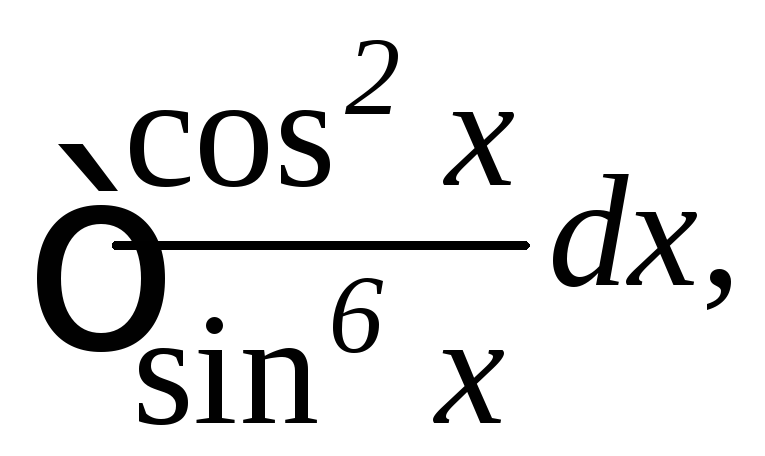
15.
![]() 16.
16.![]()
17.
![]() 18.
18.![]()
19.
![]() 20.
20.![]()
21.
![]() 22.
22.![]()
23.
![]() 24.
24.![]()
25.
![]()
8.8. Интегрирование некоторых иррациональных функций
1. Интегралы вида
![]()
![]()
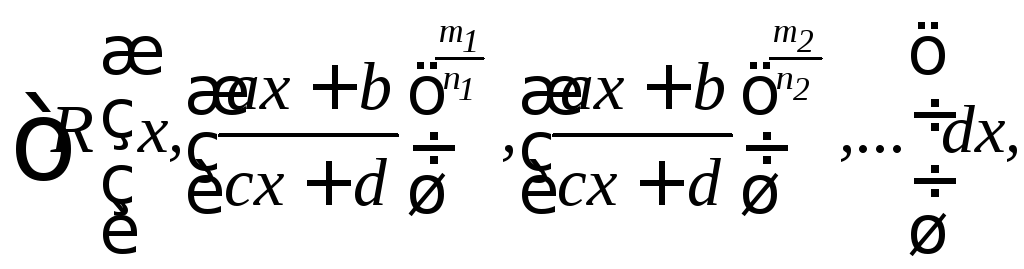 гдеR (x,
y, z,
…)– рациональная функция своих
аргументов,m1,
n1, m2,
n2,…
- целые числа, вычисляются с помощью
подстановок , соответственно
гдеR (x,
y, z,
…)– рациональная функция своих
аргументов,m1,
n1, m2,
n2,…
- целые числа, вычисляются с помощью
подстановок , соответственно
![]()
где s – общий
знаменатель дробей .
.
Пример: Найти интеграл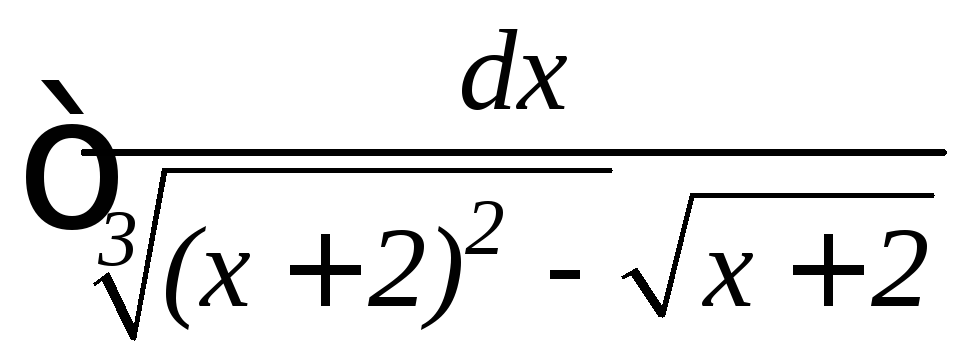 .
.
Производим подстановку x + 2 = z6, dx = 6 z5 dz.
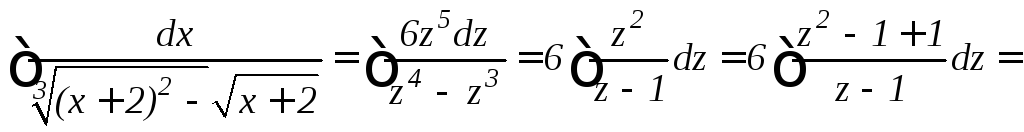
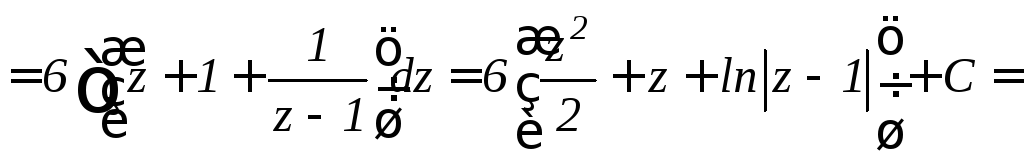
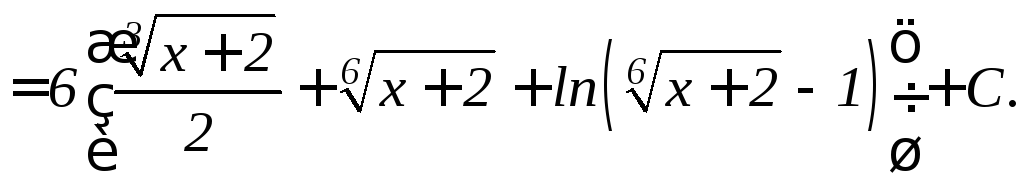
Интегралы вида
![]()
сводятся к интегралам от рациональной функции относительно sint иcost, если применить соответственно подстановки:
x = a sint или x = a cost ,
x = a tg t или x = a ctgt ,
x = a sect или x = a cosect .
Пример: Найти интеграл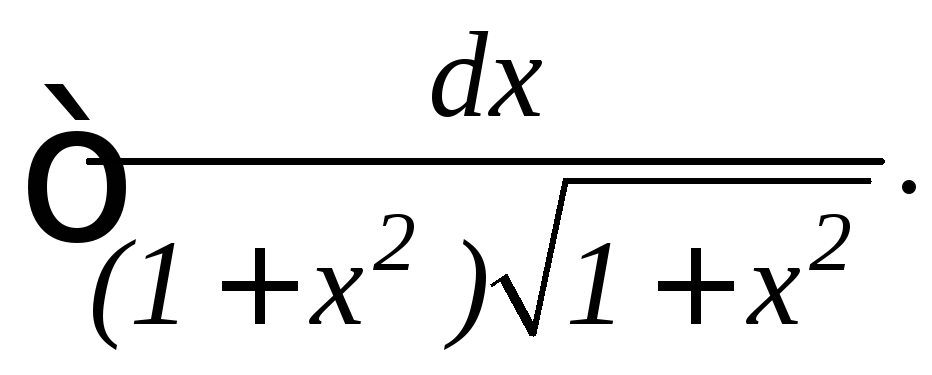
Положим x =tgt
, тогда![]()
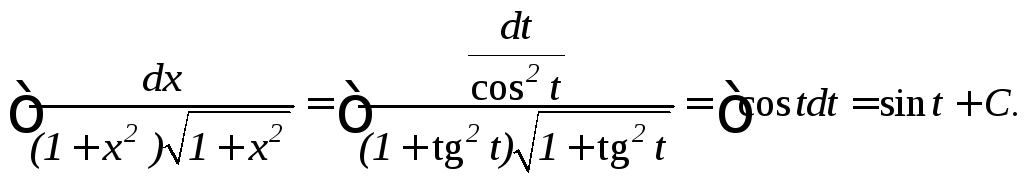
Выразим sint через заданную переменнуюx :
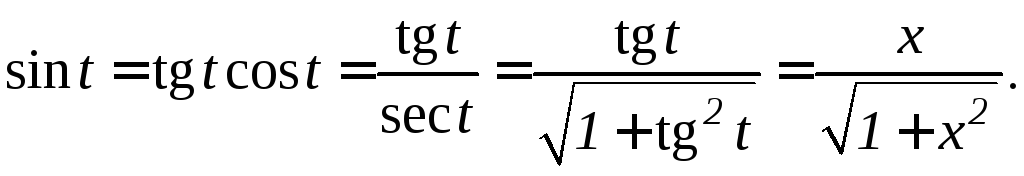
Следовательно,
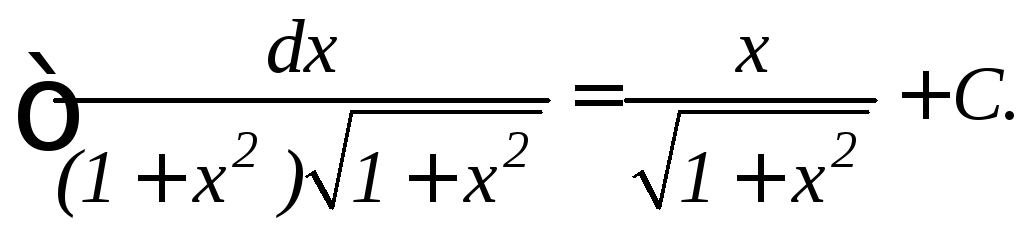
Задание 8.8.Найти интегралы:
1.
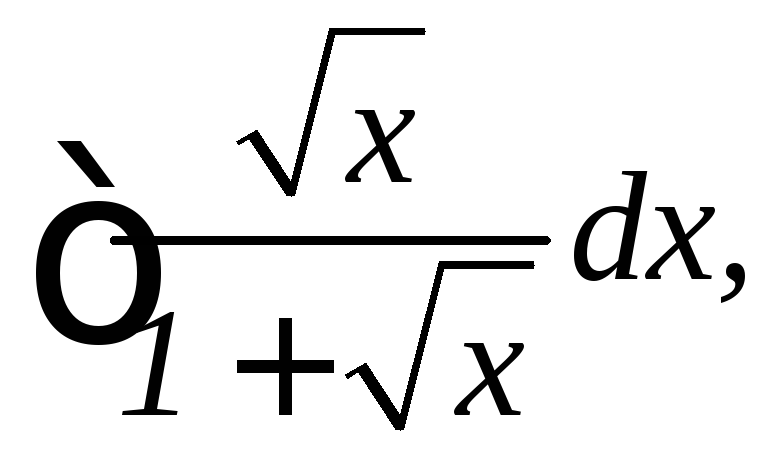 2.
2.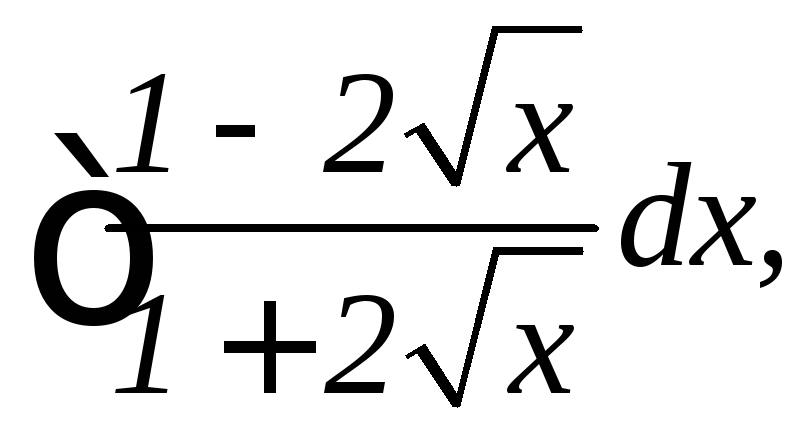
3.
 4.
4.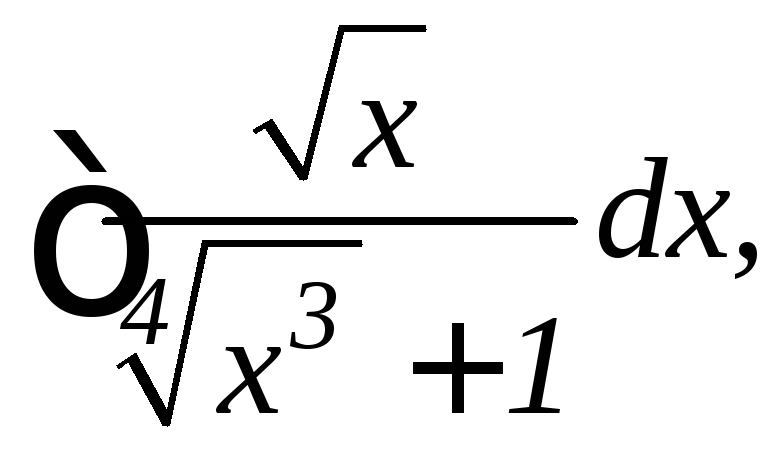
5.
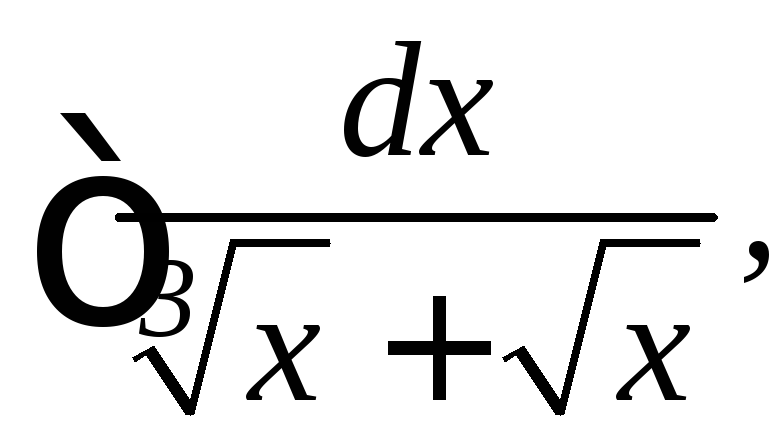 6.
6.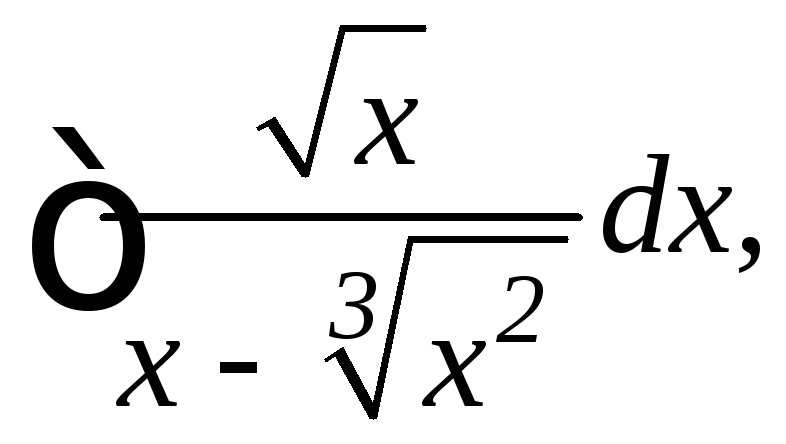
7.
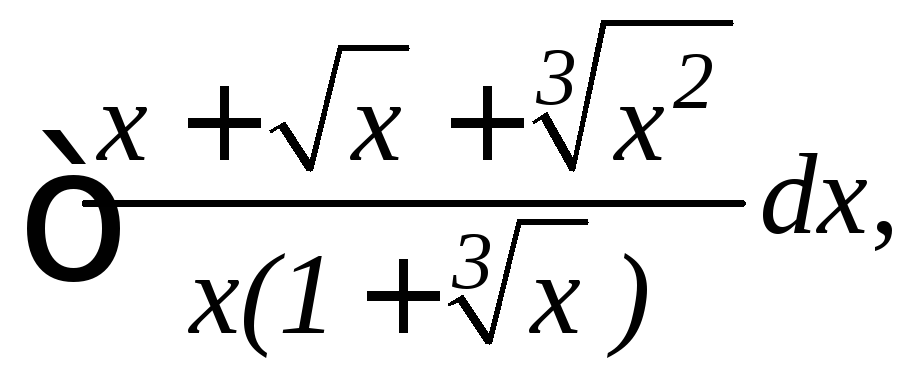 8.
8.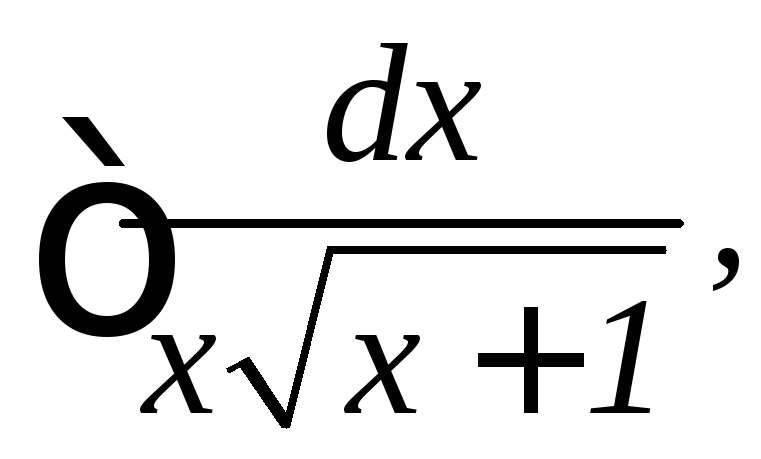
9.
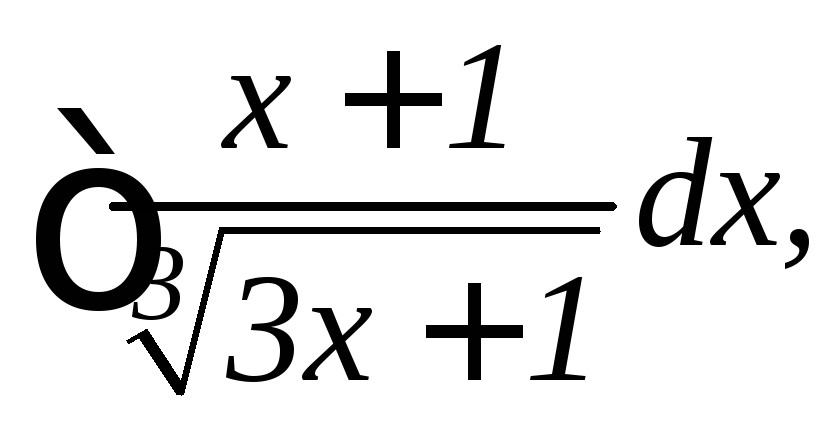 10.
10.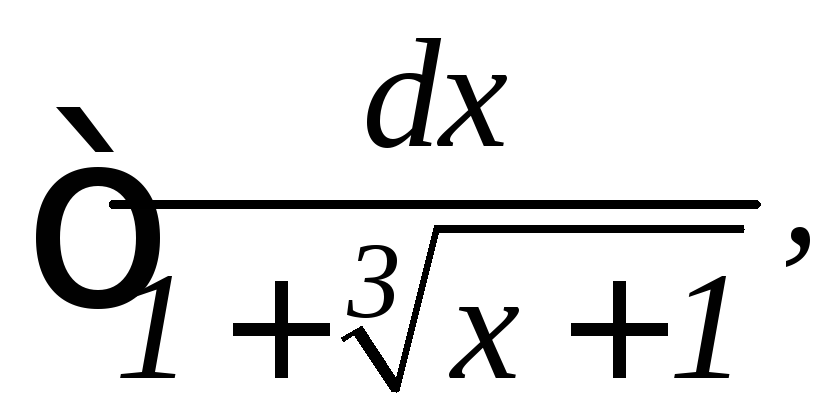
11.
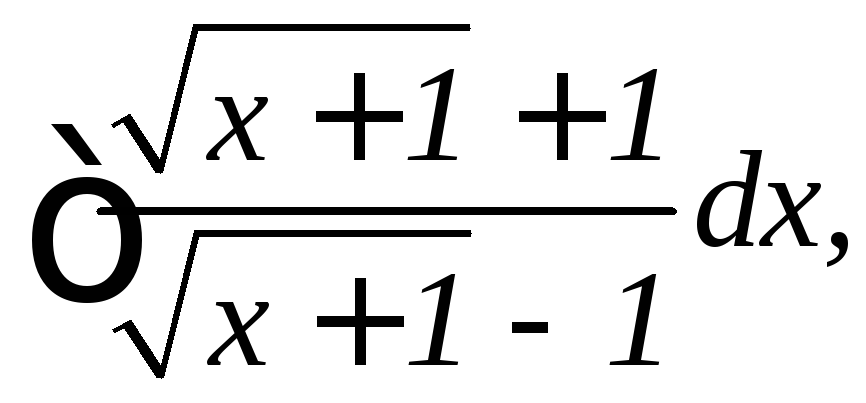 12.
12.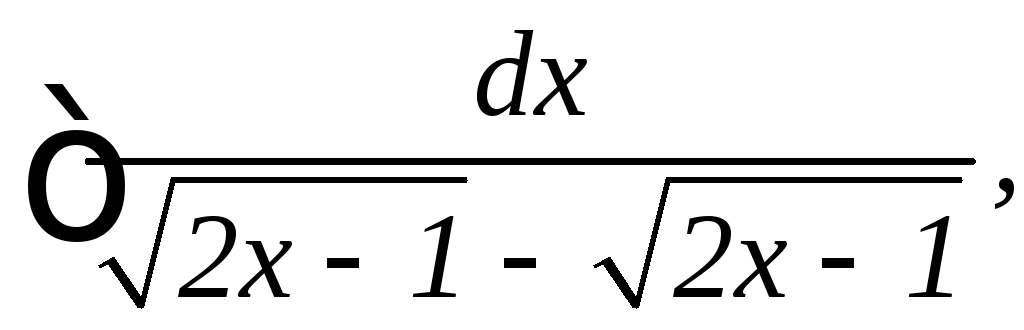
13.
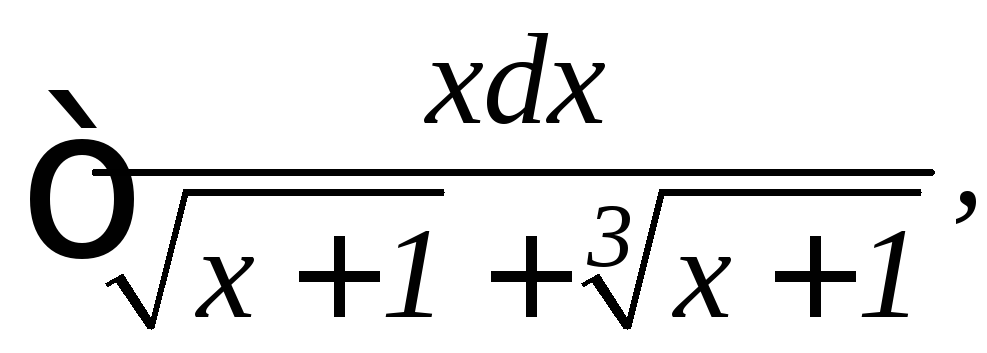 14.
14.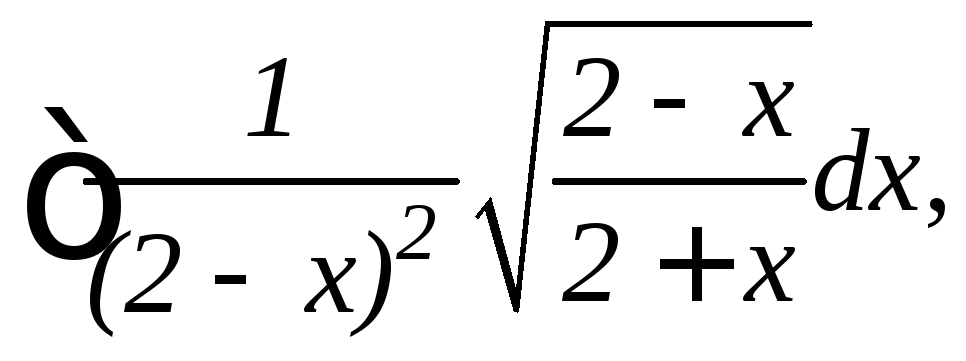
15.
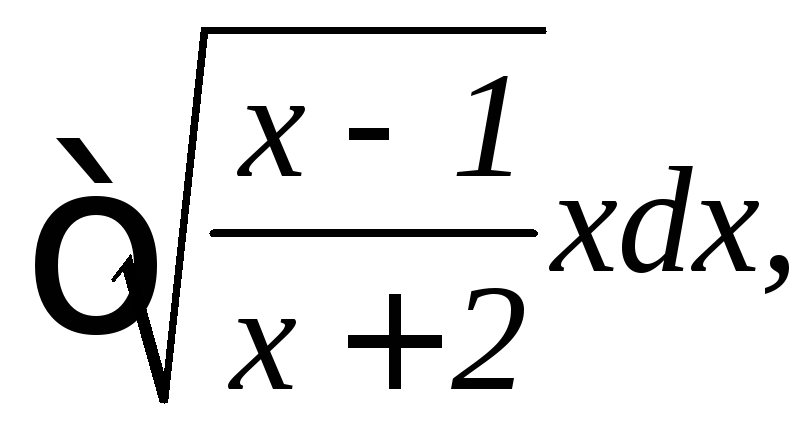 16.
16.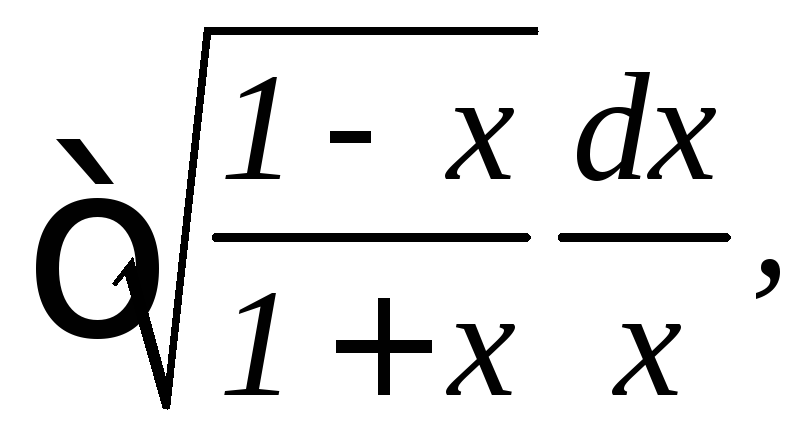
17.
![]() 18.
18.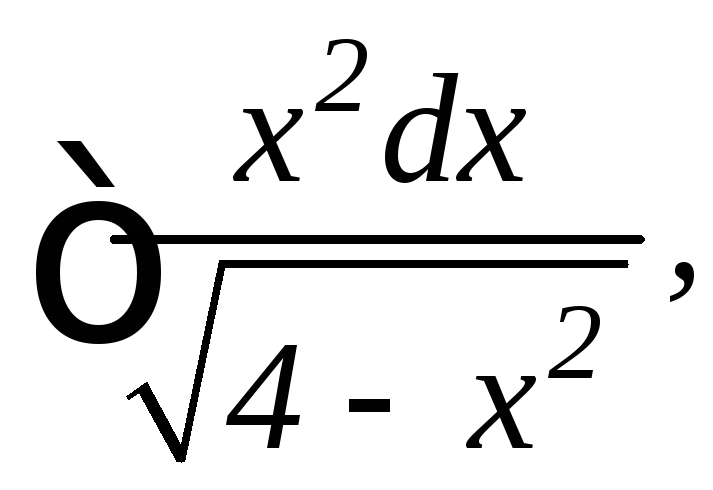
19.
![]() 20.
20.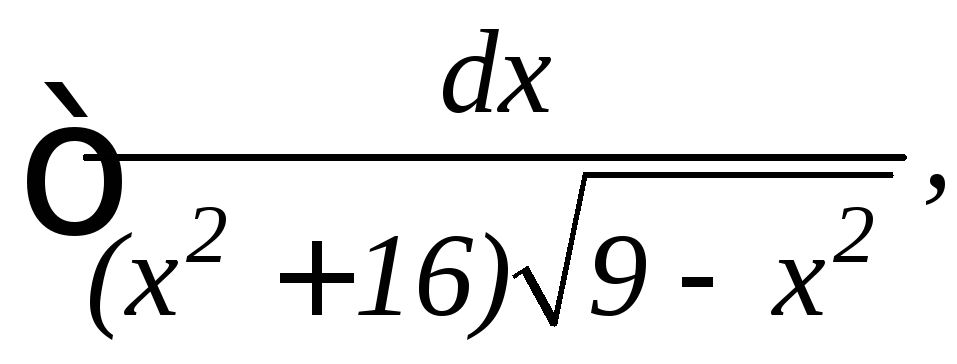
21.
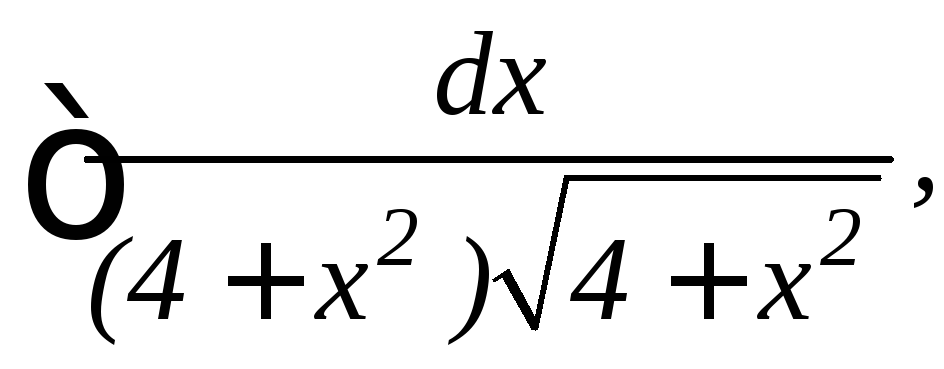 22.
22.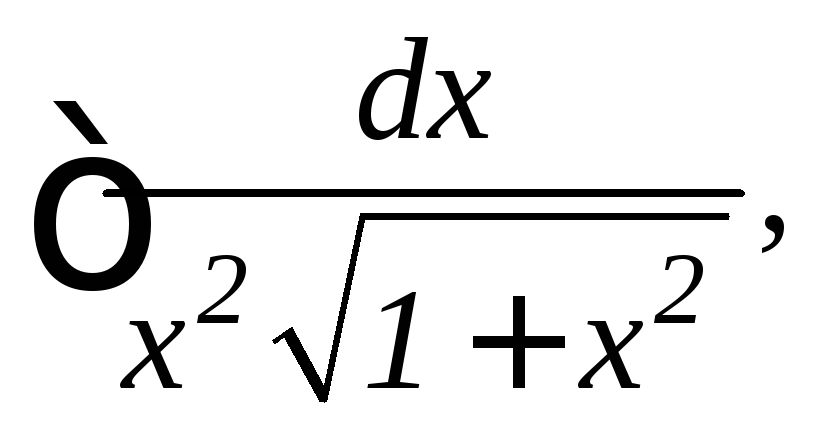
23.
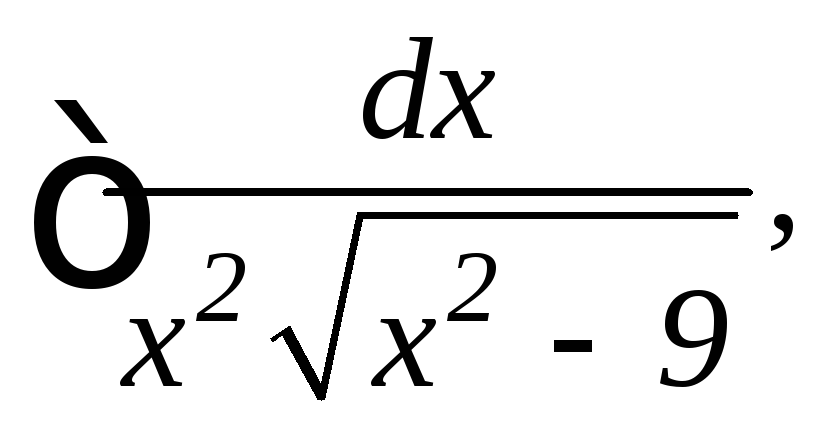 24.
24.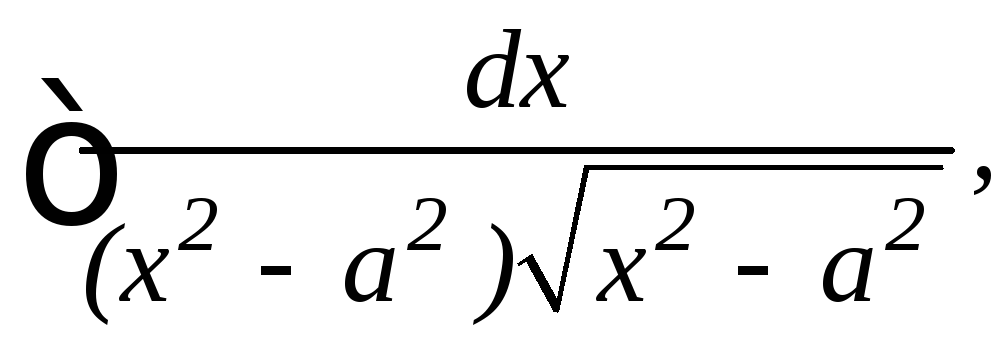
25.