
- •12. Кратные интегралы
- •12.1. Двойной интеграл
- •Решение. Непосредственное вычисление данного интеграла было бы затруднительным. Однако простая замена переменных
- •Решение. Применив формулу (12.4), перейдем к полярным координатам:
- •Решение. Область представляет собой фигуру, ограниченную слева параболой, справа прямой. Решая систему уравнений
- •Решение. Данное тело ограничено двумя параболоидами (рис. 12.9). Решая систему уравнений
- •Решение. Уравнение поверхности имеет вид , областьесть круг, ограниченный окружностью. Находим производные
- •Решение. Находим массу и статические моменты:
- •Решение. Момент инерции относительно начала координат равен
- •12.2. Тройной интеграл
- •Решение. Область проецируется на плоскостьв треугольник, ограниченный прямыми,,. По формуле (12.5) имеем
- •Решение. Данное тело ограничено сверху плоскостью , снизу – параболоидом(рис. 12.18). Объем тела находим, используя цилиндрические координаты:
- •Решение. Найдем массу рассматриваемого тела:
- •12.3. Задачи
Решение. Область проецируется на плоскостьв треугольник, ограниченный прямыми,,. По формуле (12.5) имеем

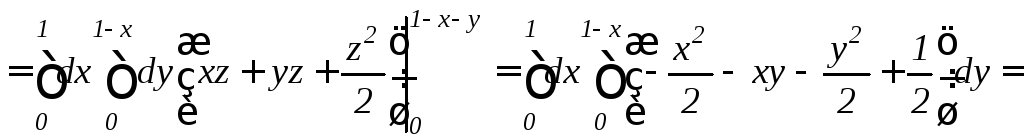

 .
.
Замена переменных в тройном интеграле производится по формуле
![]() ,
,
где
![]() - область, в которую преобразовалась
область
- область, в которую преобразовалась
область![]() при отображении
при отображении![]() ,
,![]() ,
,![]() ;
;![]() -подынтегральная
функция, преобразованная к новым
переменным
-подынтегральная
функция, преобразованная к новым
переменным
![]() ,
,![]() ,
,![]() ;
;![]() - якобиан функций
- якобиан функций![]() ,
,![]() ,
,![]() по переменным
по переменным![]() ,
,![]() ,
,![]() :
:
 .
.
В частности, при
переходе от прямоугольных координат
![]() ,
,![]() ,
,![]() кцилиндрическим
координатам
кцилиндрическим
координатам
![]() ,
,![]() ,
,![]() (рис. 12.14), связанным с
(рис. 12.14), связанным с![]() ,
,![]() ,
,![]() формулами
формулами
![]() ,
,
![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() ),
),
якобиан преобразования
![]() ,
поэтому
,
поэтому
![]() .
(12.6)
.
(12.6)
|
|
|
|
Рис. 12.14 |
Рис. 12.15 |
При переходе от
прямоугольных координат
![]() ,
,![]() ,
,![]() ксферическим
координатам
ксферическим
координатам
![]() ,
,![]() ,
,![]() (рис. 12.15), связанным с
(рис. 12.15), связанным с![]() ,
,![]() ,
,![]() формулами
формулами
![]() ,
,
![]() ,
,![]()
(![]() ,
,![]() ,
,![]() ),
),
якобиан преобразования
![]() ,
поэтому
,
поэтому
![]()
![]() .
(12.7)
.
(12.7)
Пример 11.
Вычислить тройной интеграл
 ,
где область
,
где область![]() ограничена параболоидом
ограничена параболоидом![]() и плоскостью
и плоскостью![]() (рис. 12.16).
(рис. 12.16).
Рис. 12.16
![]() проецируется на плоскость
проецируется на плоскость![]() в круг, ограниченный окружностью
в круг, ограниченный окружностью![]() (ее уравнение получается в результате
исключения
(ее уравнение получается в результате
исключения![]() из уравнений параболоида
из уравнений параболоида![]() и плоскости
и плоскости![]() ).
).
Тройной интеграл
удобнее вычислять в цилиндрических
координатах. Уравнение параболоида при
этом запишется следующим образом:
![]() ,
т.е.
,
т.е.![]() .
В области
.
В области![]() координаты
координаты![]() ,
,![]() и
и![]() изменяются так:
изменяются так:![]() ,
,![]() ,
,![]() ;
подынтегральная функция
;
подынтегральная функция![]() .
Таким образом, по формуле (12.6) находим
.
Таким образом, по формуле (12.6) находим
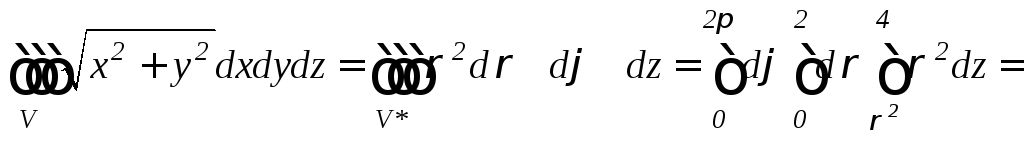
 .
.
Рис. 12.17
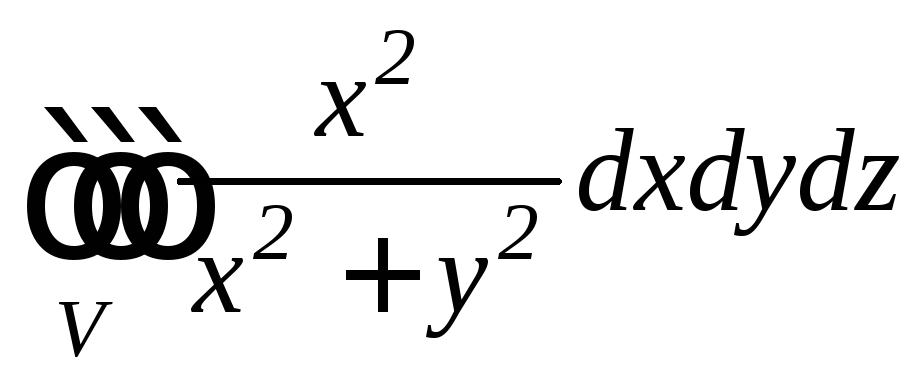 ,
где область
,
где область![]() ограничена поверхностями
ограничена поверхностями![]() ,
, .
.
Решение. Поскольку
![]() - область, ограниченная верхней полусферой
и конусом (рис. 12.17), удобно перейти к
сферическим координатам. Уравнение
полусферы при этом запишется как
- область, ограниченная верхней полусферой
и конусом (рис. 12.17), удобно перейти к
сферическим координатам. Уравнение
полусферы при этом запишется как![]() ,
а конуса -
,
а конуса -![]() .
В области
.
В области![]() координаты изменяются следующим
образом:
координаты изменяются следующим
образом:![]() ,
,![]() ,
,![]() .
Таким образом, по формуле (12.7) находим
.
Таким образом, по формуле (12.7) находим

 .
.
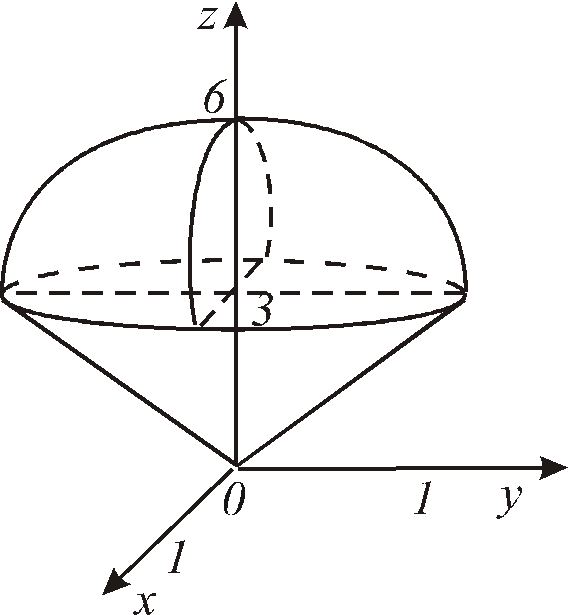
Объем тела,
занимающего область
![]() ,
определяется по формуле
,
определяется по формуле
![]() .
.
Рис. 12.18

![]() и
и![]() .
.
Решение. Данное тело ограничено сверху плоскостью , снизу – параболоидом(рис. 12.18). Объем тела находим, используя цилиндрические координаты:
![]()

 .
.
Масса тела,
занимающего область
![]() ,
вычисляется по формуле
,
вычисляется по формуле
![]() ,
,
где
![]() - плотность тела.
- плотность тела.
Статические
моменты
тела относительно координатных плоскостей
![]() ,
,![]() ,
,![]() вычисляются по формулам
вычисляются по формулам
![]() ,
,
![]() ,
,
![]() .
.
Координаты центра тяжести определяются по формулам
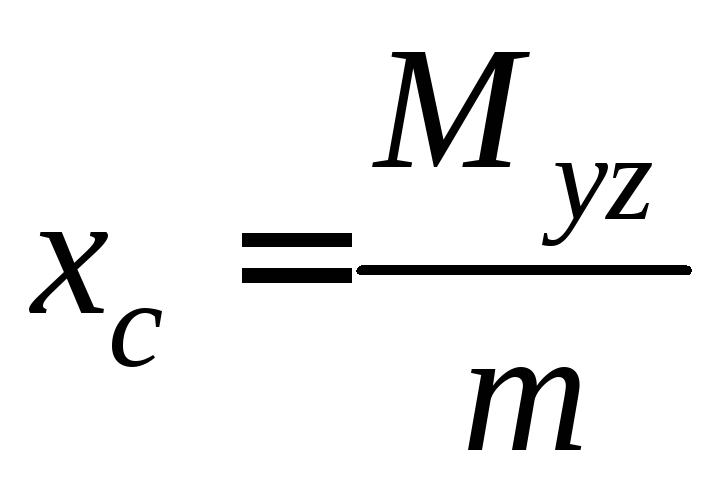 ,
,
![]() ,
, .
.
Моменты инерции
относительно координатных осей
![]() ,
,![]() ,
,![]() ;
моменты инерции относительно координатных
плоскостей
;
моменты инерции относительно координатных
плоскостей![]() ,
,![]() ,
,![]() и момент инерции относительно начала
координат вычисляются соответственно
по формулам
и момент инерции относительно начала
координат вычисляются соответственно
по формулам
 ,
,
 ,
,
 ;
;
![]() ,
,
![]() ,
,
![]() ;
;
 .
.
Рис. 12.19

![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (рис. 12.19).
(рис. 12.19).
Решение. Найдем массу рассматриваемого тела:

 .
.
Статические моменты:

 ;
;

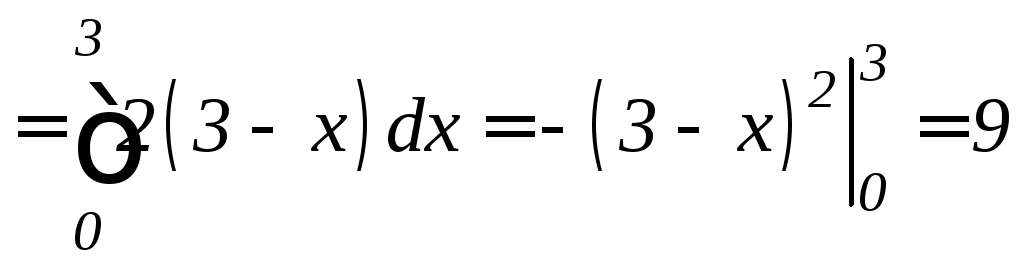 ;
;
 .
.
Тогда координаты центра тяжести:
 ,
,
![]() ,
, .
.
12.3. Задачи
Начертить области интегрирования и изменить порядок интегрирования в следующих двойных интегралах:
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
5. |
|
|
6. |
|
Вычислить двойные интегралы:
|
7. |
|
8. |
|
Вычислить двойные
интегралы по областям
![]() ,
ограниченным указанными линиями:
,
ограниченным указанными линиями:
 ,
где
,
где
 - область, ограниченная прямыми
- область, ограниченная прямыми ,
, и
и .
. ,
где
,
где
 - область, ограниченная параболами
- область, ограниченная параболами и
и .
. ,
где
,
где
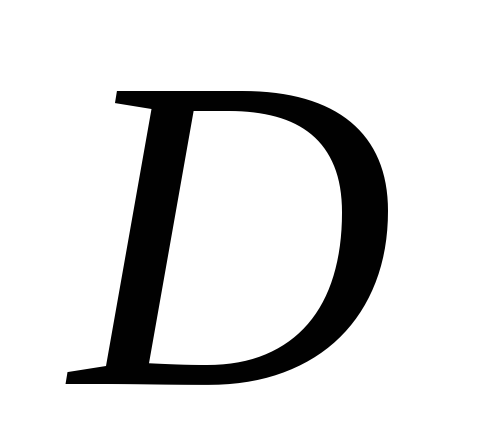 - область, ограниченная прямыми
- область, ограниченная прямыми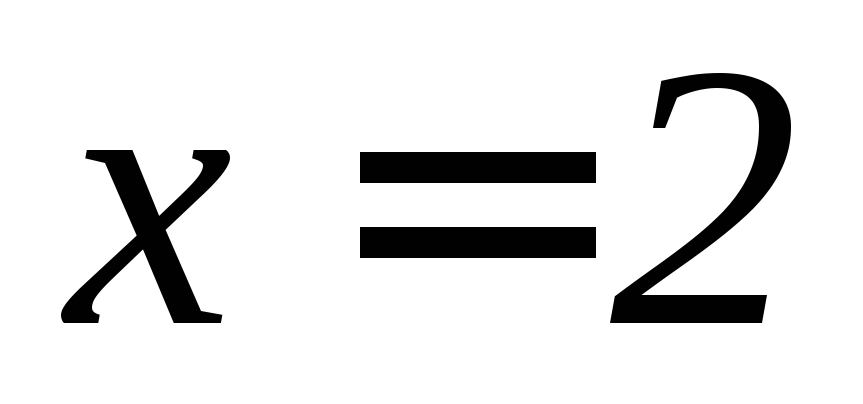 ,
, и гиперболой
и гиперболой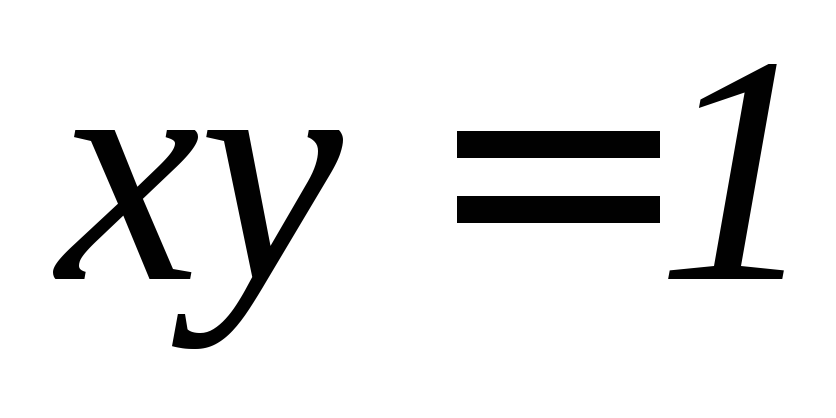 .
. ,
где
,
где
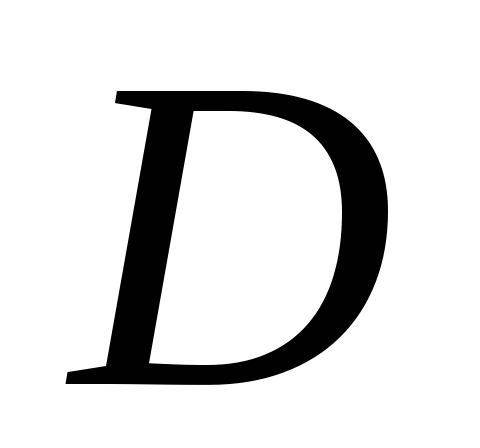 - область, ограниченная линиями
- область, ограниченная линиями ,
, ,
, .
.
Переходя к полярным координатам, вычислить двойные интегралы:
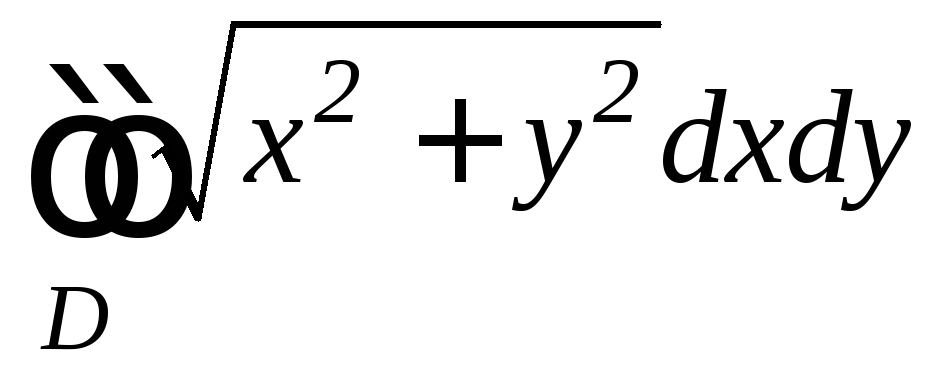 ,
где область
,
где область
 - круг
- круг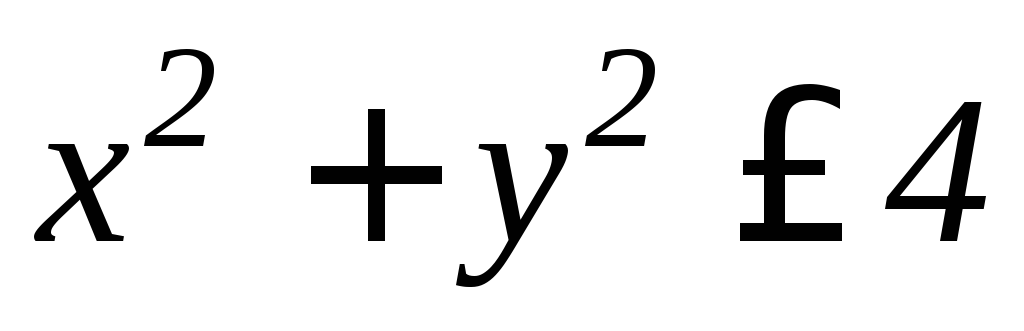 .
.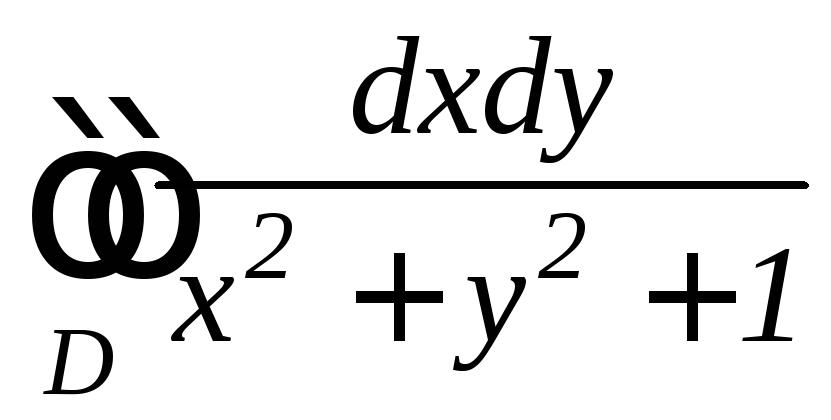 ,
где область
,
где область
 ограничена полуокружностью
ограничена полуокружностью и осью
и осью .
. ,
где область
,
где область
 ограничена линиями
ограничена линиями ,
, .
. ,
где область
,
где область
 ограничена окружностью
ограничена окружностью .
. ,
где область
,
где область
 ограничена линиями
ограничена линиями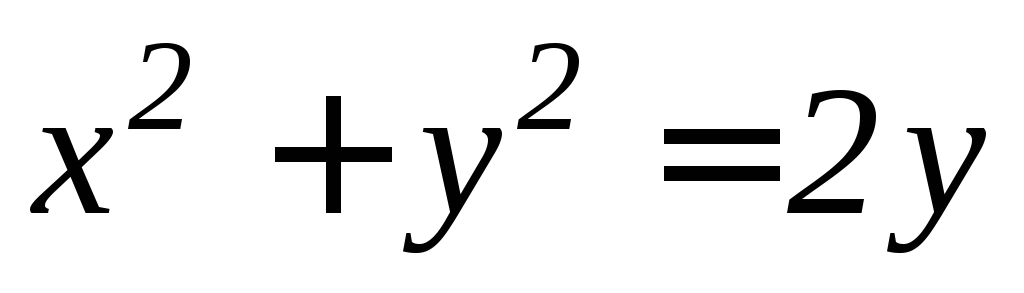 ,
, ,
, ,
,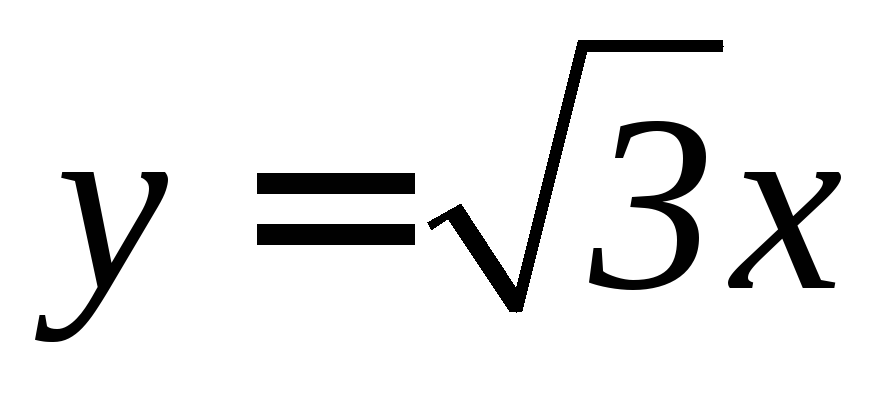 .
.Вычислить двойной интеграл
 ,
,
 .
.
Найти площади плоских фигур, ограниченных заданными линиями
|
19. |
|
|
20. |
|
 ,
,
 ,
, ,
,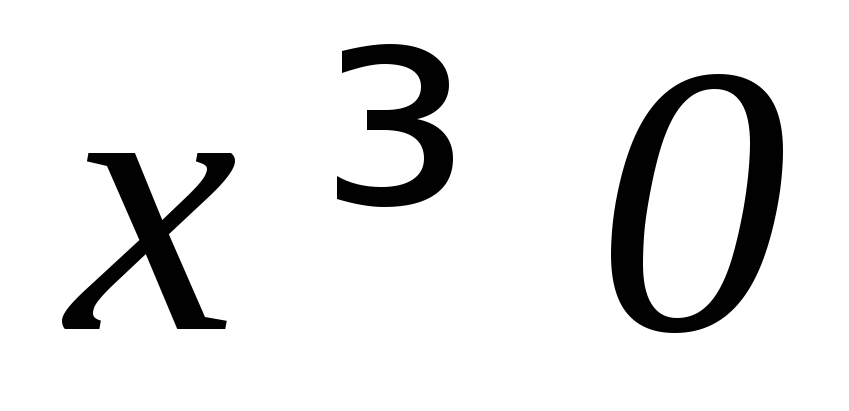 .
.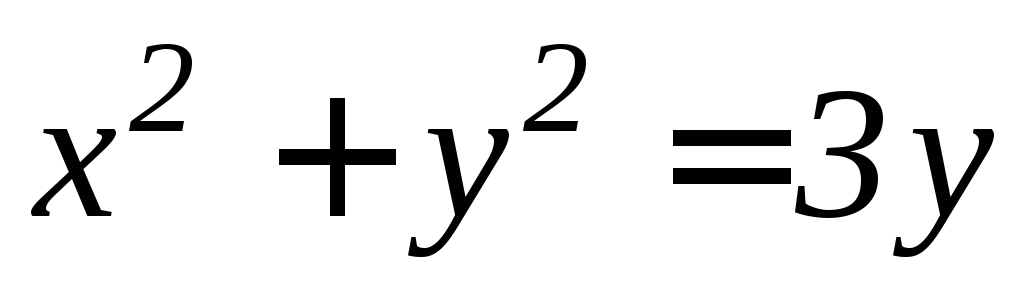 ,
,
 ,
,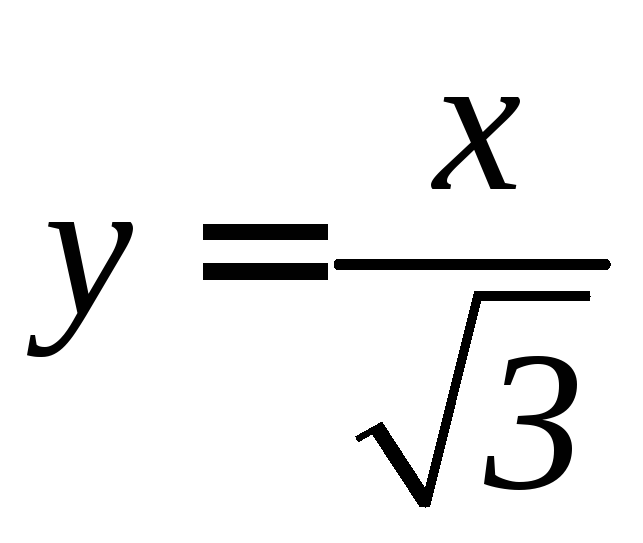 ,
, .
.
С помощью двойного интеграла найти объем тела, ограниченного заданными поверхностями:
Плоскостями координат, плоскостями
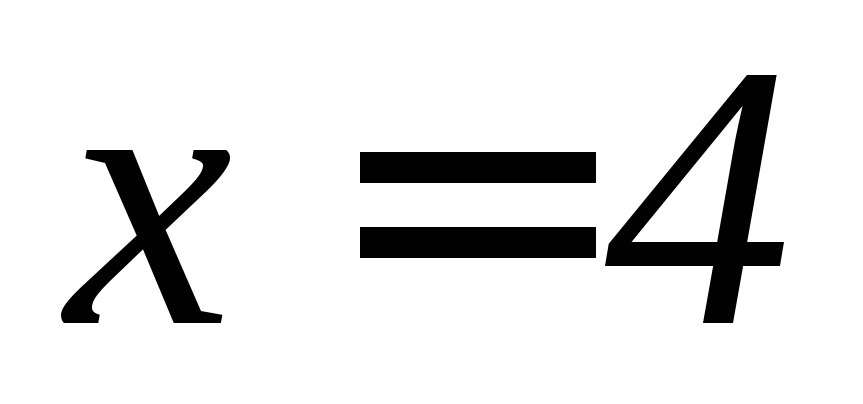 ,
, и параболоидом вращения
и параболоидом вращения .
.Цилиндром
 и плоскостями
и плоскостями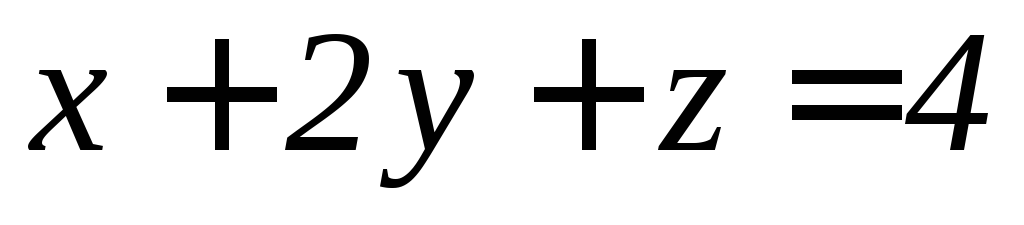 ,
, ,
, .
.Плоскостями координат, плоскостью
 и цилиндром
и цилиндром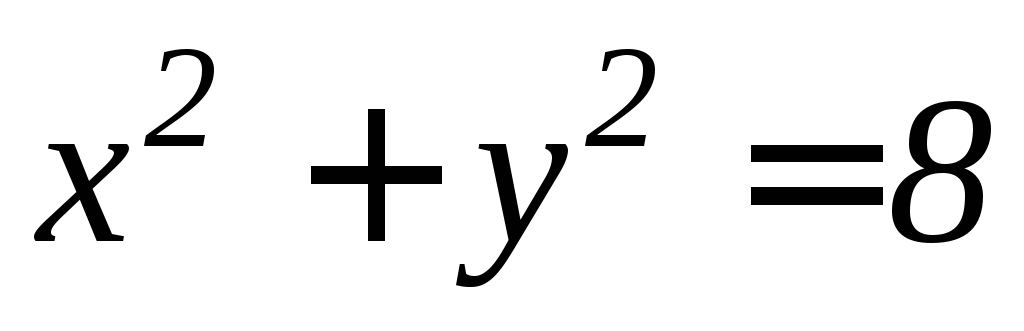 .
.Цилиндром
 ,
параболоидом
,
параболоидом и плоскостью
и плоскостью .
.
Вычислить площадь:
Части плоскости
 ,
находящейся вI
октанте (
,
находящейся вI
октанте ( ,
, ,
, ).
).Части поверхности
 ,
вырезанной цилиндром
,
вырезанной цилиндром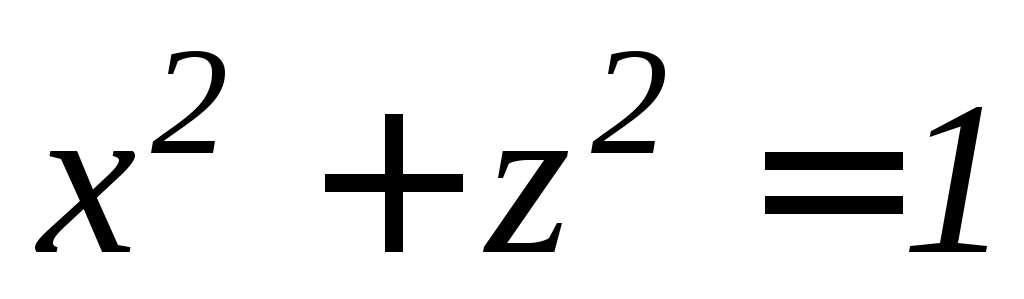 и расположенной вI
октанте.
и расположенной вI
октанте.
Найти массу плоской
пластинки с плотностью распределения
массы
![]() ,
ограниченной заданными линиями:
,
ограниченной заданными линиями:
 ,
,
 ,
, ,
, (
( ).
). ,
,
 ,
, ,
, ,
,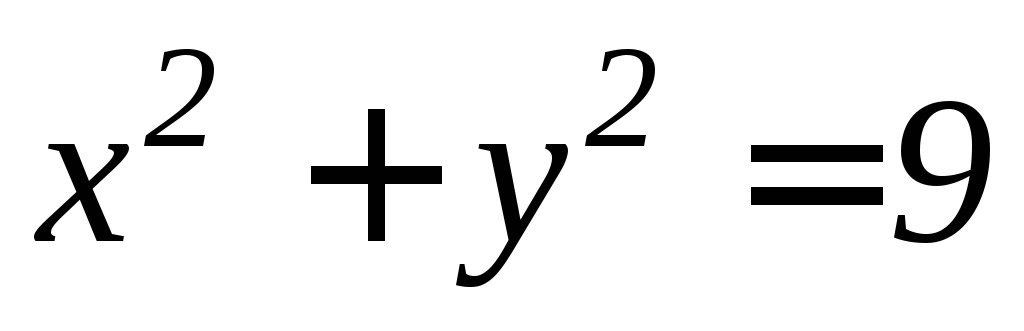 (
( ,
, ).
).
Определить центр тяжести однородной пластинки, ограниченной заданными линиями:
|
31. |
|
|
|
|
32. |
|
|
|
Вычислить моменты
инерции фигуры, ограниченной заданными
линиями, относительно осей
![]() и
и![]() :
:
|
33. |
|
|
|
|
34. |
|
|
|
Вычислить тройные
интегралы по областям
![]() ,
ограниченным указанными поверхностями:
,
ограниченным указанными поверхностями:
 ,
,
 ,
, ,
, ,
,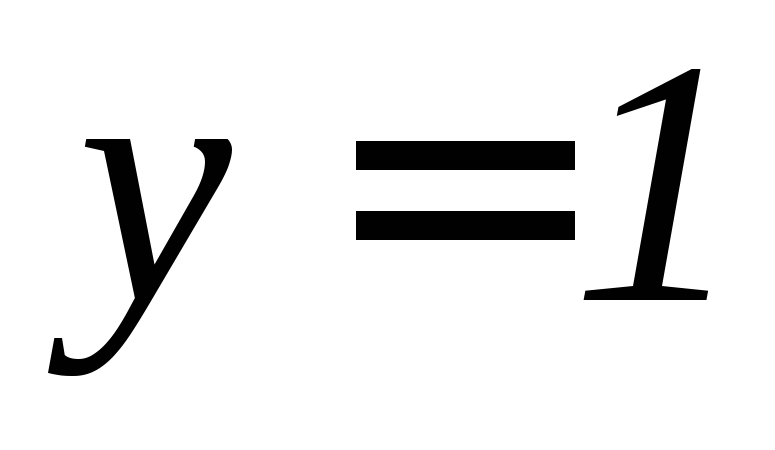 ,
, ,
, .
.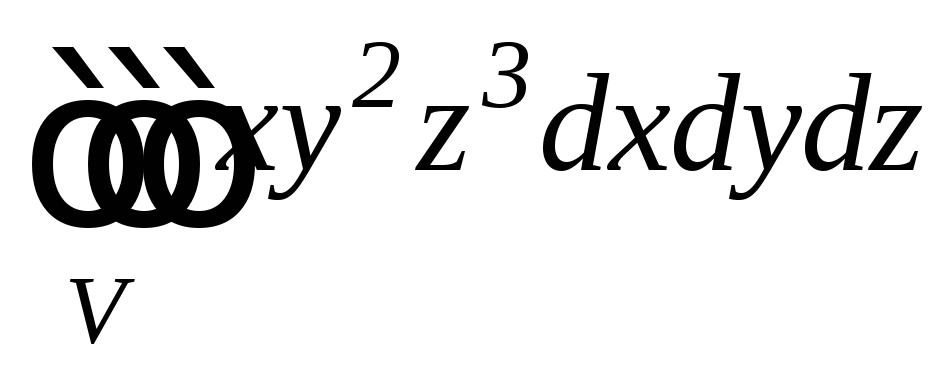 ,
,
 ,
, ,
, ,
, .
. ,
,
 ,
, ,
,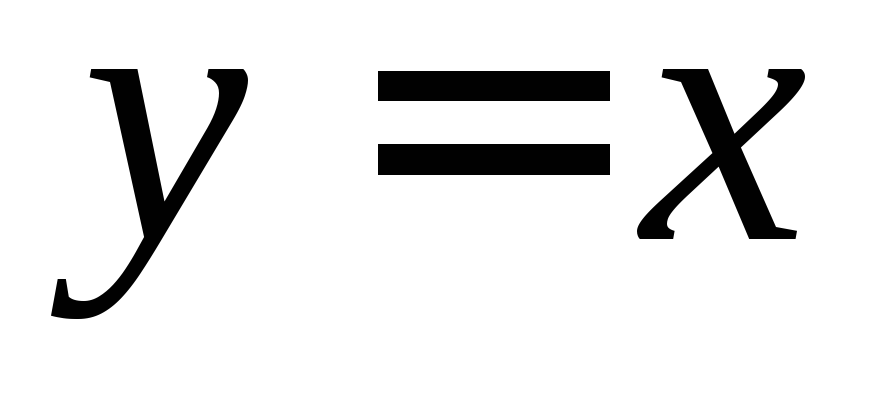 ,
, ,
, .
. ,
,
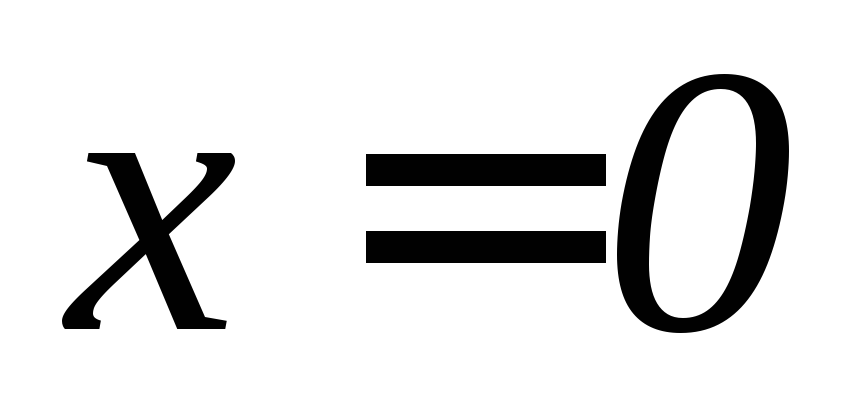 ,
, ,
, ,
, .
.
С помощью замены
переменных вычислить тройные интегралы
по областям
![]() ,
ограниченным указанными поверхностями:
,
ограниченным указанными поверхностями:
 ,
,
 ,
, .
. ,
,
 ,
, ,
, ,
,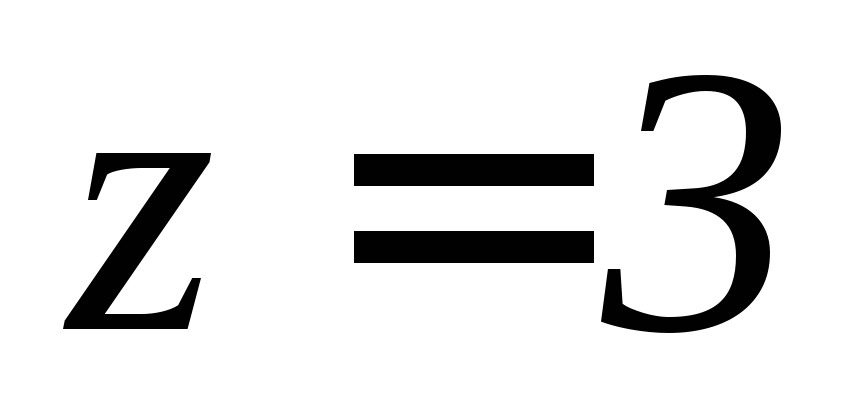 .
. ,
,
 ,
,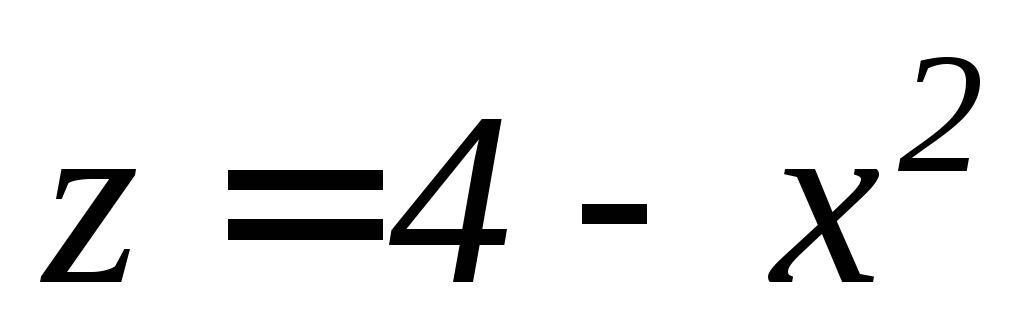 ,
, .
. ,
часть шара
,
часть шара
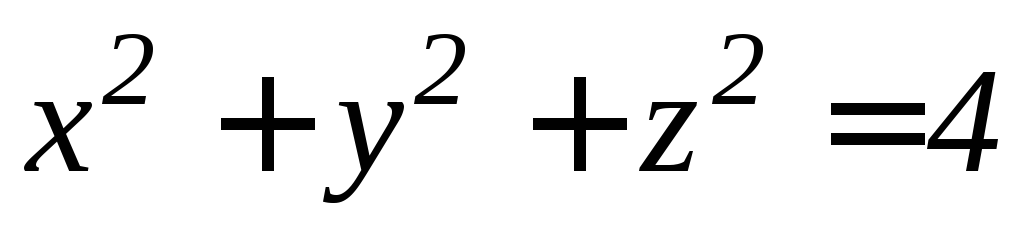 ,
находящаяся вI
октанте.
,
находящаяся вI
октанте. ,
,
 .
. ,
,
 ,
,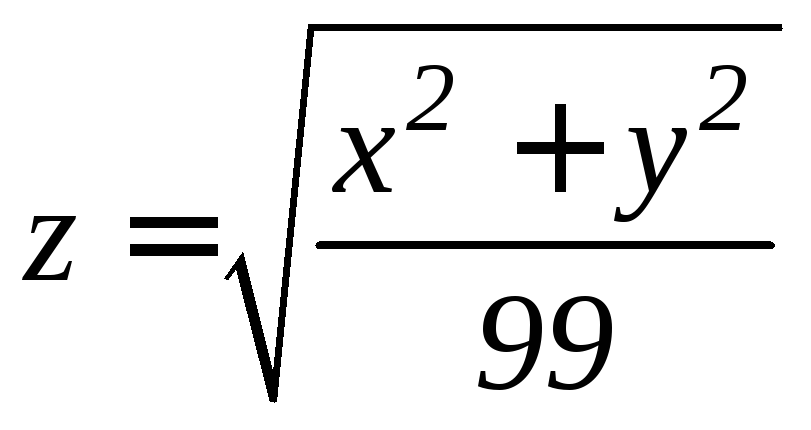 .
.
Вычислить объем тела, ограниченного заданными поверхностями:
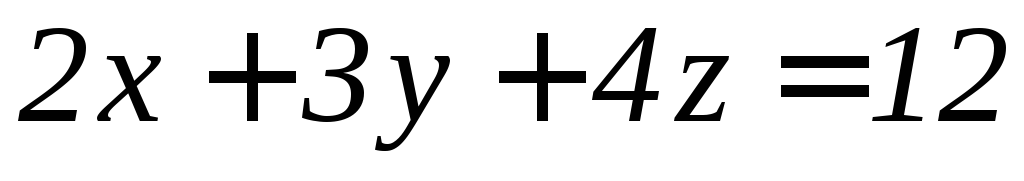 ,
,
 ,
,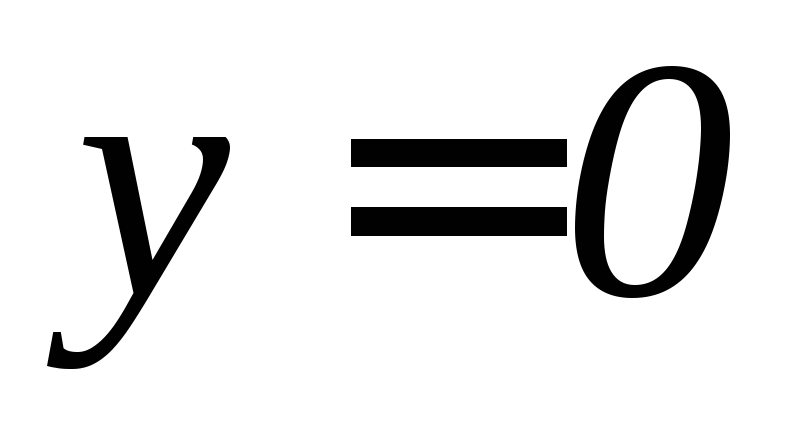 ,
, .
.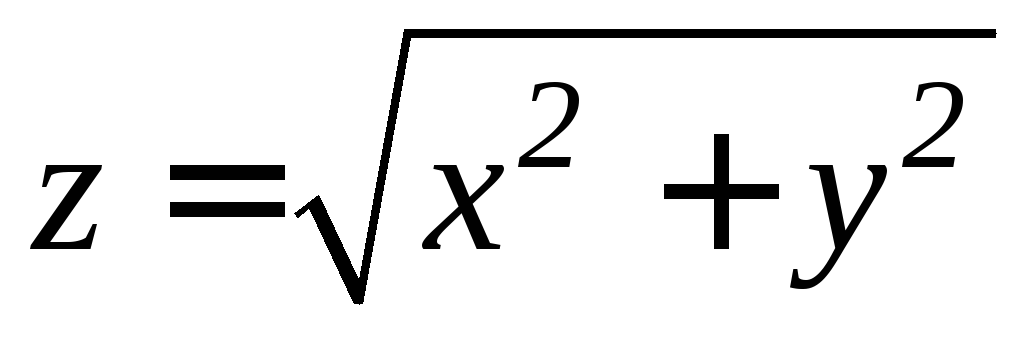 ,
,
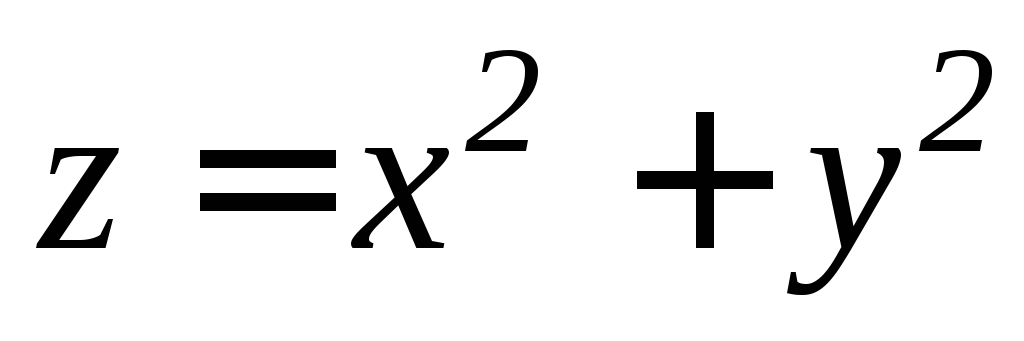 .
. ,
,
 ,
, .
.Найти массу куба
 ,
,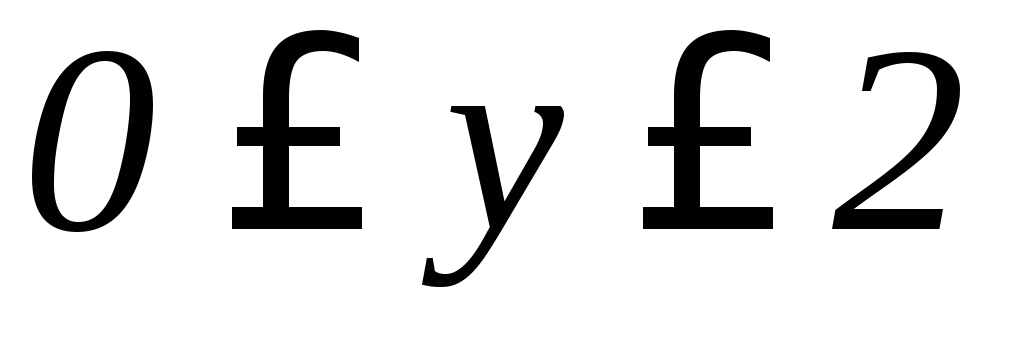 ,
, ,
если плотность в точке
,
если плотность в точке .
.
Найти координаты центра тяжести однородного тела, ограниченного заданными поверхностями:
 ,
,
 ,
, ,
, ,
, .
.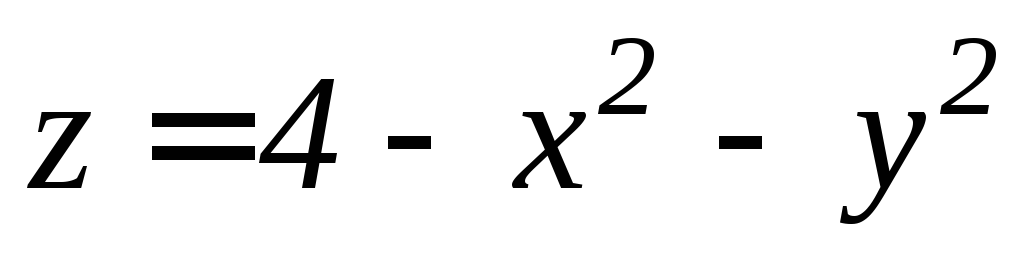 ,
,
 ,
, ,
, (
( ,
, ).
).Найти момент инерции относительно оси
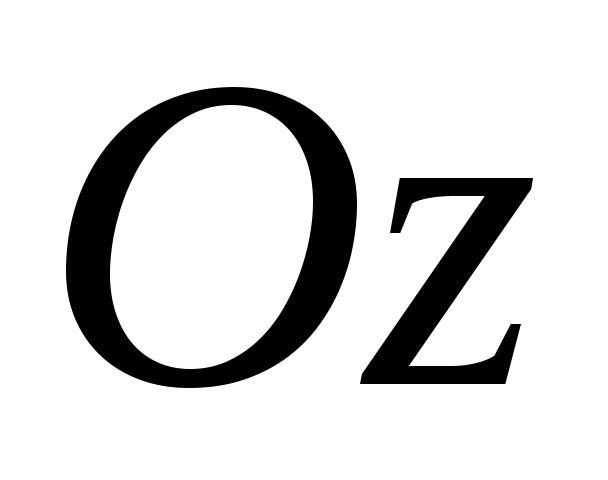 однородного тела, ограниченного
поверхностями
однородного тела, ограниченного
поверхностями ,
, ,
, ,
,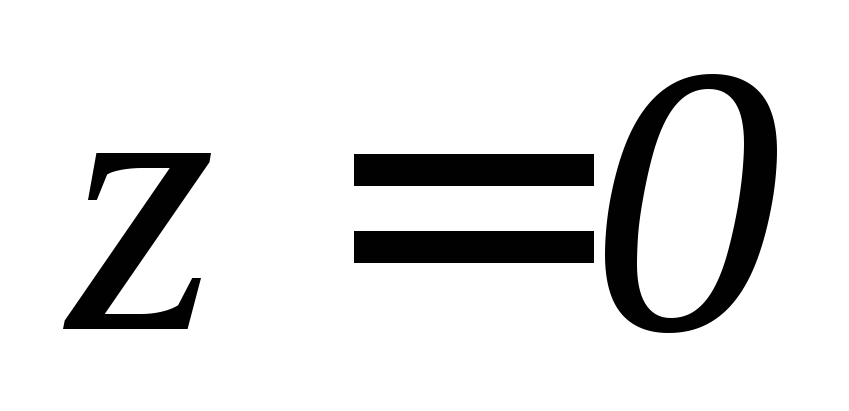 ,
, .
.Найти моменты инерции относительно координатных осей и начала координат однородной пирамиды, ограниченной плоскостями
 ,
,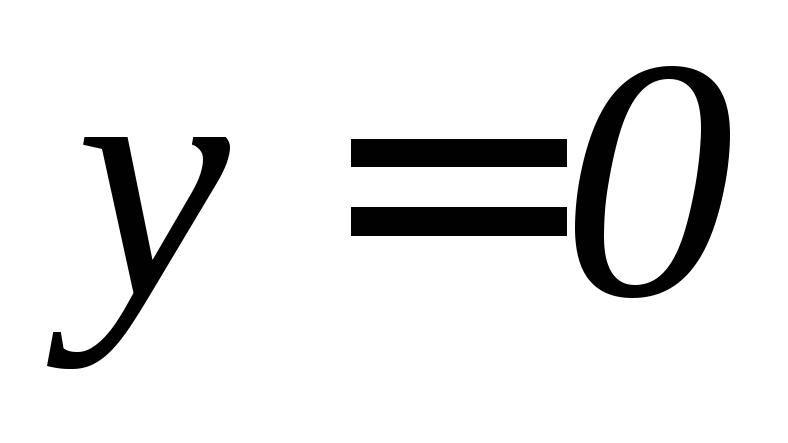 ,
, ,
, .
.
Задание 12.1. Начертить области интегрирования и изменить порядок интегрирования в следующих двойных интегралах:
|
1. |
а) |
|
|
б) |
|
|
2. |
а) |
|
|
б) |
|
|
3. |
а) |
|
|
б) |
|
|
4. |
а) |
|
|
б) |
|
|
5. |
а) |
|
|
б) |
|
|
6. |
а) |
|
|
б) |
|
|
7. |
а) |
|
|
б) |
|
|
8. |
а) |
|
|
б) |
|
|
9. |
а) |
|
|
б) |
|
|
10. |
а) |
|
|
б) |
|
|
11. |
а) |
|
|
б) |
|
|
12. |
а) |
|
|
б) |
|
|
13. |
а) |
|
|
б) |
|
|
14. |
а) |
|
|
б) |
|
|
15. |
а) |
|
|
б) |
|
|
16. |
а) |
|
|
б) |
|
|
17. |
а) |
|
|
б) |
|
|
18. |
а) |
|
|
б) |
|
|
19. |
а) |
|
|
б) |
|
|
20. |
а) |
|
|
б) |
|
|
21. |
а) |
|
|
б) |
|
|
22. |
а) |
|
|
б) |
|
|
23. |
а) |
|
|
б) |
|
|
24. |
а) |
|
|
б) |
|
|
25. |
а) |
|
|
б) |
|
Задание 12.2.
Вычислить двойные интегралы по областям![]() ,
ограниченным указанными линиями. Область
,
ограниченным указанными линиями. Область![]() изобразить на чертеже:
изобразить на чертеже:
а)
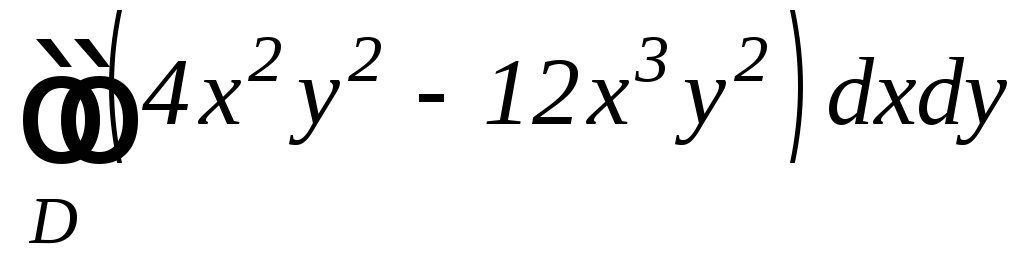 ,
, ,
, ,
, .
.
б)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
а)
 ,
, ,
, ,
, ,
, .
.
б)
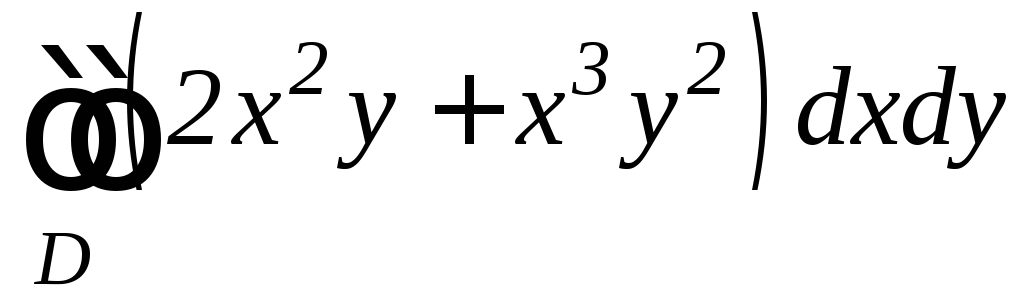 ,
,![]() ,
,![]() ,
,![]() .
.
а)
 ,
, ,
, ,
, ,
, .
.
б)
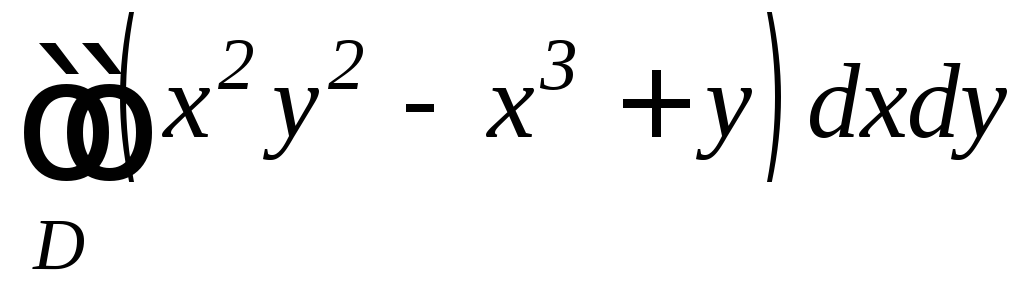 ,
,
![]() ,
,
![]() ,
,![]() .
.
а)
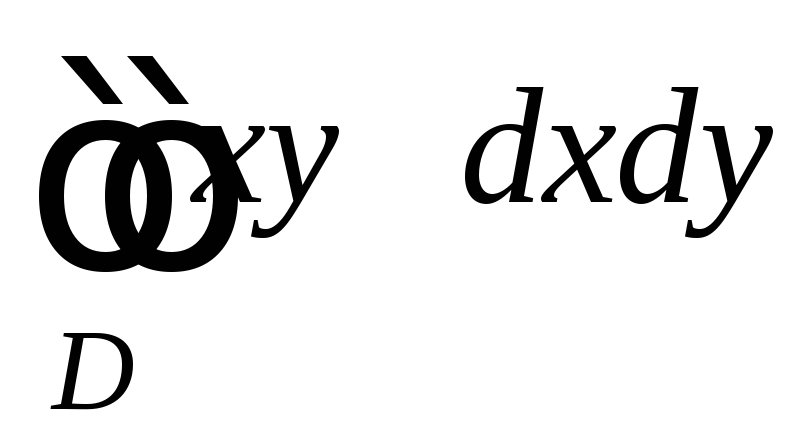 ,
, ,
, ,
, ,
, .
.
б)
 ,
,
![]() ,
,
![]() ,
,![]() .
.
а)
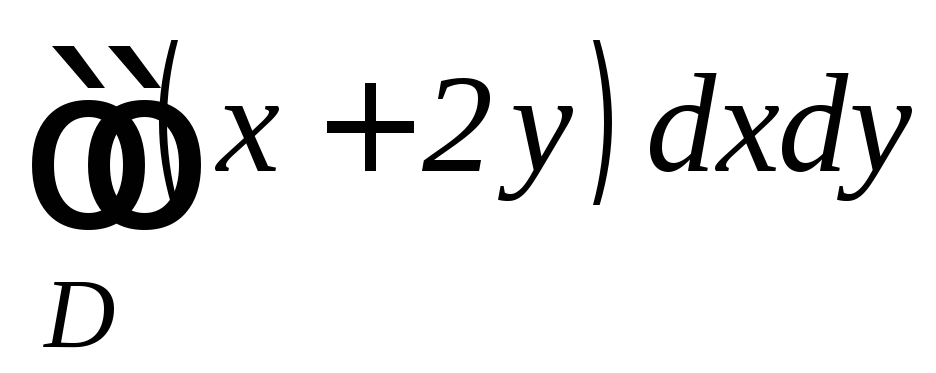 ,
, ,
, ,
,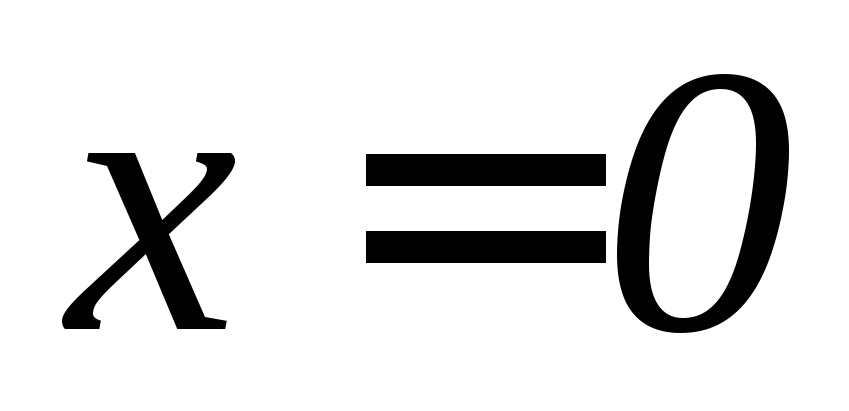 ,
, .
.
б)
 ,
,
![]() ,
,![]() ,
,
![]() .
.
а)
 ,
, ,
, ,
, ,
, .
.
б)
 ,
,
![]() ,
,![]() ,
,![]() .
.
а)
 ,
, ,
, ,
, ,
, .
.
б)
 ,
,
![]() ,
,![]() (
(![]() ).
).
а)
 ,
,
 ,
,
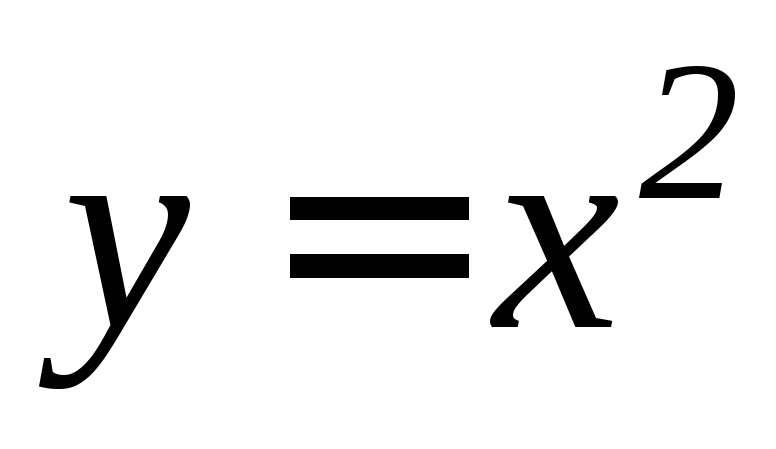 .
.
б)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
а)
 ,
, ,
, ,
,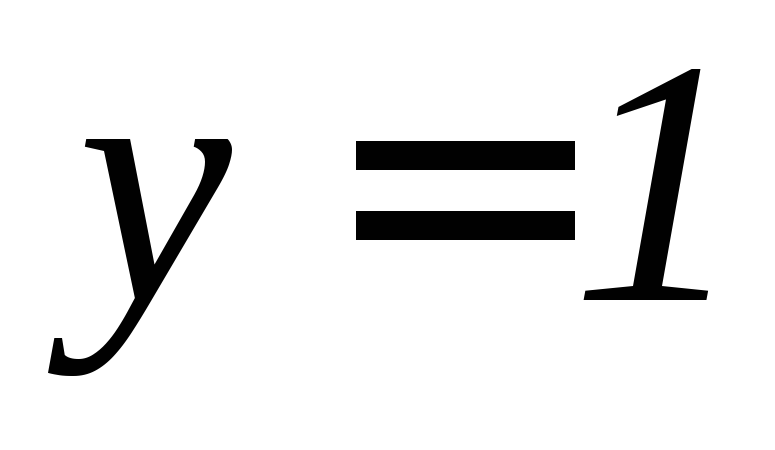 ,
, .
.
б)
![]() ,
,
![]() ,
,![]() (
(![]() ).
).
а)
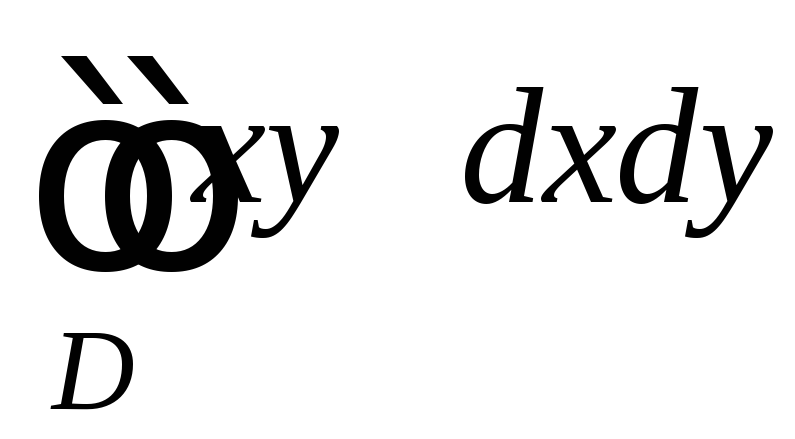 ,
, ,
, .
.
б)
 ,
,
![]() ,
,![]() ,
,![]() .
.
а)
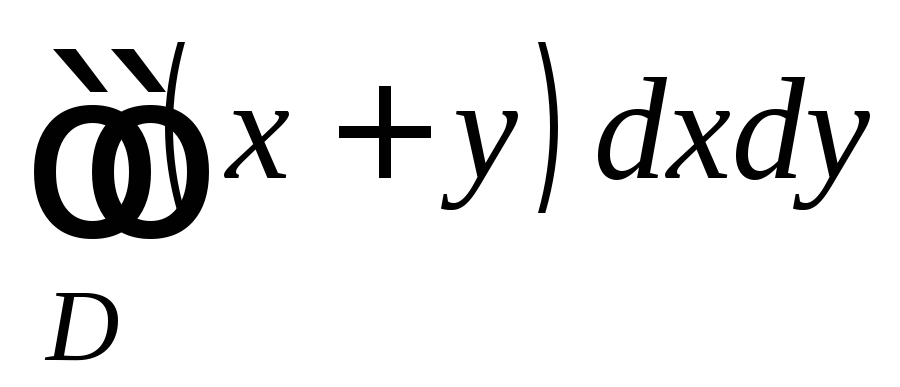 ,
, ,
, ,
, .
.
б)
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
а)
 ,
,
 ,
,
 ,
,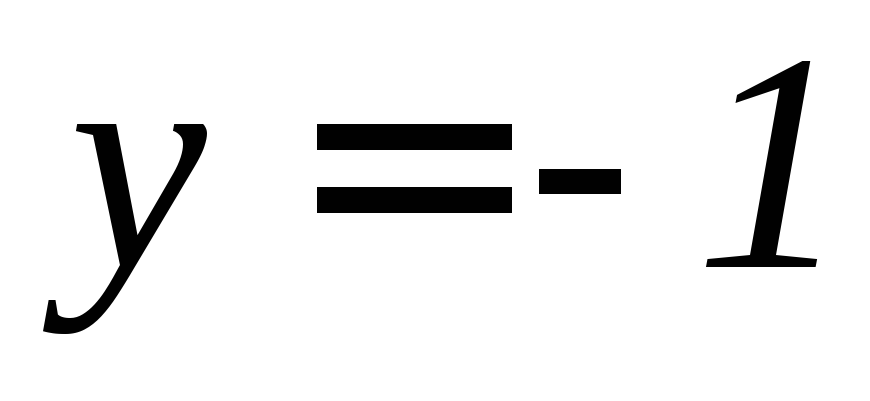 .
.
б)
![]() ,
,![]() ,
,![]() ,
,![]() .
.
а)
 ,
, ,
, ,
,
 .
.
б)
 ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
а)
 ,
, ,
, ,
,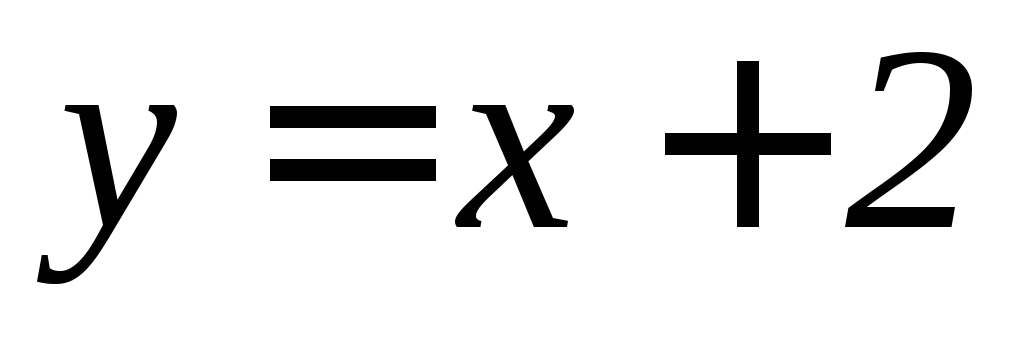 ,
, .
.
б)
![]() ,
,
![]() ,
,![]() .
.
а)
 ,
,
 ,
, .
.
б)
![]() ,
,![]() ,
,![]() ,
,![]() .
.
а)
 ,
, ,
,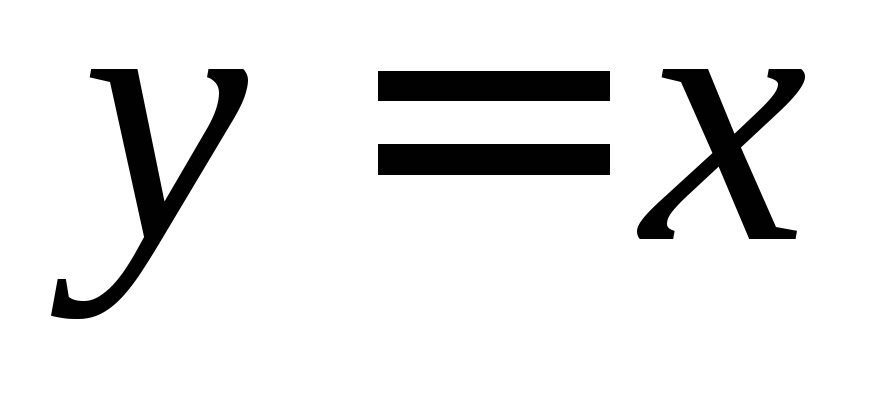 ,
, .
.
б)
![]() ,
,
![]() ,
,![]() .
.
а)
 ,
,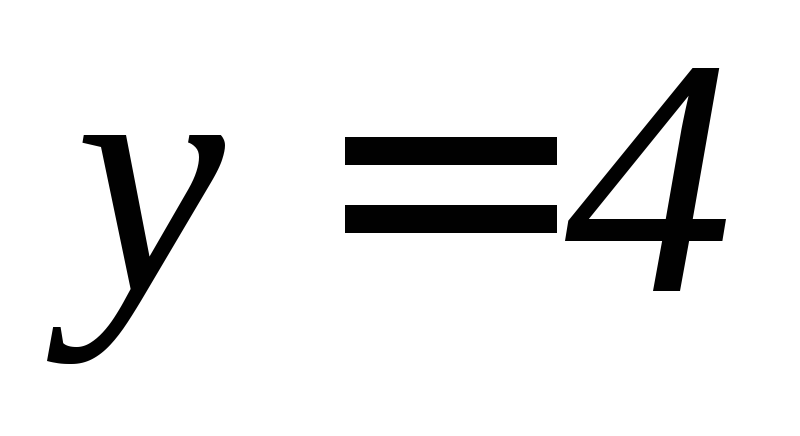 ,
, ,
,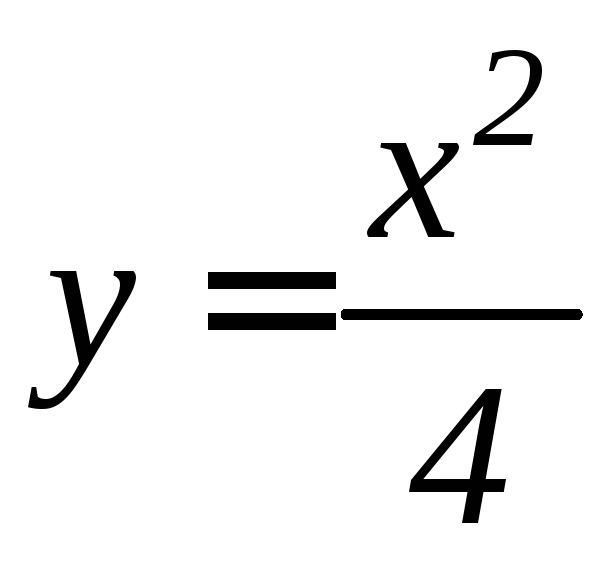 (
( ).
).
б)
![]() ,
,
![]() ,
,
![]() .
.
а)
 ,
, ,
, ,
, .
.
б)
![]() ,
,
![]() ,
,![]() .
.
а)
 ,
,
 ,
, ,
, .
.
б)
![]() ,
,![]() ,
,![]() ,
,![]() .
.
а)
 ,
,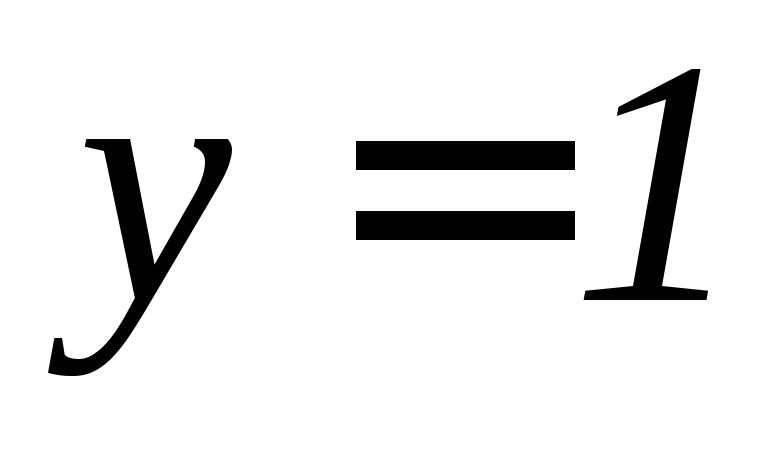 ,
, ,
, .
.
б)
![]() ,
,![]() ,
,![]() ,
,![]() .
.
а)
 ,
,
 ,
, .
.
б)
 ,
,![]() ,
,![]() ,
,![]() .
.
а)
 ,
, ,
,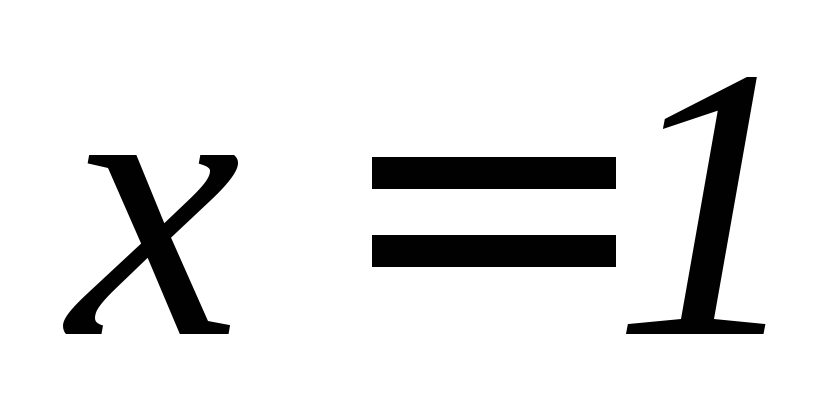 ,
, ,
, .
.
б)
![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
а)
 ,
, ,
, ,
,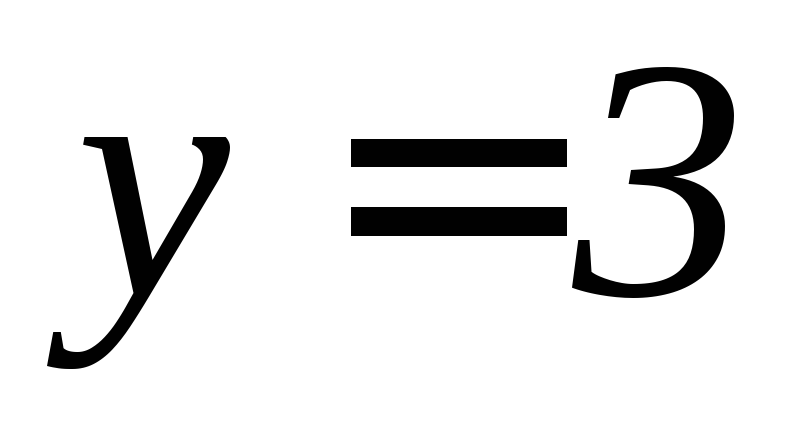 ,
, .
.
б)
![]() ,
,
![]() ,
,![]() .
.
а)
 ,
, ,
, ,
, ,
, .
.
б)
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
а)
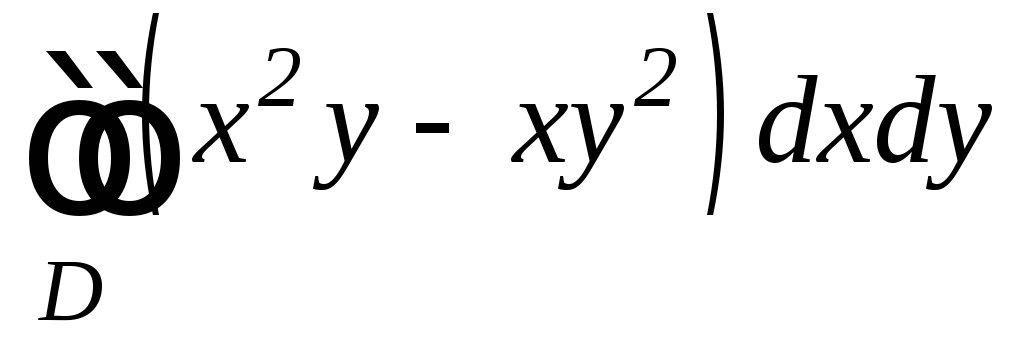 ,
, ,
,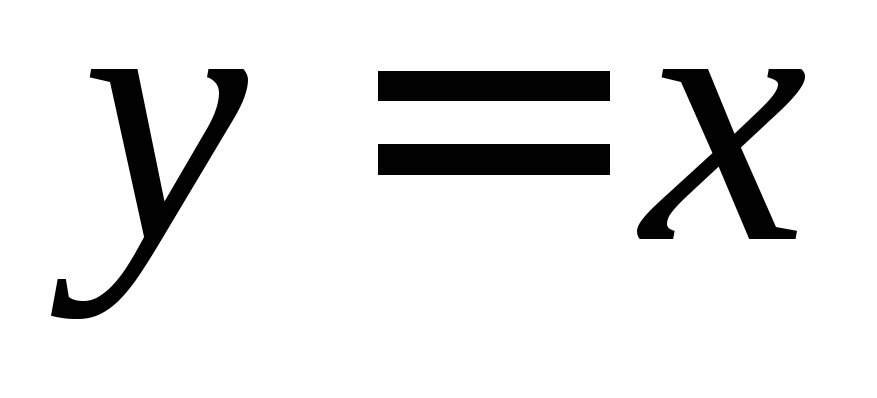 ,
, .
.
б)
![]() ,
,
![]() ,
,![]() .
.
Задание 12.3.
Вычислить двойные интегралы по областям![]() ,
ограниченным указанными линиями, с
помощью перехода к полярным координатам.
Сделать чертеж области
,
ограниченным указанными линиями, с
помощью перехода к полярным координатам.
Сделать чертеж области![]() :
:
а)
 ,
,
 ,
,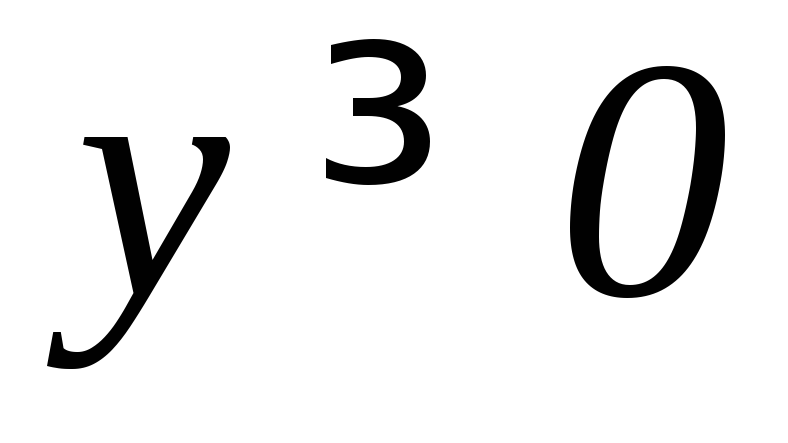 .
.
б)
 ,
,
![]() ,
,![]() ,
,![]() .
.
а)
 ,
, ,
, ,
,
 .
.
б)
![]() ,
,
![]() ,
,![]() .
.
а)
 ,
, ,
, .
.
б)
 ,
,
![]() ,
,![]() .
.
а)
 ,
, ,
,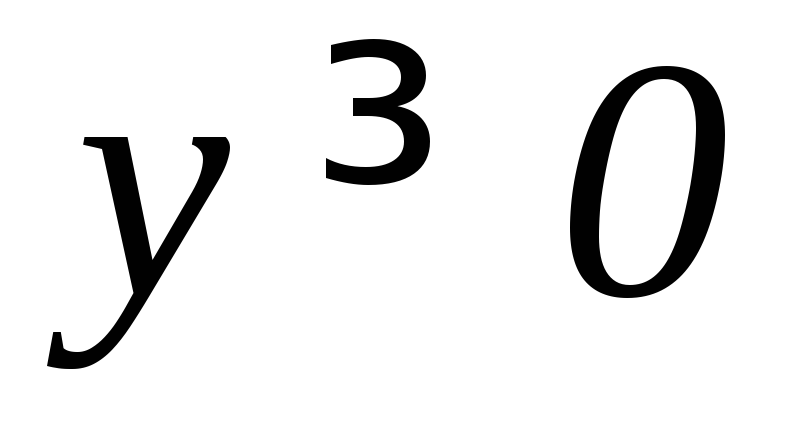 .
.
б)
 ,
,
![]() ,
,![]() .
.
а)
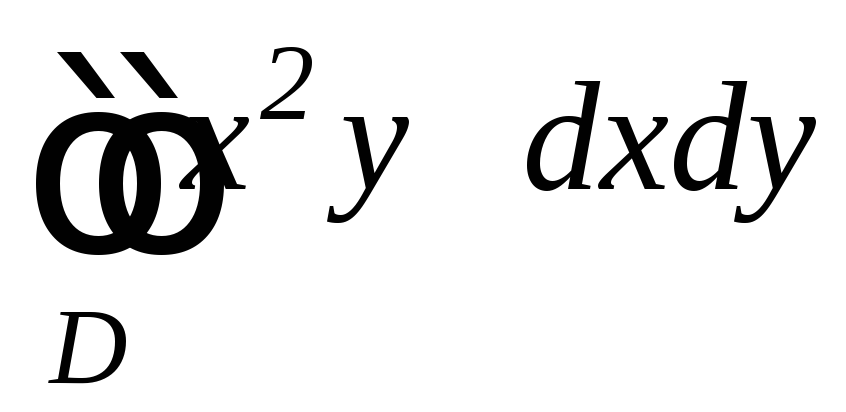 ,
,
 ,
,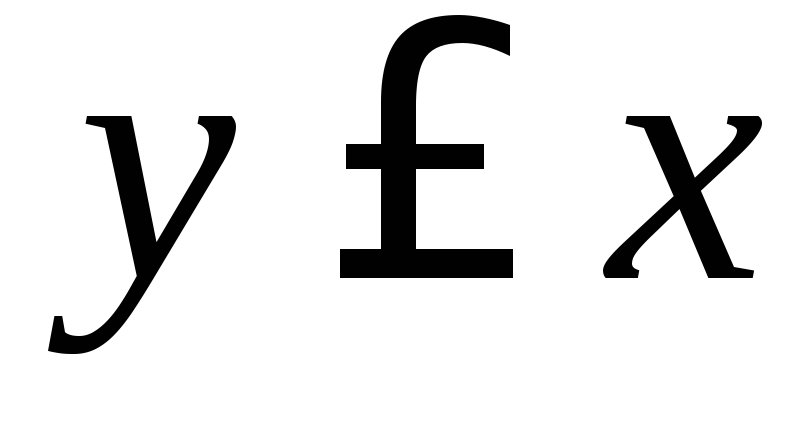 .
.
б)
 ,
,
![]() .
.
а)
 ,
,
 ,
,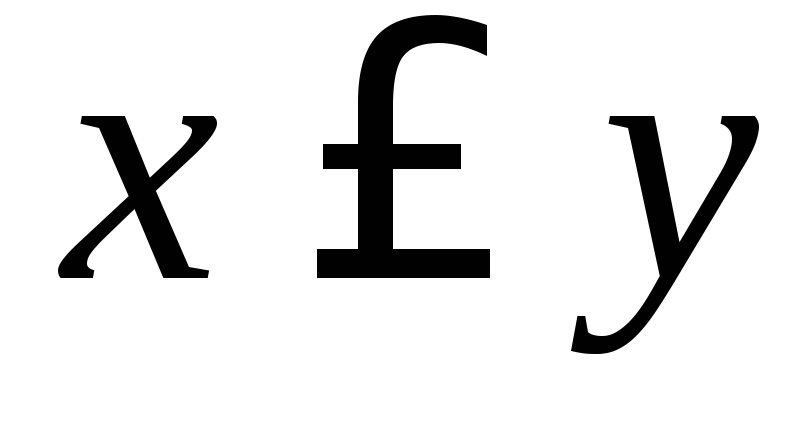 .
.
б)
 ,
,
![]() ,
, ,
,![]() .
.
а)
 ,
, .
.
б)
 ,
,
![]() ,
,![]() .
.
а)
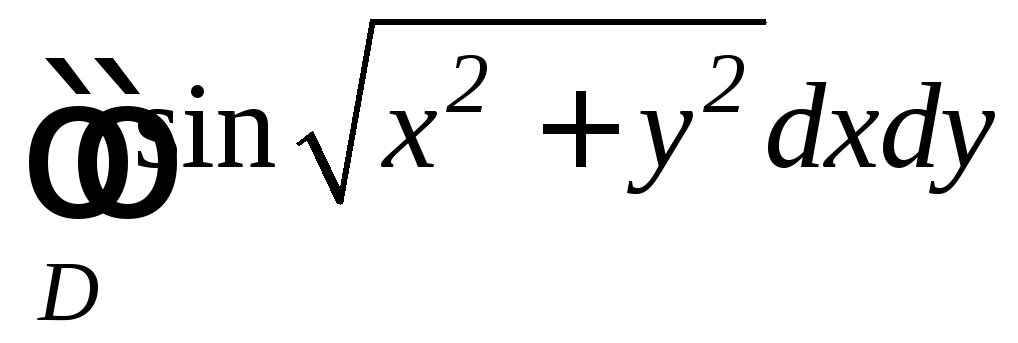 ,
, ,
, .
.
б)
 ,
,
![]() ,
,![]() .
.
а)
 ,
,
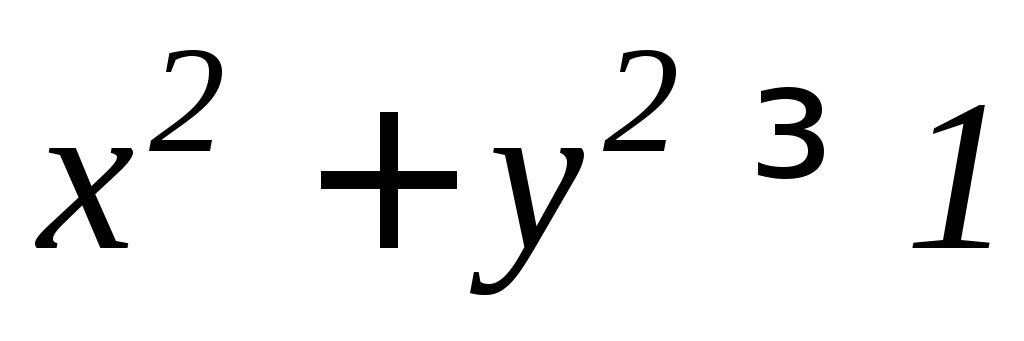 ,
, .
.
б)
 ,
,
![]() ,
,![]() .
.
а)
 ,
, ,
, ,
,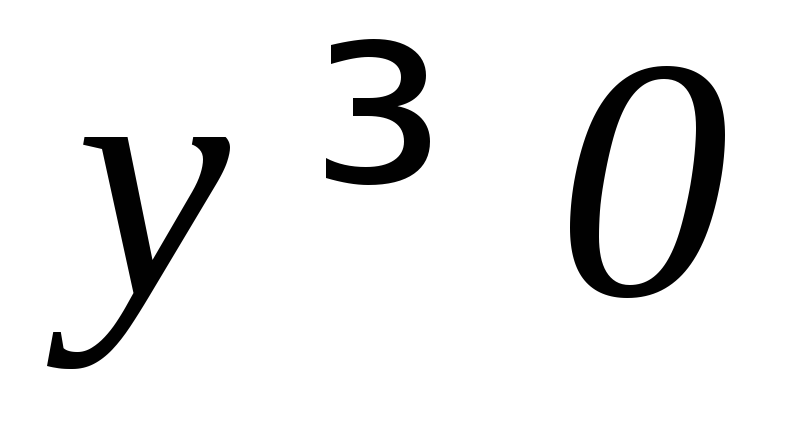 .
.
б)
 ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
а)
 ,
,
 ,
, ,
, .
.
б)
 ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
а)
 ,
,
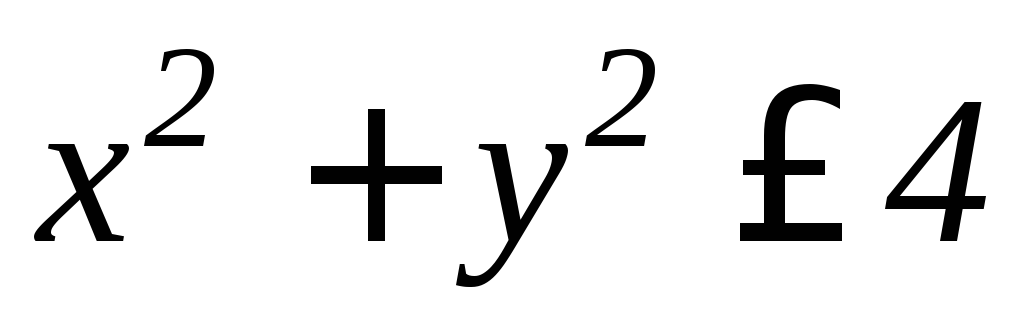 ,
, .
.
б)
![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
а)
 ,
,
 ,
, ,
, .
.
б)
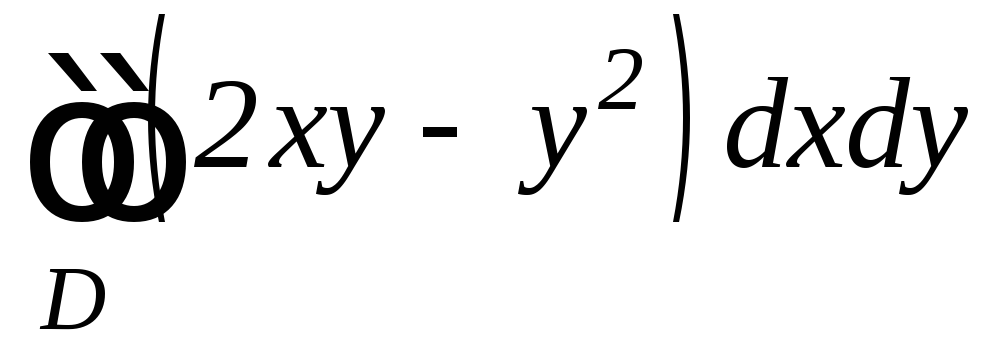 ,
,
![]() ,
,![]() ,
,
![]() .
.
а)
 ,
,
 ,
, ,
,
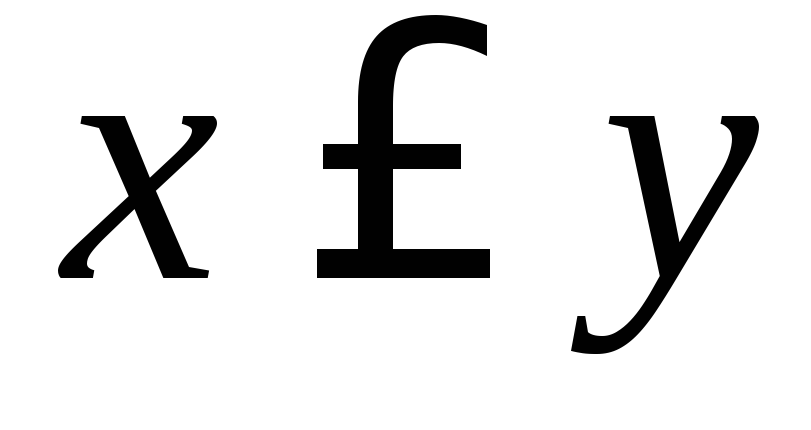 .
.
б)
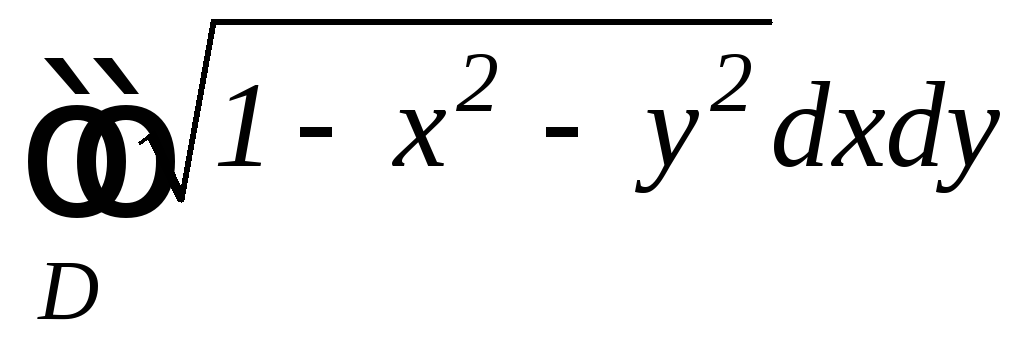 ,
,
![]() .
.
а)
 ,
, .
.
б)
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
а)
 ,
,
 ,
, .
.
б)
 ,
,
![]() ,
,![]() .
.
а)
 ,
,
 ,
, .
.
б)
 ,
,
![]() .
.
а)
 ,
,
 ,
, ,
,
 ,
, .
.
б)
![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
а)
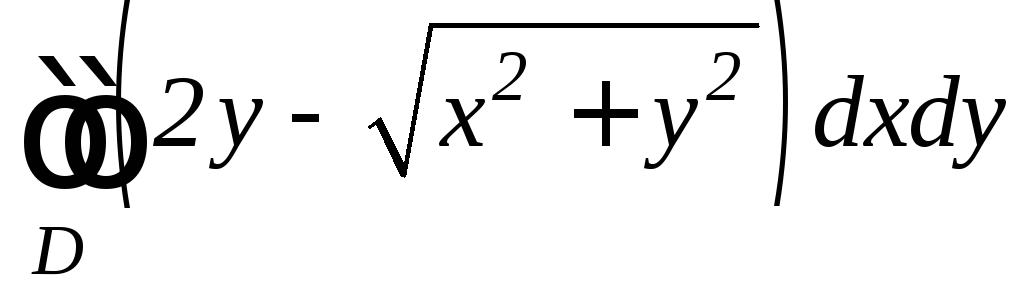 ,
,
 ,
,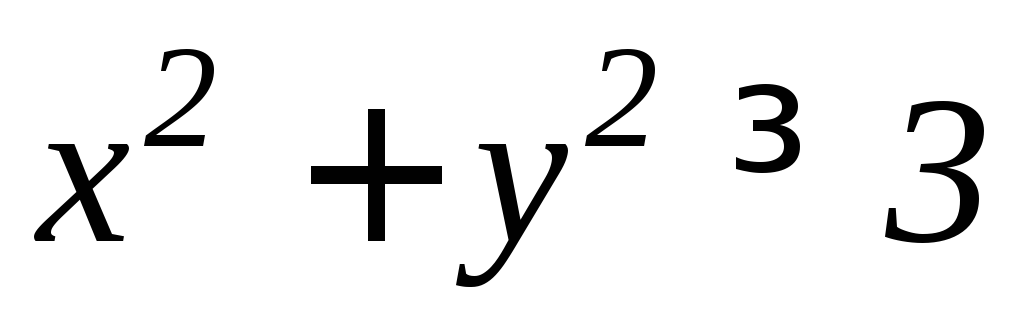 .
.
б)
 ,
,
![]() .
.
а)
 ,
,
 .
.
б)
 ,
,
![]() .
.
а)
 ,
,
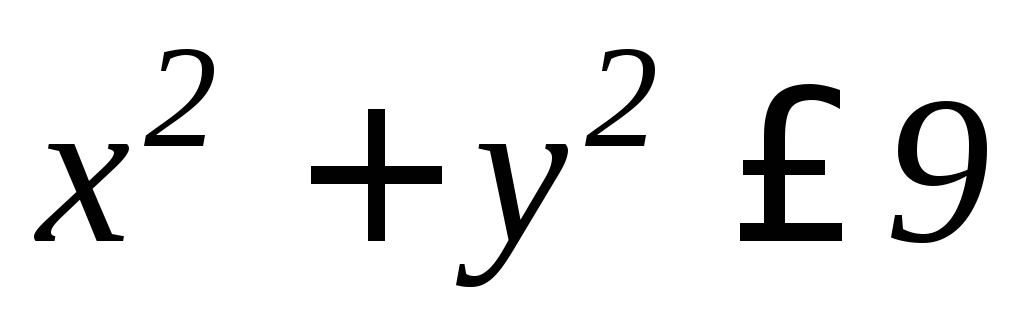 ,
, ,
,
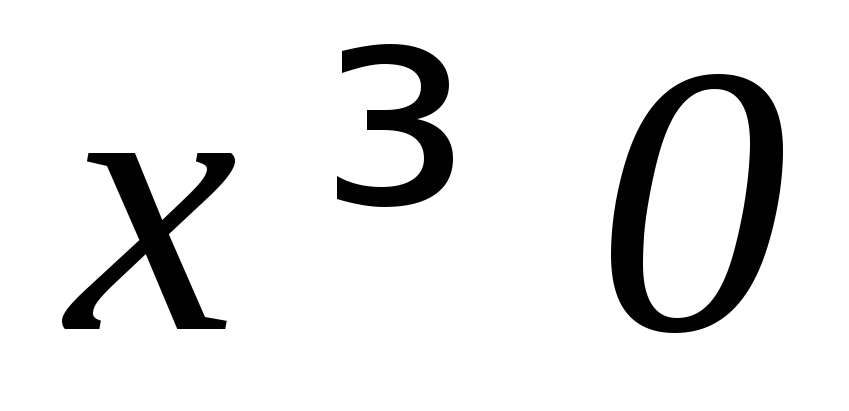 ,
, .
.
б)
 ,
,
![]() .
.
а)
 ,
,
 .
.
б)
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
а)
 ,
,
 ,
, .
.
б)
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
а)
 ,
,
 ,
, .
.
б)
 ,
,
![]() ,
,![]() .
.
а)
 ,
,
 ,
, .
.
б)
 ,
,
![]() .
.
Задание 12.4.
С помощью двойного интеграла вычислить
площадь области
![]() ,
ограниченной указанными линиями; сделать
чертеж:
,
ограниченной указанными линиями; сделать
чертеж:
|
1. |
|
|
2. |
| ||
|
3. |
|
|
4. |
| ||
|
5. |
|
|
6. |
| ||
|
7. |
|
|
8. |
| ||
|
9. |
|
| ||||
|
10. |
|
|
11. |
| ||
|
12. |
|
|
13. |
| ||
|
14. |
|
|
15. |
| ||
|
16. |
|
|
17. |
| ||
|
18. |
|
|
19. |
| ||
|
20. |
|
|
21. |
| ||
|
22. |
|
|
23. |
| ||
|
24. |
|
|
25. |
| ||
Задание 12.5. С помощью двойного интеграла вычислить объем тела, ограниченного заданными поверхностями:
 ,
,
 ,
,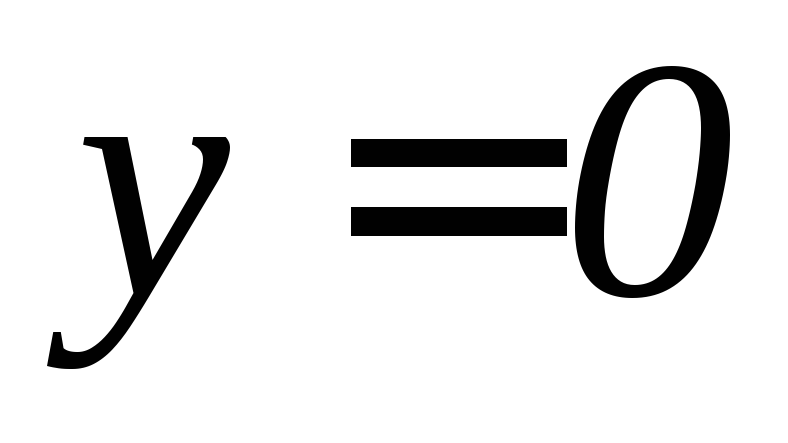 ,
, .
. ,
,
 ,
, ,
, .
. ,
,
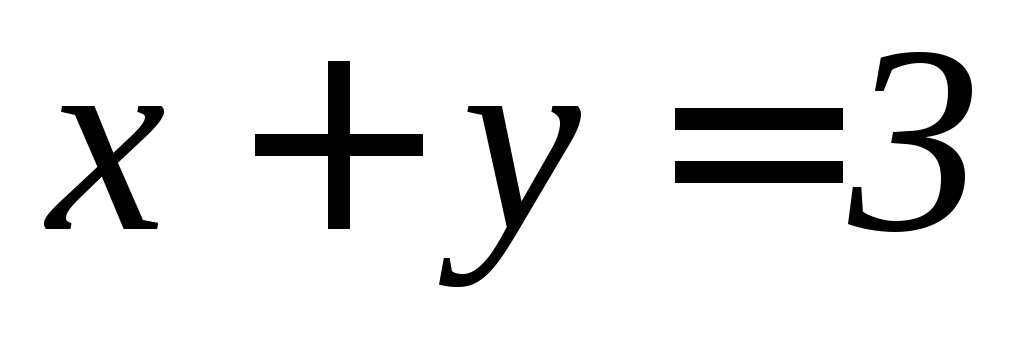 ,
, ,
, ,
, .
.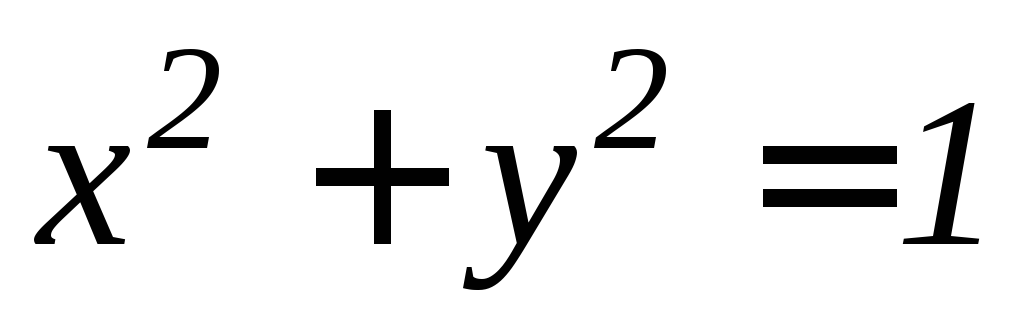 ,
,
 ,
, .
. ,
,
 .
. ,
,
 ,
, ,
, .
. ,
,
 .
. ,
,
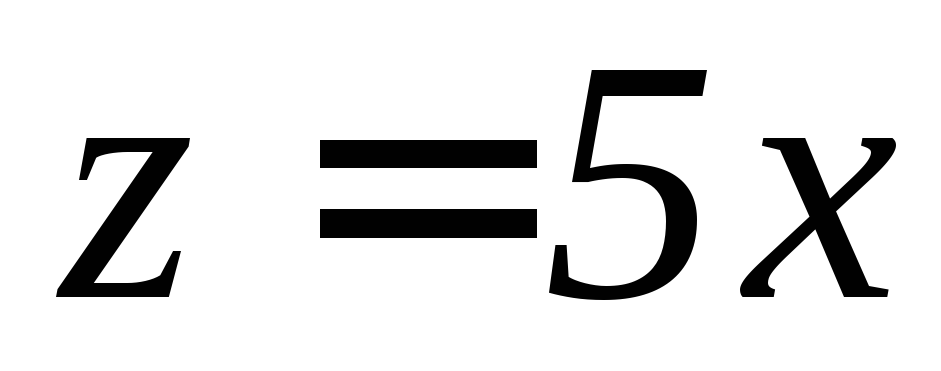 ,
, .
. ,
,
 ,
,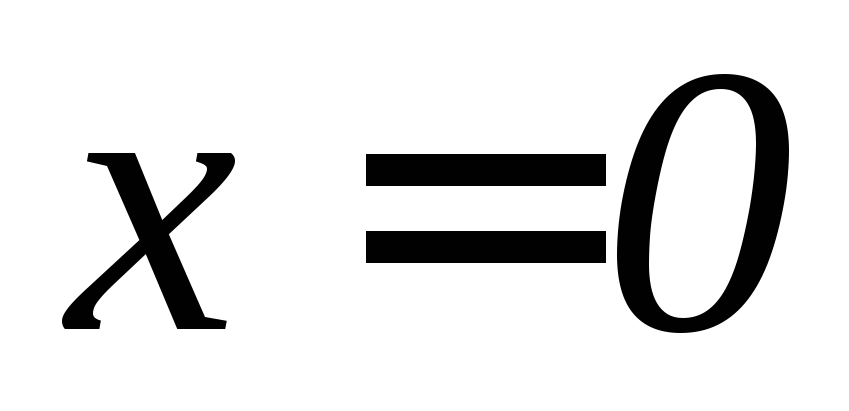 ,
, ,
, .
. ,
,
 ,
, ,
, ,
, .
.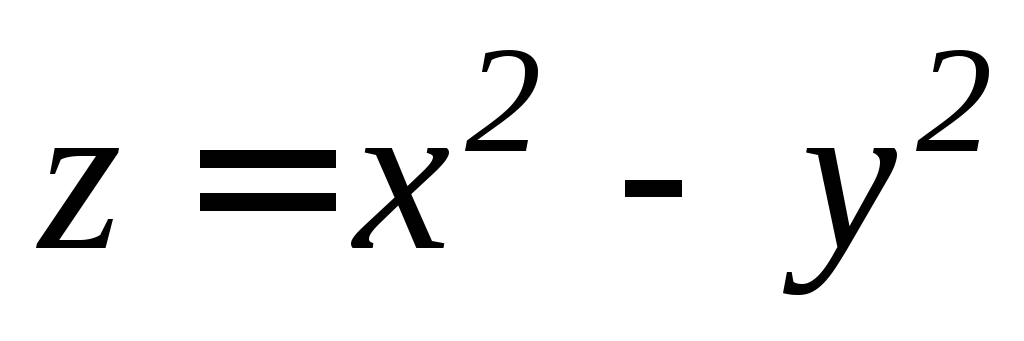 ,
,
 ,
, ,
, .
. ,
,
 ,
, .
. ,
,
 ,
, .
. ,
,
 .
. ,
,
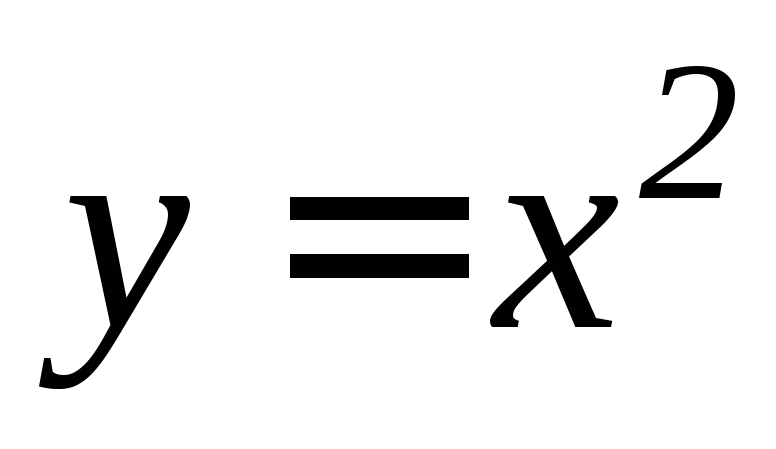 ,
, ,
, .
.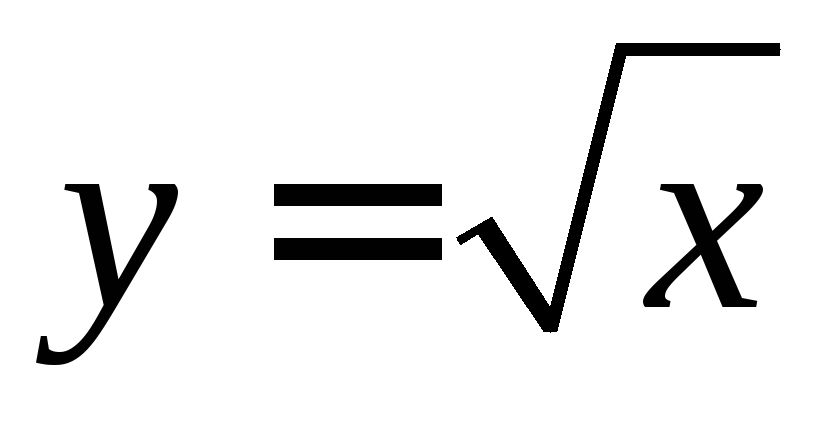 ,
,
 ,
,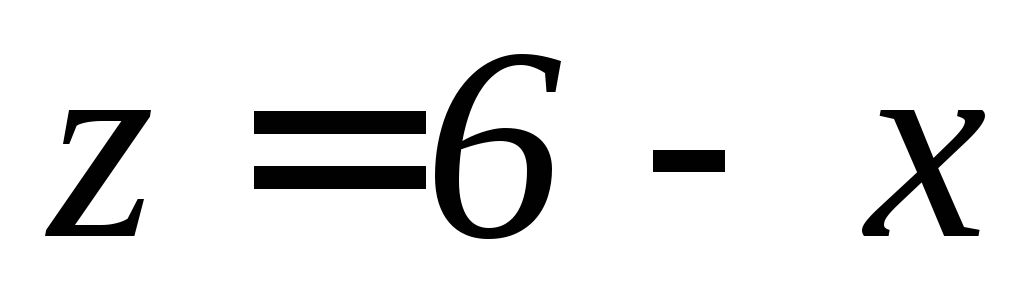 ,
, .
. ,
,
 ,
,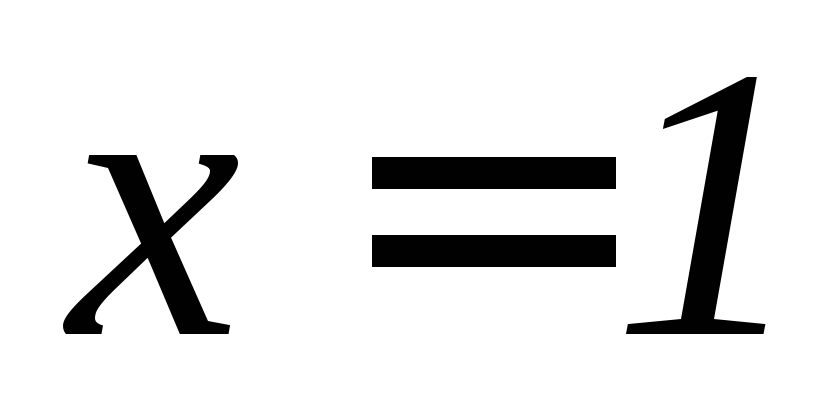 ,
, ,
,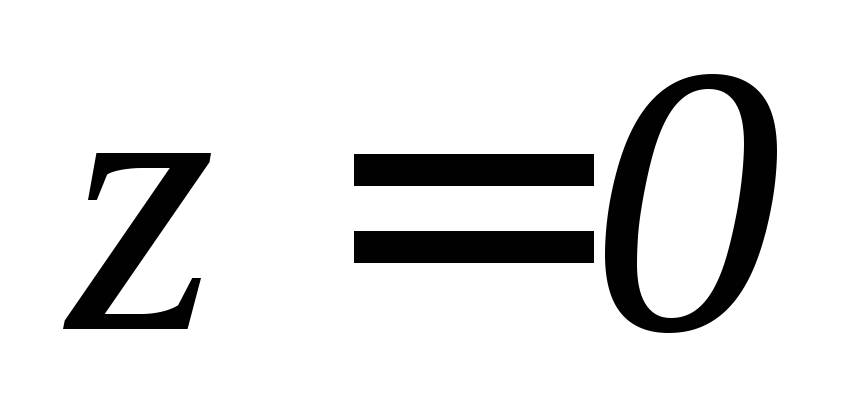 .
.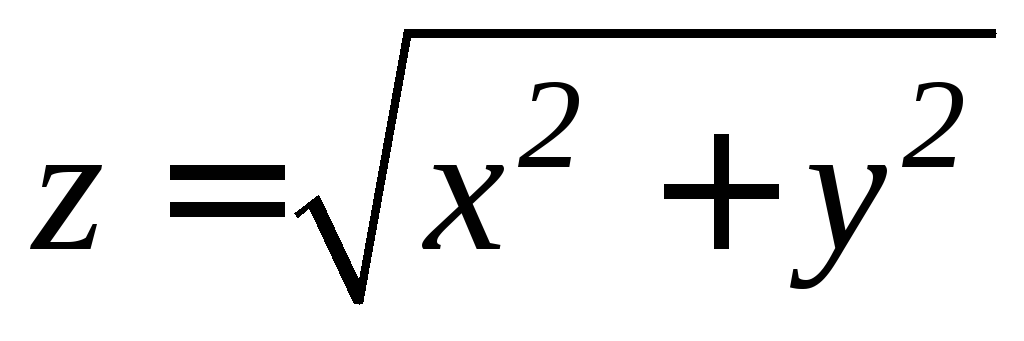 ,
,
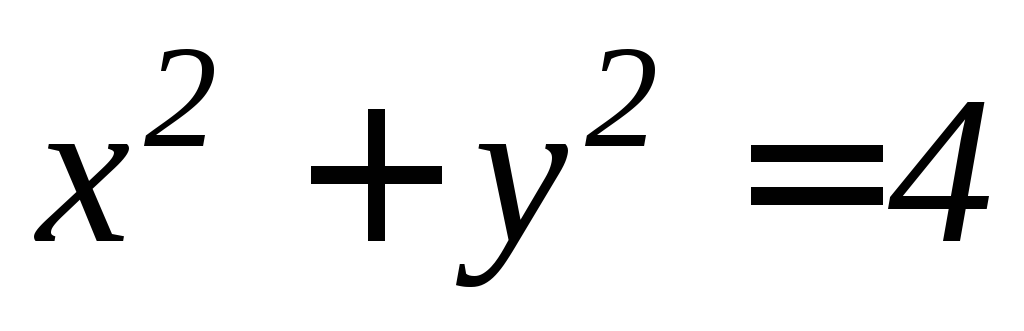 ,
, .
. ,
,
 ,
,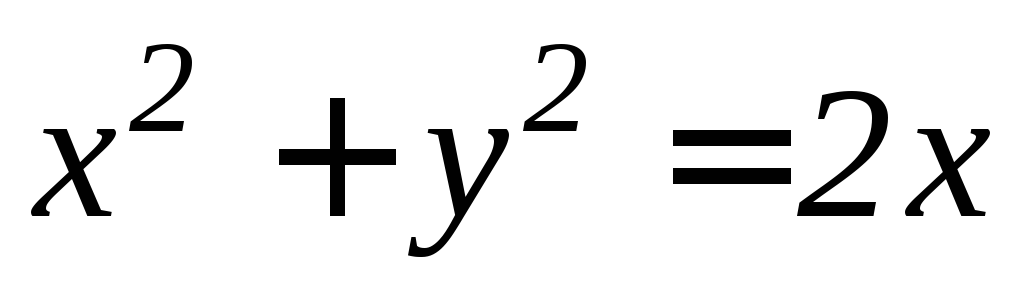 ,
, .
. ,
,
 ,
, ,
,
 ,
,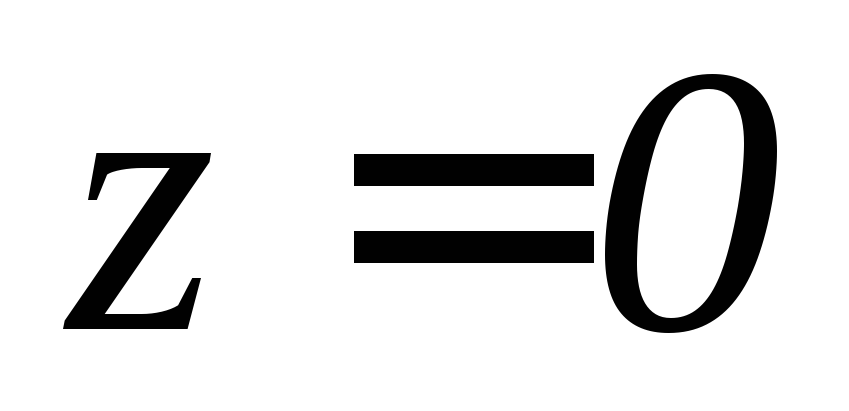 .
. ,
,
 ,
, .
. ,
,
 ,
, (
( ,
,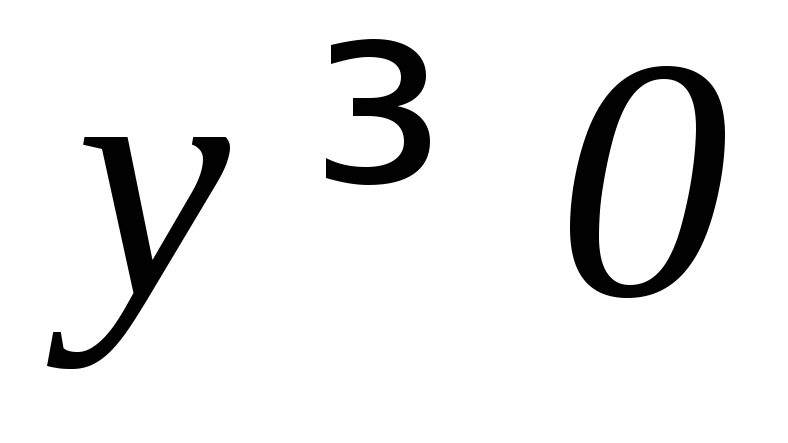 ,
, ).
). ,
,
 ,
, ,
,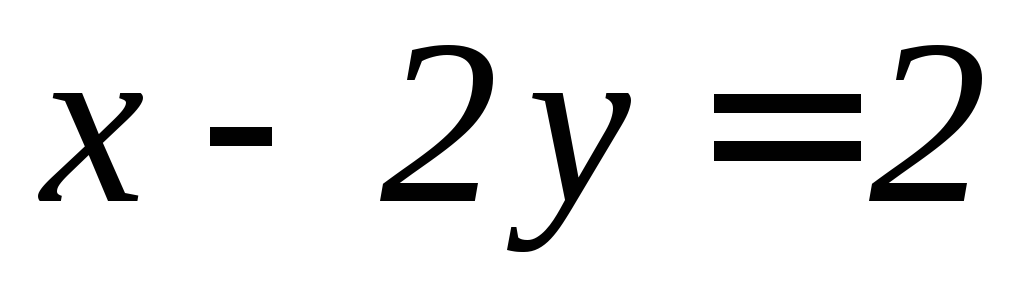 (
( ).
).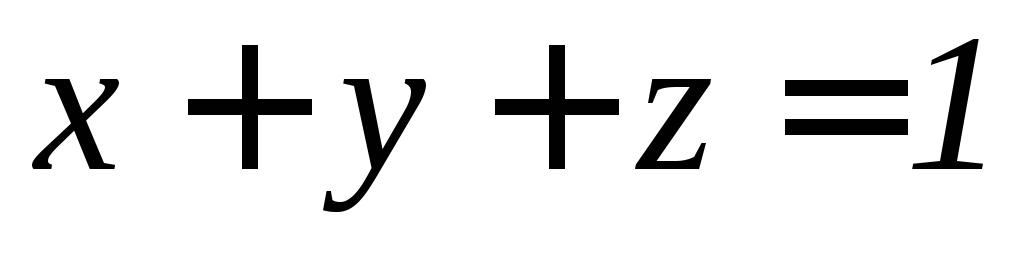 ,
,
 ,
,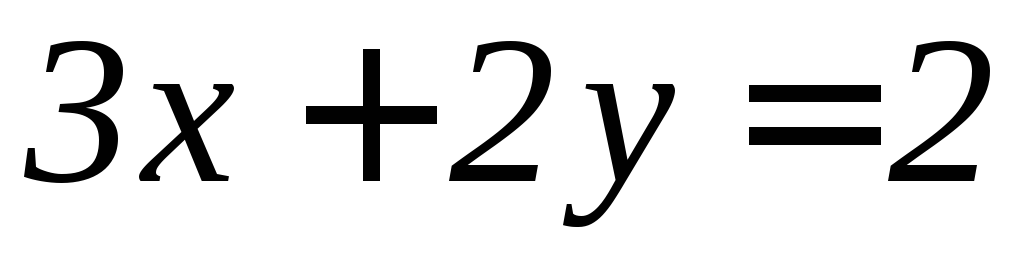 (
( ,
, ).
).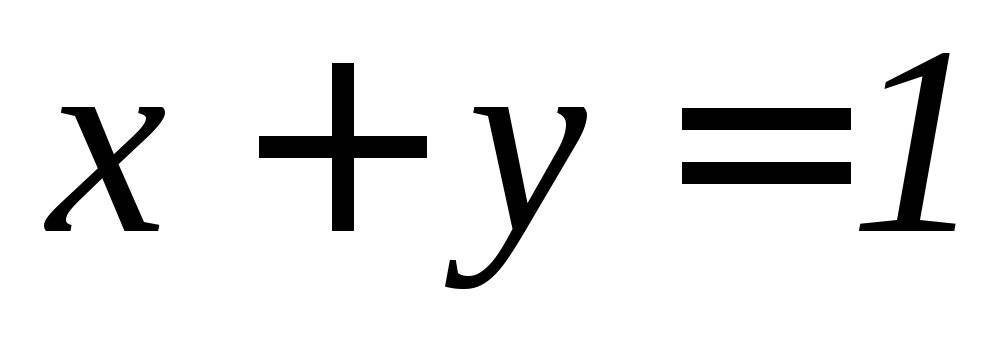 ,
,
 (
( ,
, ,
, ).
).
Задание 12.6. Вычислить площадь:
Части параболоида
 ,
вырезанной цилиндром
,
вырезанной цилиндром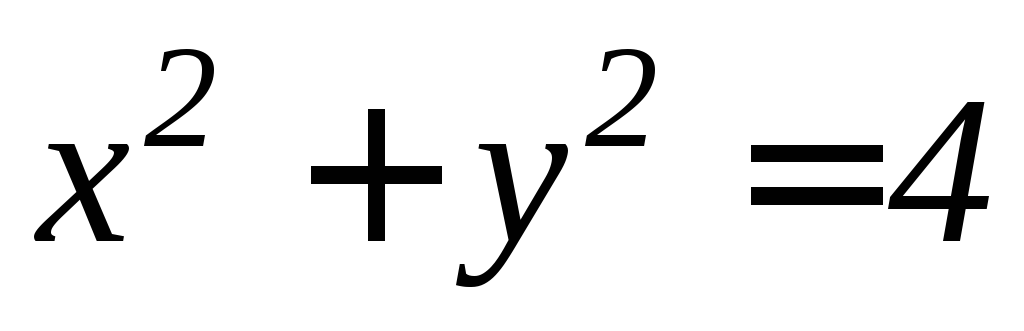 .
.Части плоскости
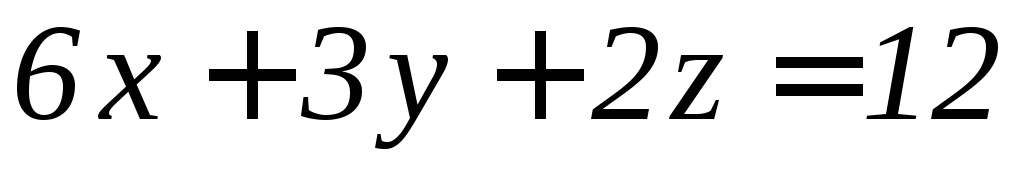 ,
лежащей вI
октанте.
,
лежащей вI
октанте.Части плоскости
 ,
отсекаемой плоскостями
,
отсекаемой плоскостями ,
, ,
, ,
, .
.Поверхности цилиндра
 ,
отсеченной плоскостями
,
отсеченной плоскостями ,
, ,
, .
.Части плоскости
 ,
вырезанной цилиндром
,
вырезанной цилиндром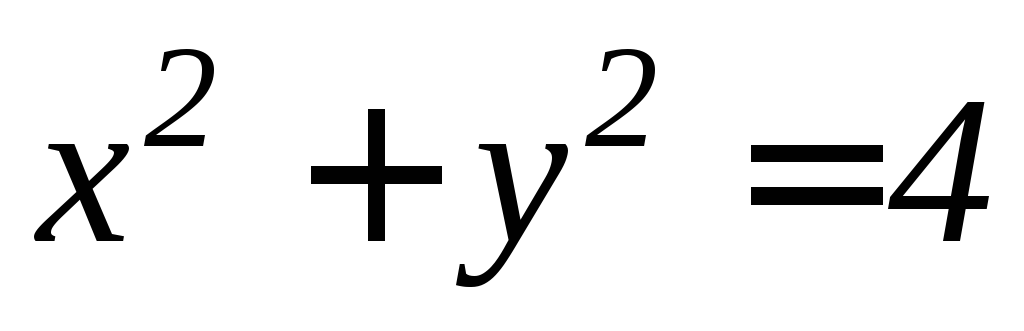 .
.Части параболоида
 ,
вырезанной цилиндром
,
вырезанной цилиндром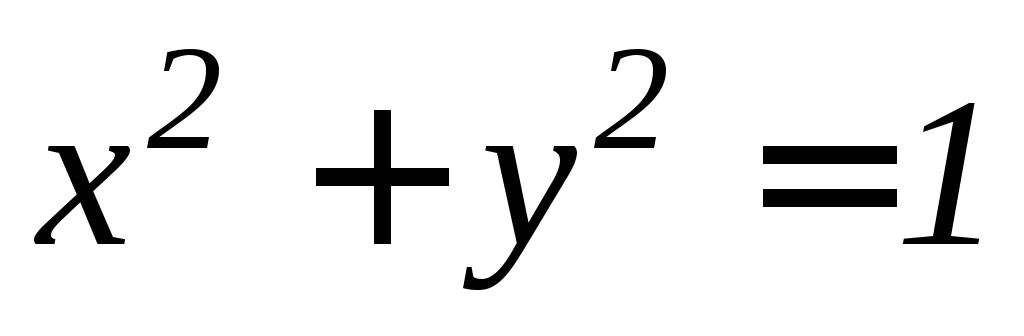 .
.Поверхности цилиндра
 ,
вырезанной цилиндром
,
вырезанной цилиндром и плоскостью
и плоскостью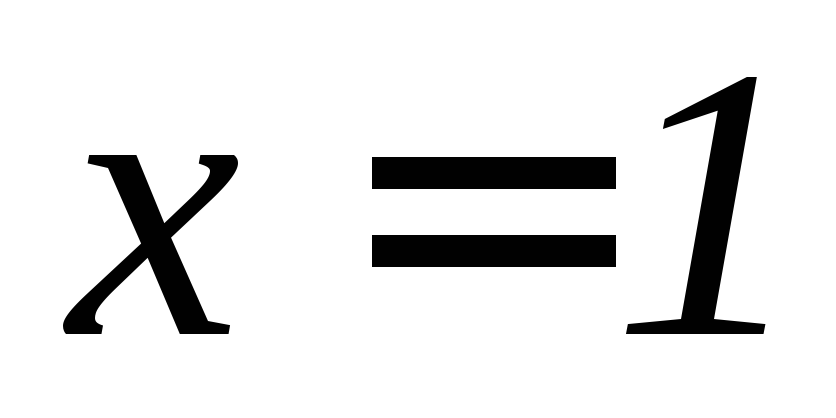 .
.Части цилиндра
 ,
вырезанной цилиндром
,
вырезанной цилиндром (
( ).
).Части параболоида
 ,
вырезанной цилиндром
,
вырезанной цилиндром .
.Части конуса
 ,
заключенной внутри цилиндра
,
заключенной внутри цилиндра .
.Части сферы
 ,
заключенной внутри цилиндра
,
заключенной внутри цилиндра (
(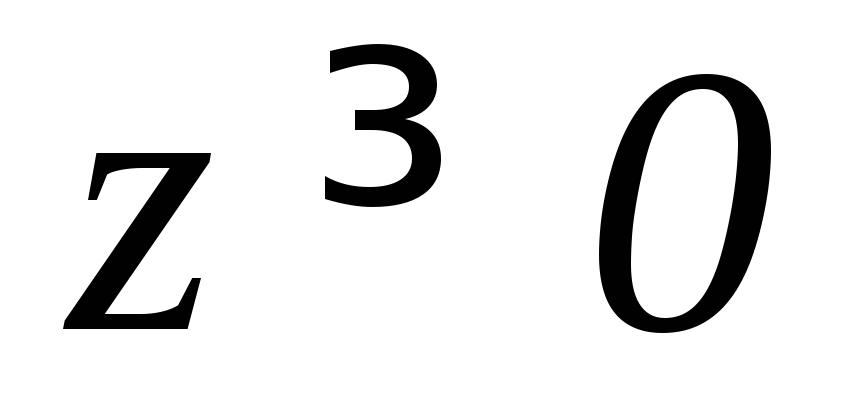 ).
).Поверхности
 ,
вырезанной цилиндром
,
вырезанной цилиндром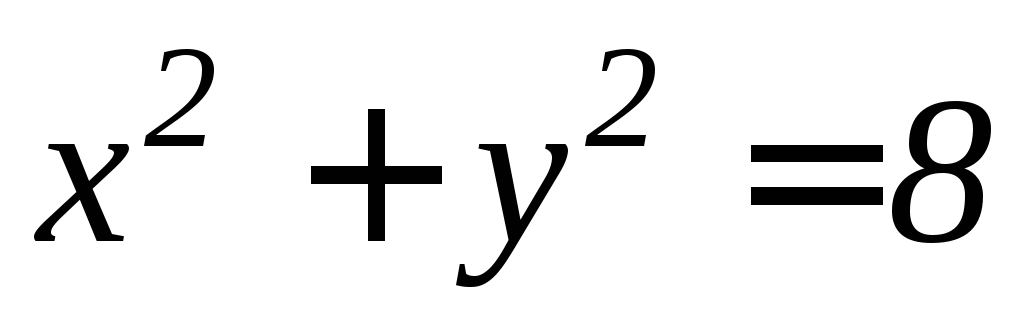 .
.Части сферы
 ,
заключенной внутри цилиндра
,
заключенной внутри цилиндра (
(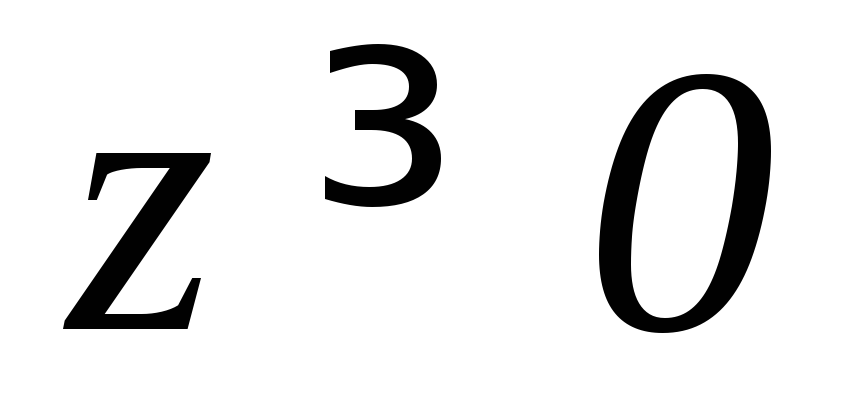 ).
).Поверхности конуса
 ,
отсеченной плоскостями
,
отсеченной плоскостями ,
, (
( ,
,
 ,
, ).
).Поверхности конуса
 ,
расположенной внутри цилиндра
,
расположенной внутри цилиндра .
.Части параболоида
 ,
вырезанной цилиндром
,
вырезанной цилиндром .
.Боковой поверхности конуса
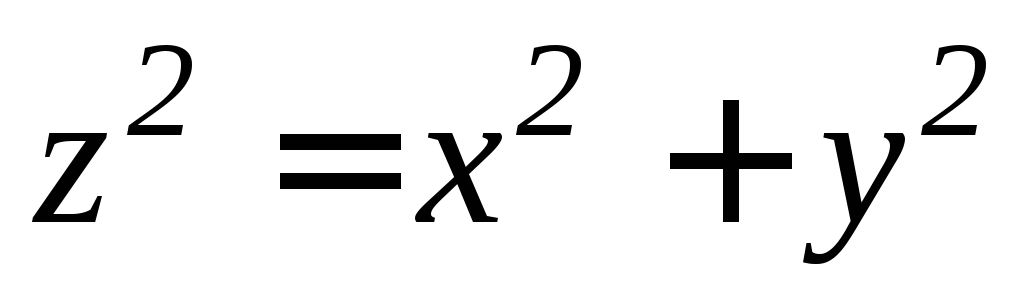 ,
заключенной между плоскостями
,
заключенной между плоскостями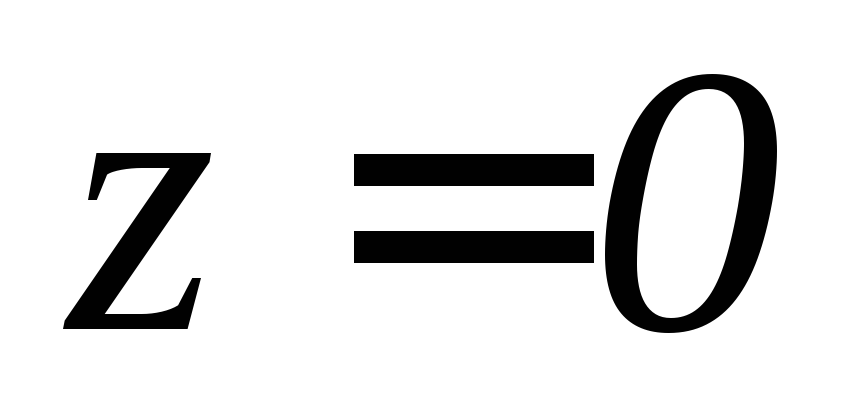 и
и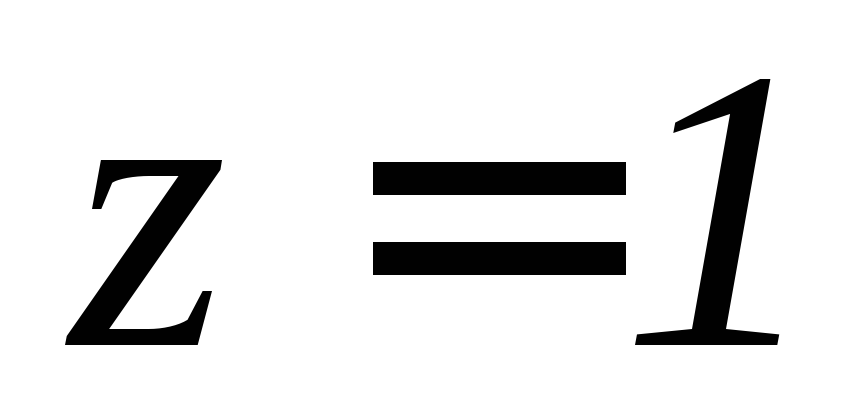 .
.Части параболоида
 ,
вырезанной цилиндром
,
вырезанной цилиндром (
( ,
,
 ,
, ).
).Части сферы
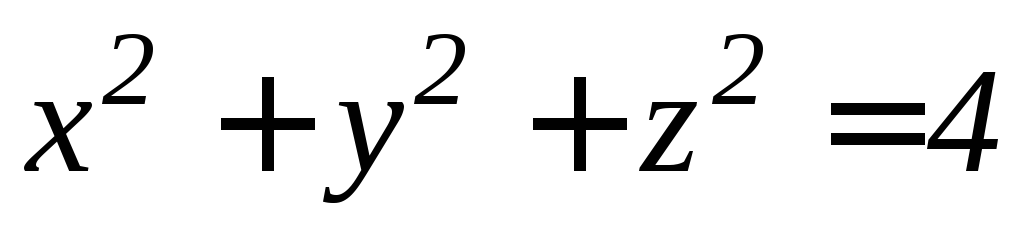 ,
заключенной внутри конуса
,
заключенной внутри конуса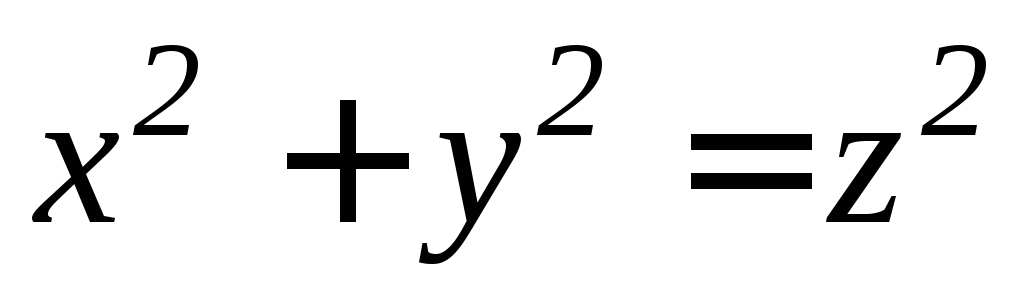 (
( ).
).Поверхности
 ,
расположенной внутри цилиндра
,
расположенной внутри цилиндра .
.Части конуса
 ,
вырезанной цилиндром
,
вырезанной цилиндром (
(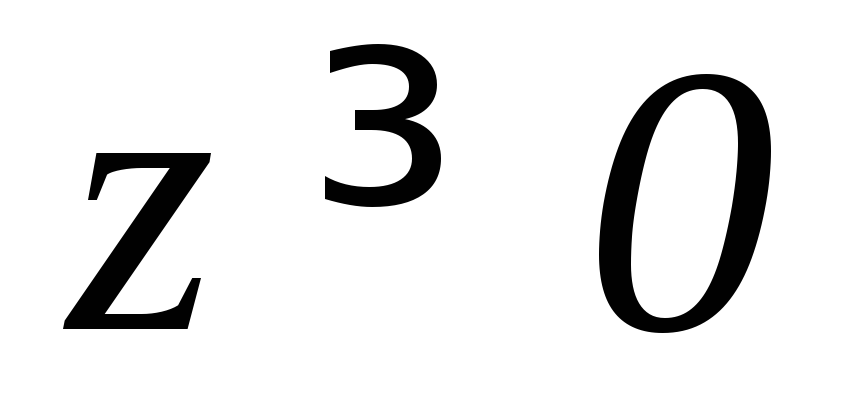 ).
).Части сферы
 ,
вырезанной цилиндром
,
вырезанной цилиндром (
(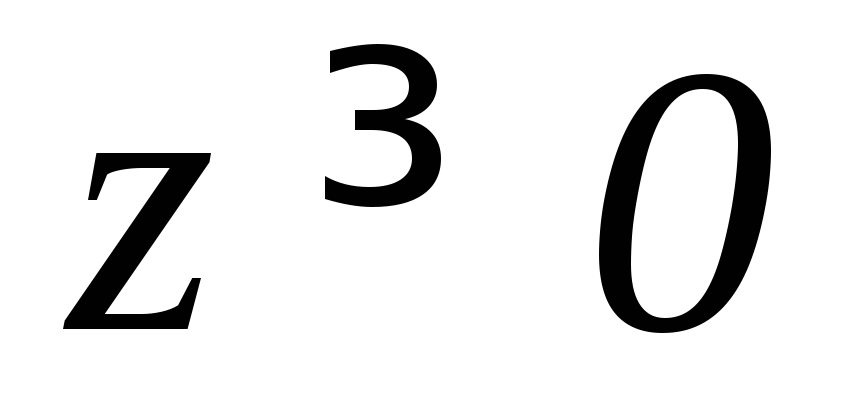 ).
).Поверхности параболоида
 ,
расположенной внутри цилиндра
,
расположенной внутри цилиндра .
.Части плоскости
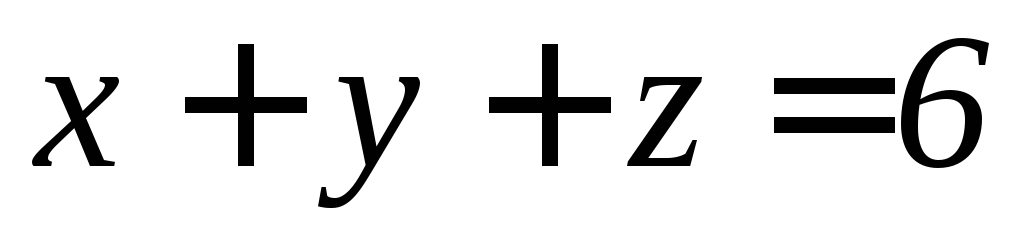 ,
вырезанной цилиндром
,
вырезанной цилиндром .
.Поверхности конуса
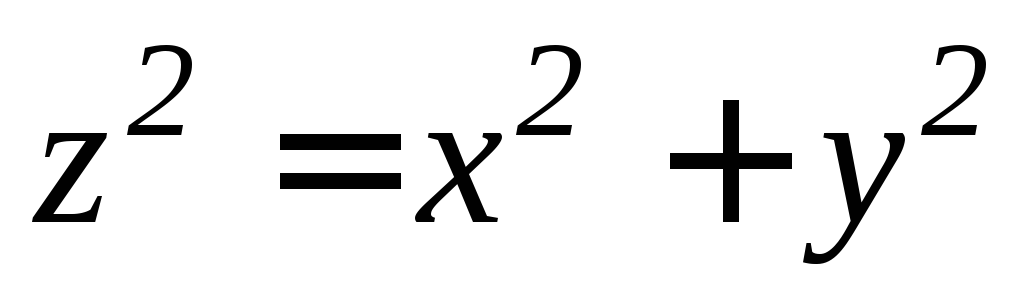 ,
расположенной внутри цилиндра
,
расположенной внутри цилиндра (
( ).
).
Задание 12.7.
Найти массу пластинки плотности
![]() ,
ограниченной заданными линиями:
,
ограниченной заданными линиями:
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
5. |
|
|
6. |
|
|
7. |
|
|
8. |
|
|
9. |
|
|
10. |
|
Найти момент инерции относительно начала координат однородной пластинки, занимающей область, ограниченную заданными линиями:
|
11. |
|
| ||
|
12. |
|
|
|
|
|
13. |
|
|
|
|
Найти координаты центра тяжести однородной пластинки, занимающей область, ограниченную заданными линиями:
|
14. |
|
|
15. |
|
|
16. |
|
|
17. |
|
|
18. |
|
|
19. |
|
|
20. |
|
|
21. |
|
|
22. |
|
| ||
|
23. |
|
|
24. |
|
|
25. |
|
| ||
Задание 12.8.
Вычислить тройные интегралы по областям![]() ,
ограниченным указанными поверхностями:
,
ограниченным указанными поверхностями:
 ,
,
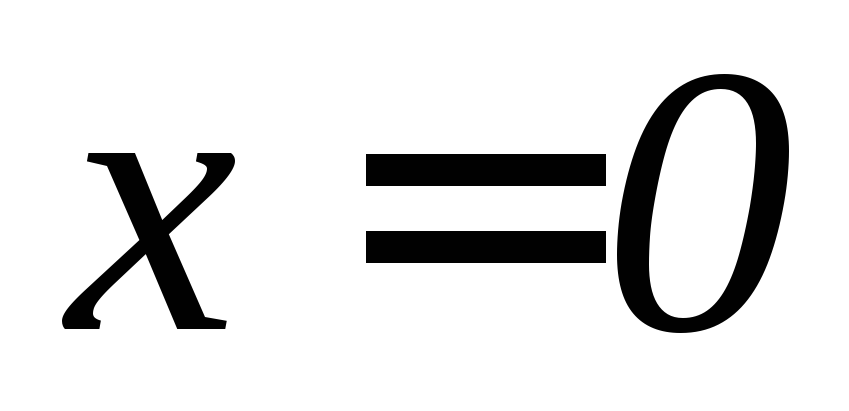 ,
, ,
, ,
,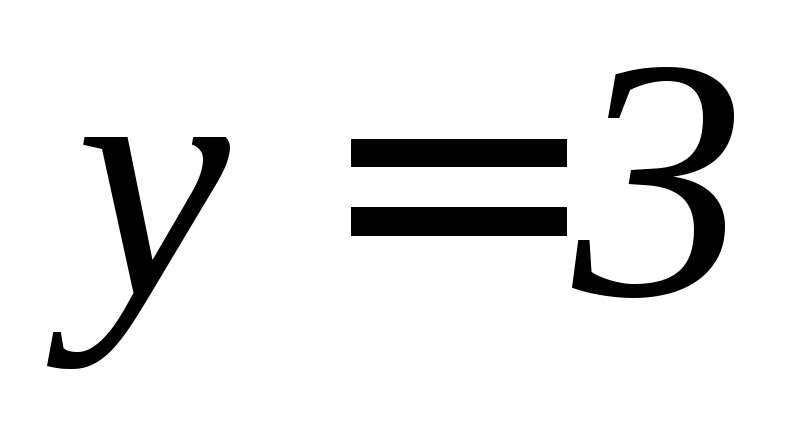 ,
, ,
, .
. ,
,
 ,
, ,
, ,
, ,
,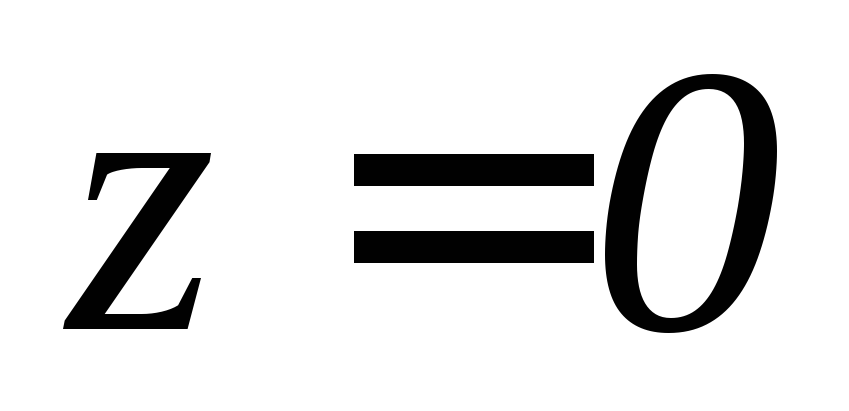 ,
, .
. ,
,
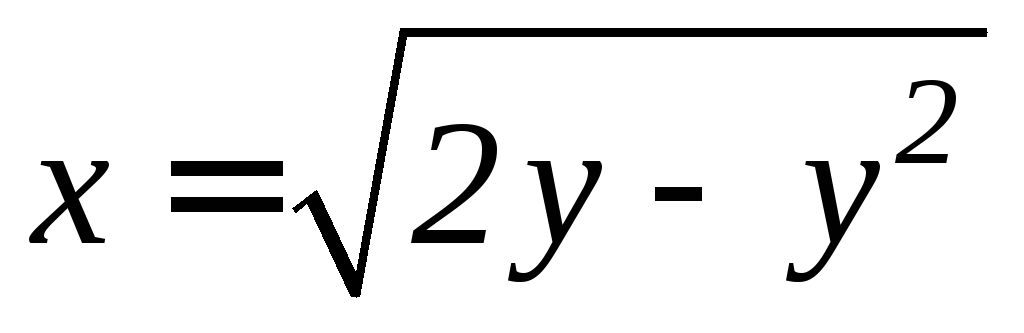 ,
, ,
,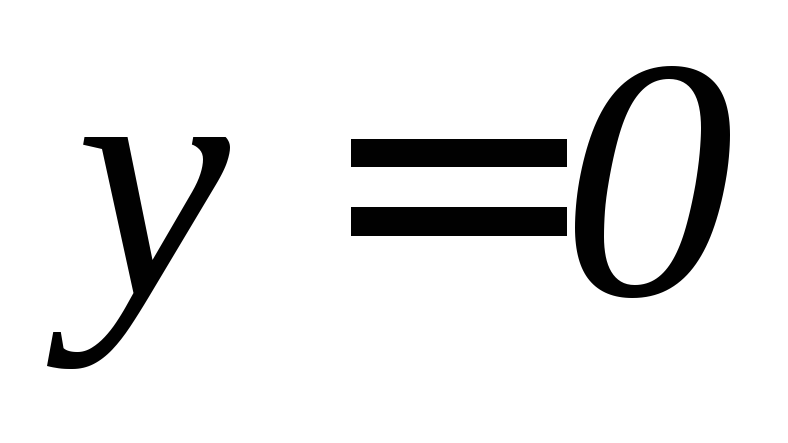 ,
, ,
, ,
, .
. ,
,
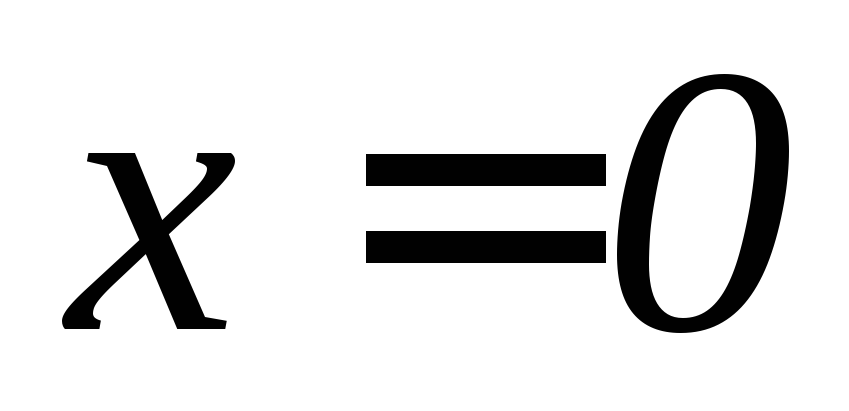 ,
, ,
,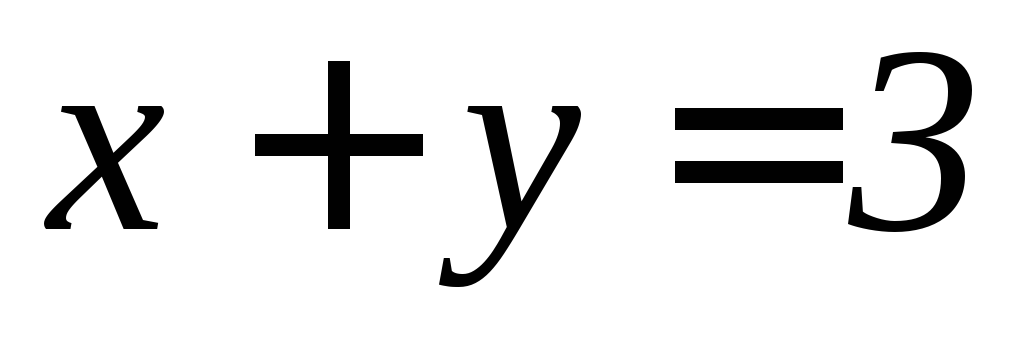 ,
, ,
, .
. ,
,
 ,
, ,
,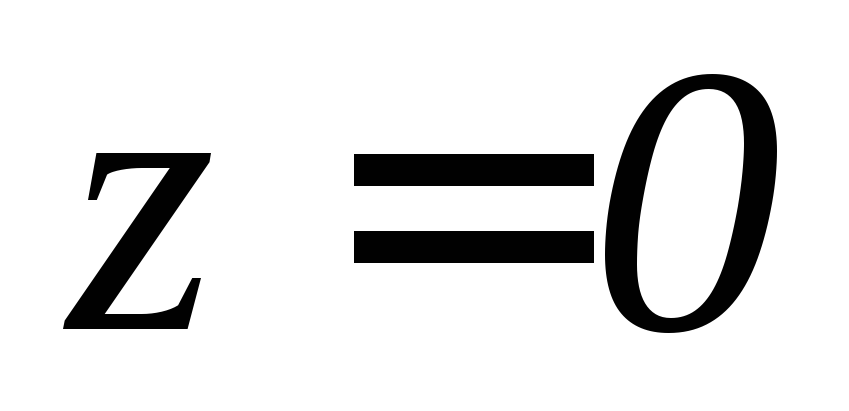 ,
,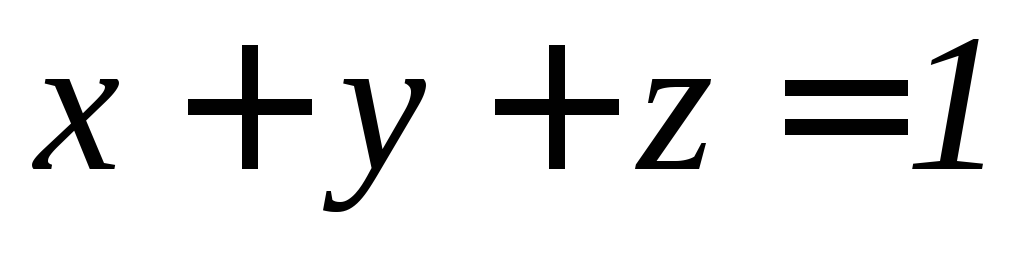 .
. ,
,
 ,
, ,
, ,
,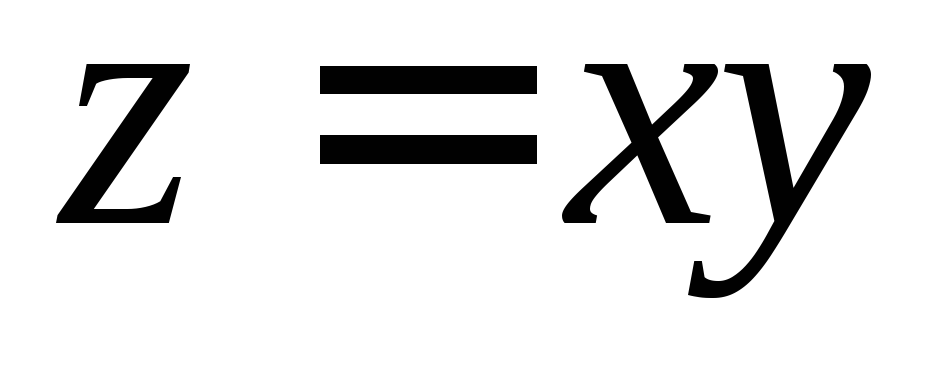 .
.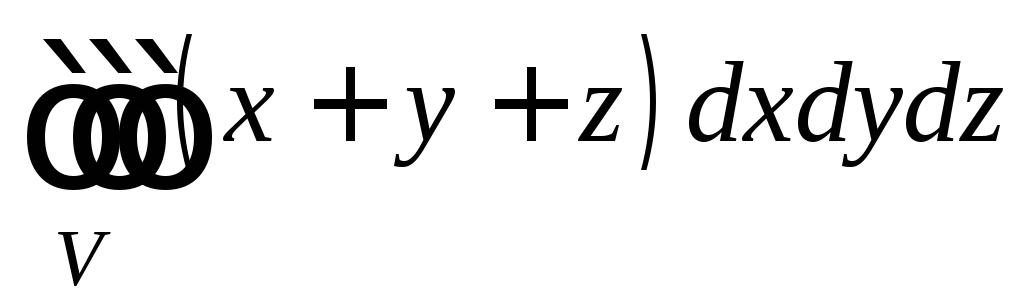 ,
,
 ,
, ,
, ,
, ,
, ,
, .
. ,
,
 ,
,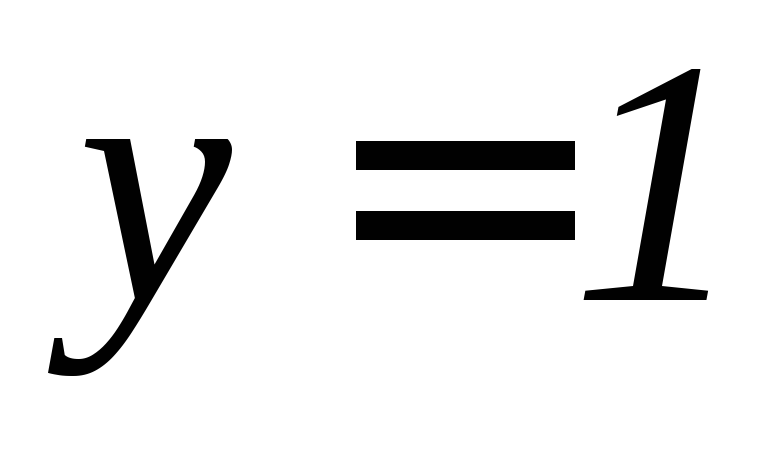 ,
, ,
, .
. ,
,
 ,
, ,
, ,
, ,
, ,
, .
. ,
,
 ,
, ,
, ,
, ,
, ,
, .
. ,
,
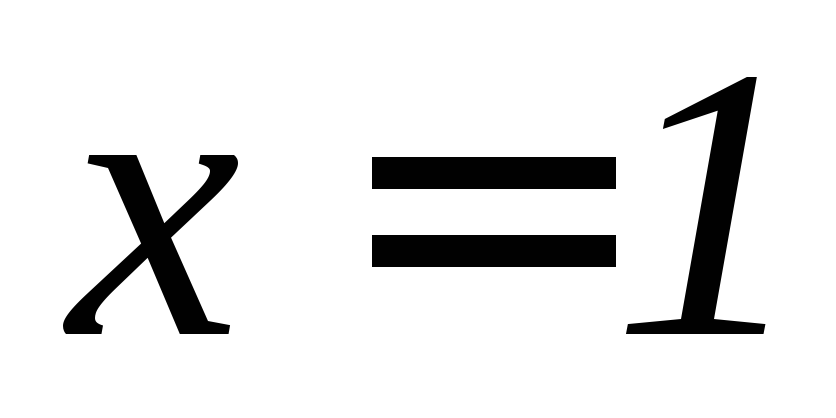 ,
, ,
,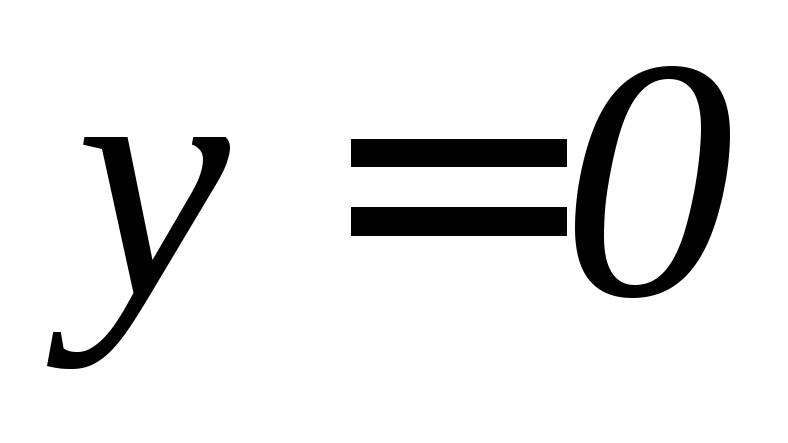 ,
,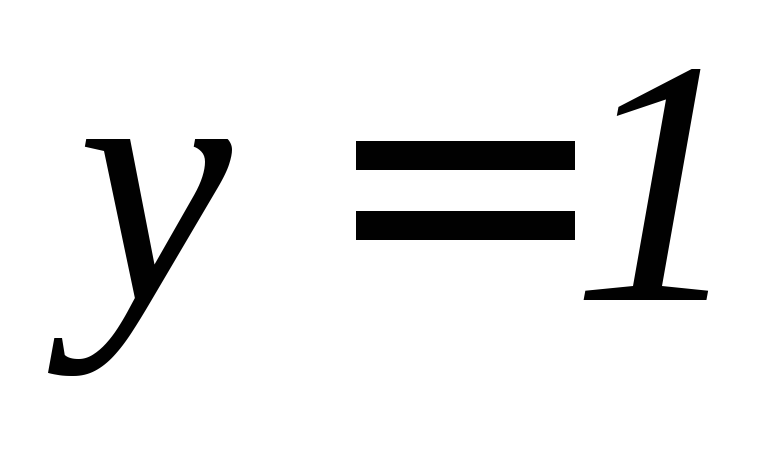 ,
, ,
, .
. ,
,
 ,
, ,
, ,
, ,
, ,
, .
. ,
,
 ,
, ,
, ,
, ,
,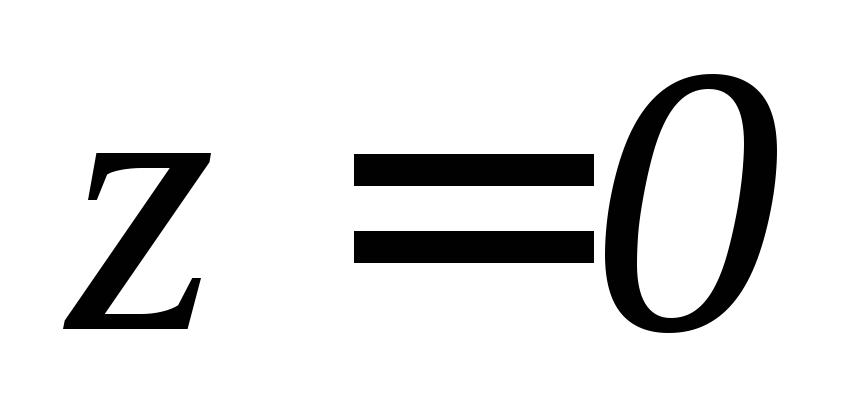 ,
, .
. ,
,
 ,
,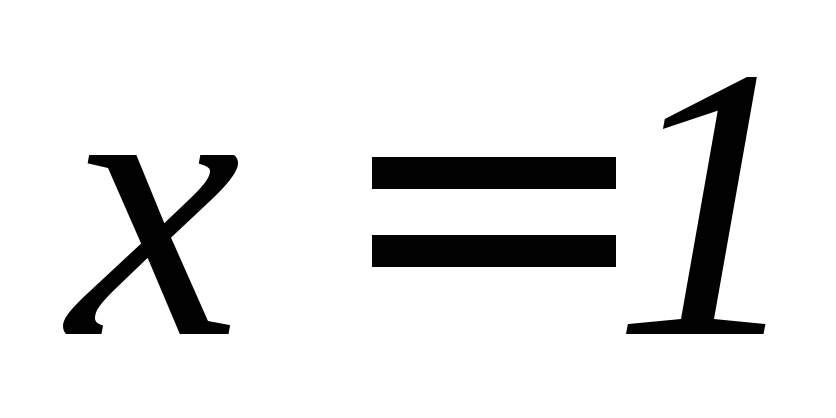 ,
, ,
,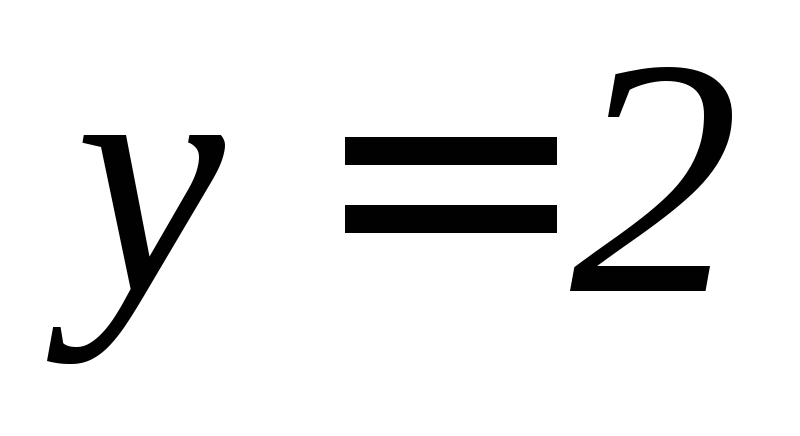 ,
, ,
,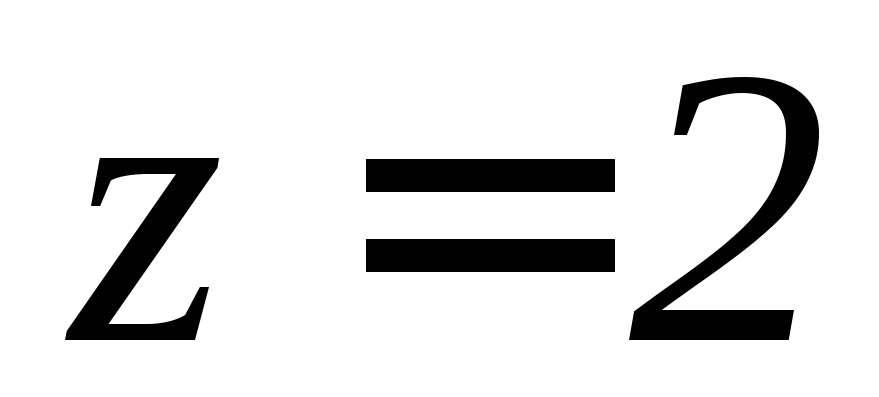 .
. ,
,
 ,
,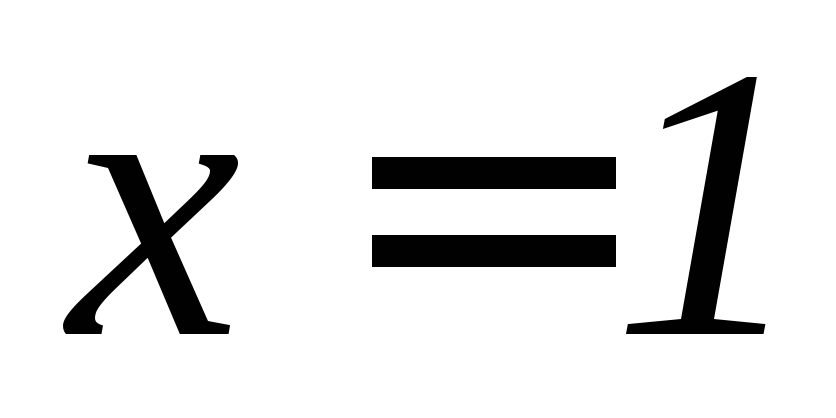 ,
, ,
, ,
, ,
, .
. ,
,
 ,
, ,
, ,
, .
. ,
,
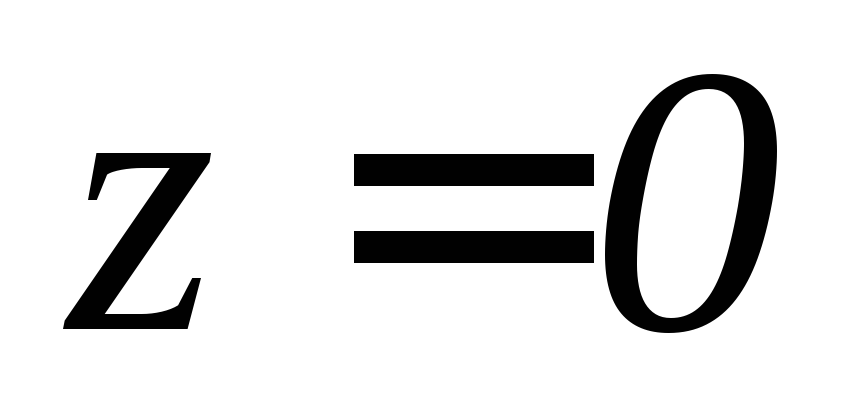 ,
, ,
, ,
, .
. ,
,
 ,
, ,
, ,
, .
. ,
,
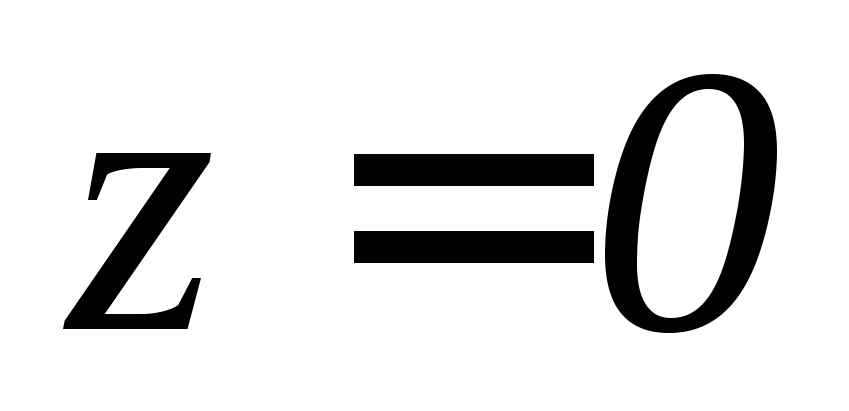 ,
, ,
,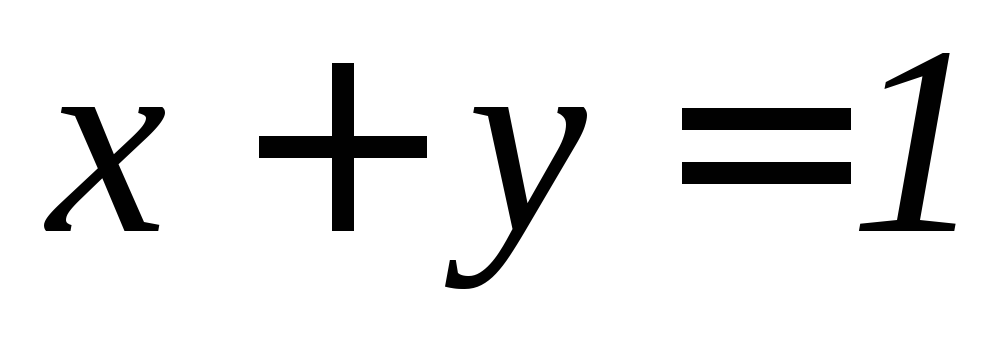 ,
, ,
,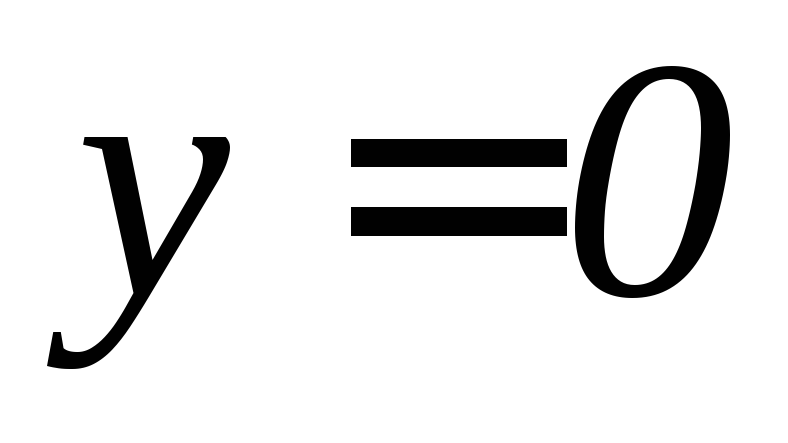 .
. ,
,
 ,
, ,
,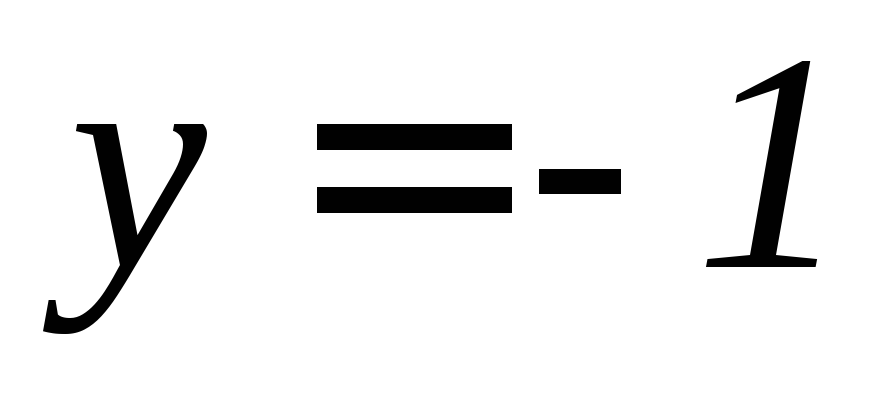 ,
, ,
,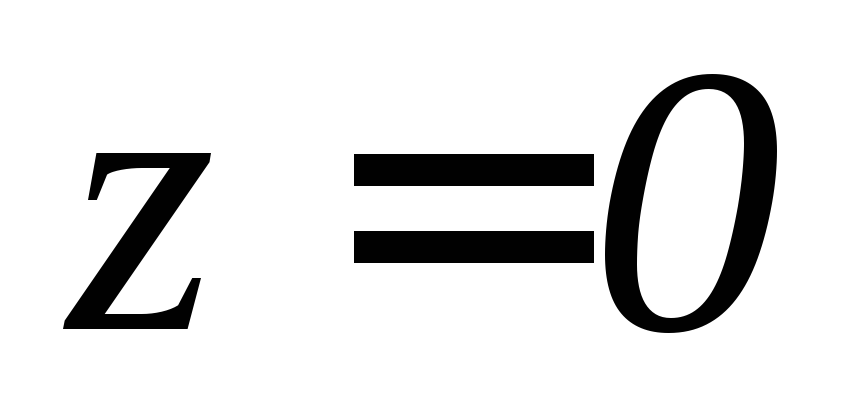 ,
,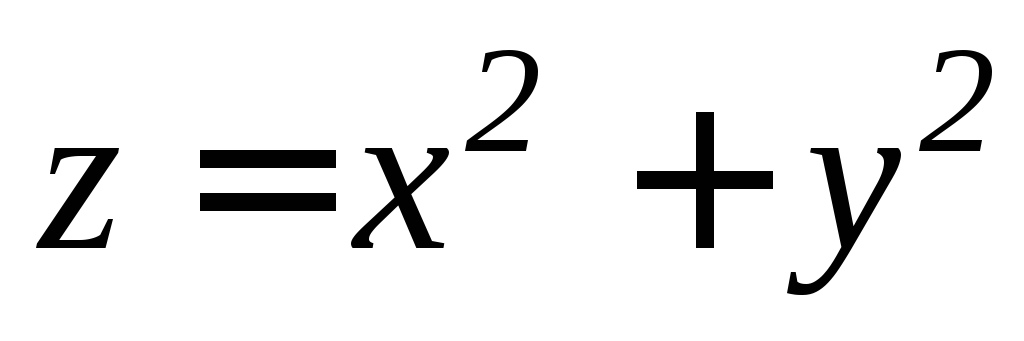 .
.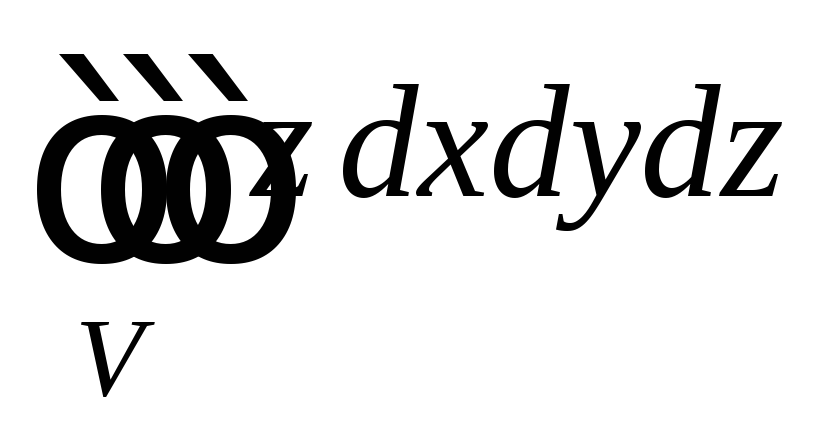 ,
,
 ,
, ,
, ,
,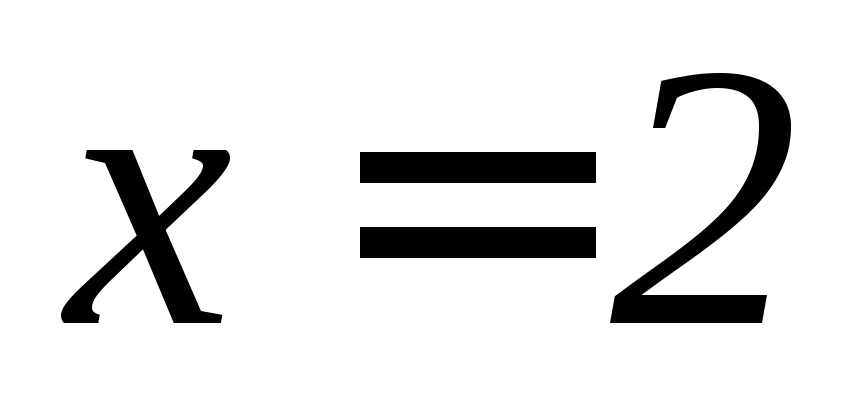 .
.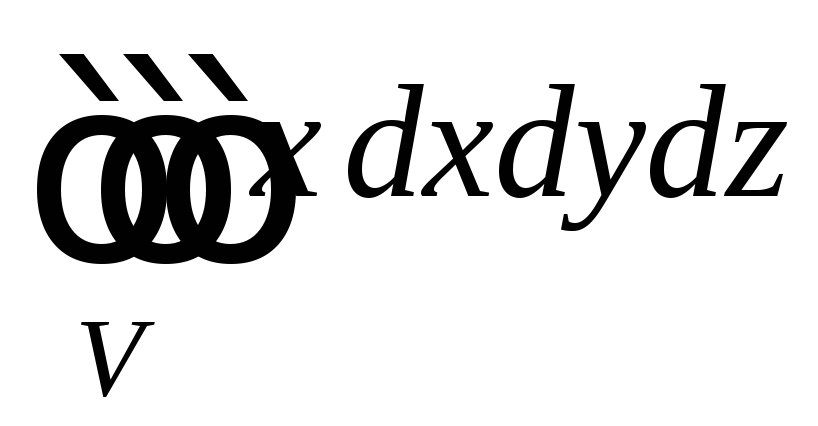 ,
,
 ,
, ,
, ,
, ,
, ,
, .
. ,
,
 ,
, ,
, .
. ,
,
 ,
, ,
, ,
, ,
, ,
, .
. ,
,
 ,
, (
( ,
,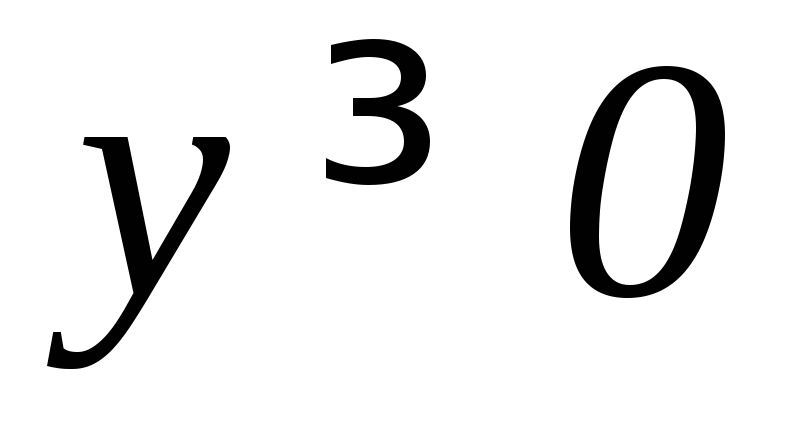 ).
).
Задание 12.9. С помощью тройного интеграла вычислить объем тела, ограниченного заданными поверхностями:
 ,
,
 .
.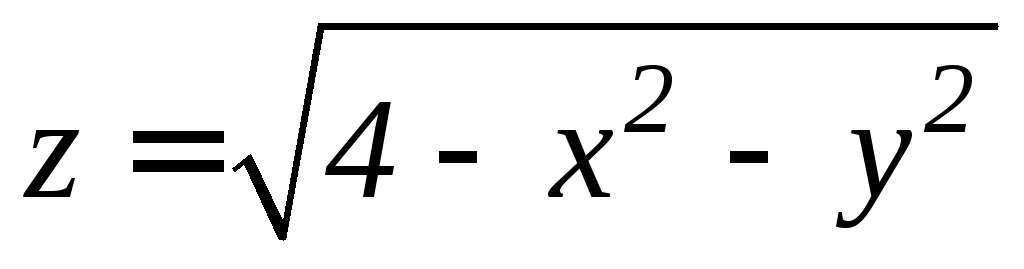 ,
,
 .
.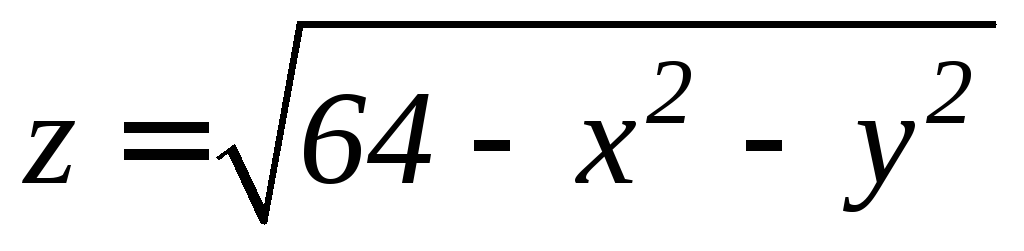 ,
,
 ,
, (внутри цилиндра).
(внутри цилиндра).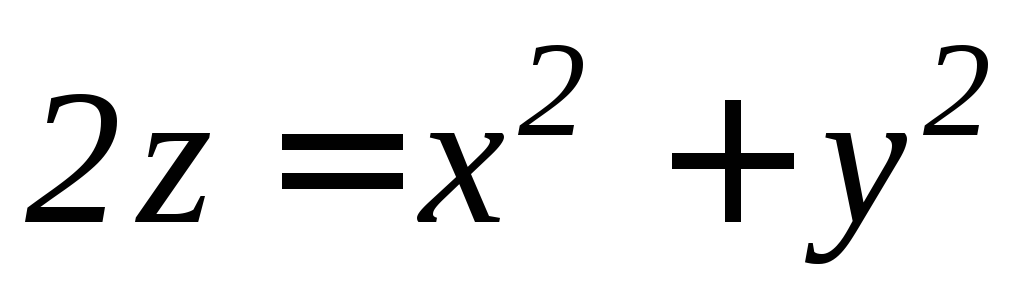 ,
,
 .
. ,
,
 ,
,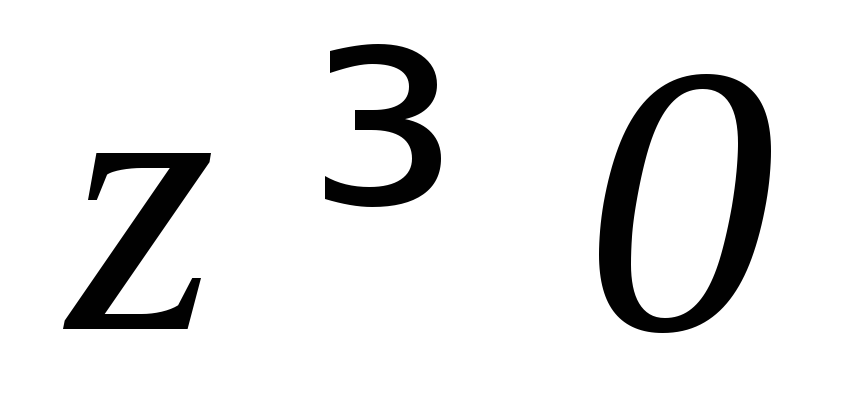 (внутри цилиндра).
(внутри цилиндра). ,
,
 .
. ,
,
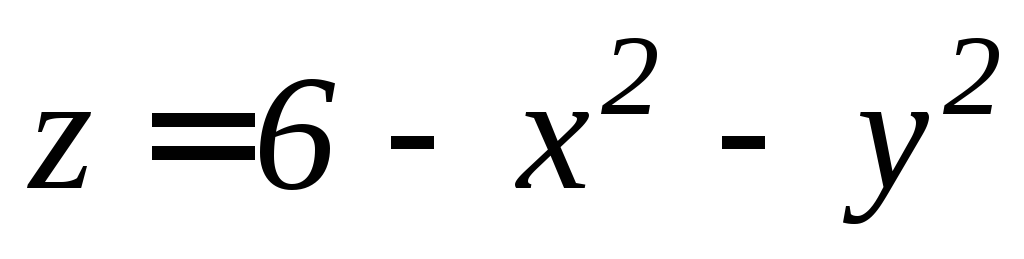 .
. ,
,
 .
. ,
,
 ,
,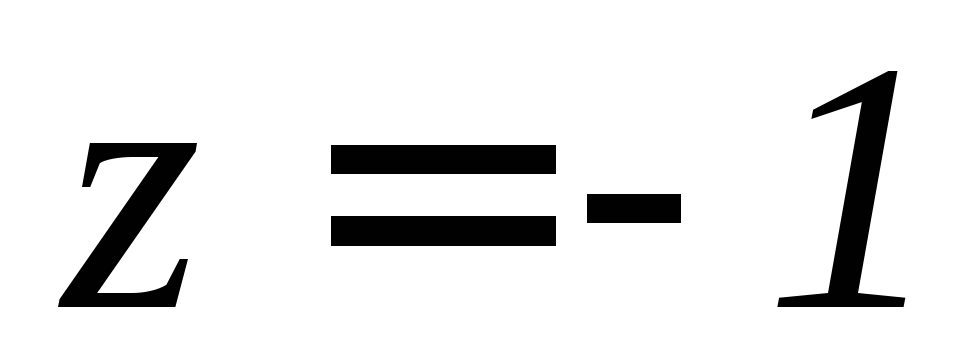 ,
, .
. ,
,
 ,
,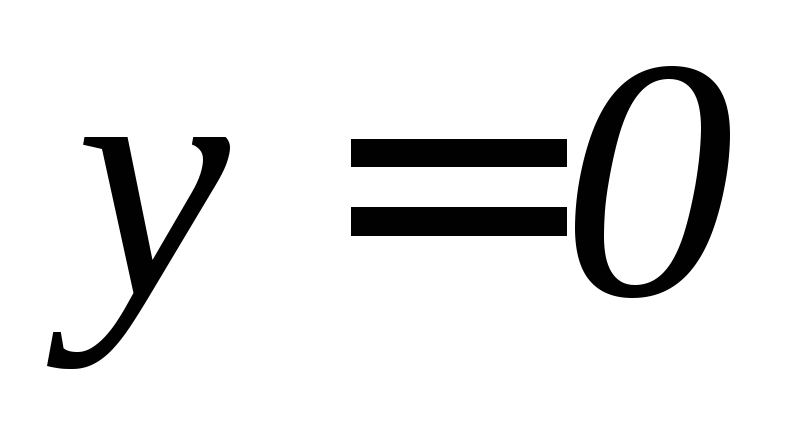 ,
, .
. ,
,
 ,
, ,
, ,
, .
. ,
,
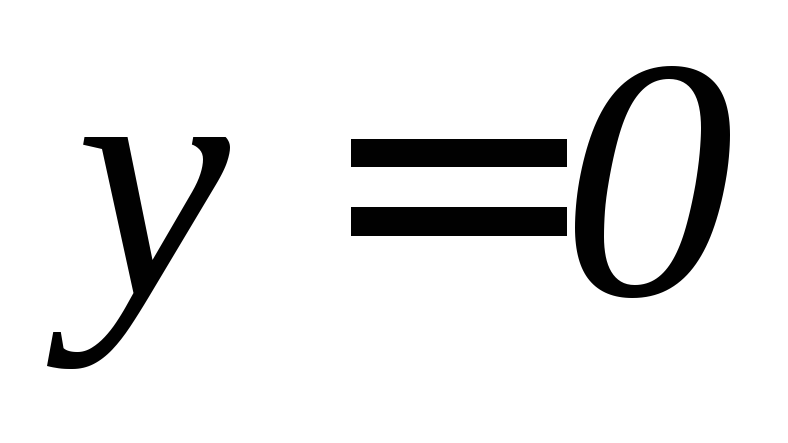 ,
, ,
, .
. ,
,
 .
. ,
,
 ,
,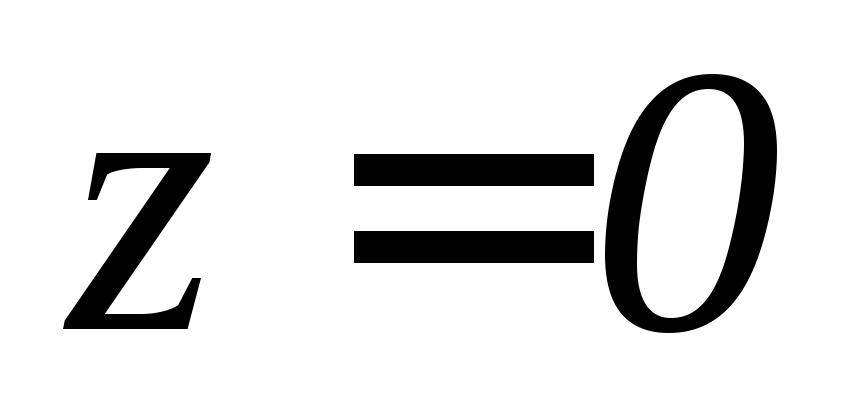 (вне цилиндра).
(вне цилиндра).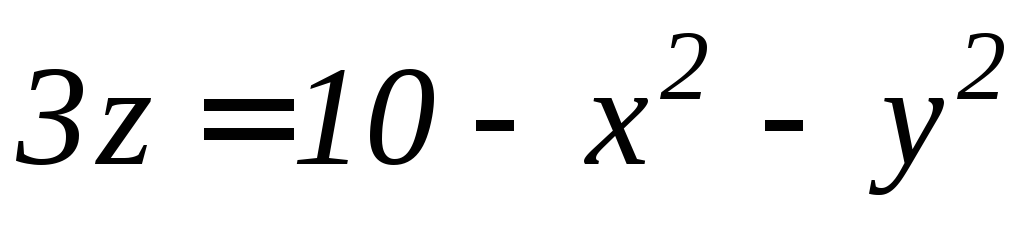 ,
,
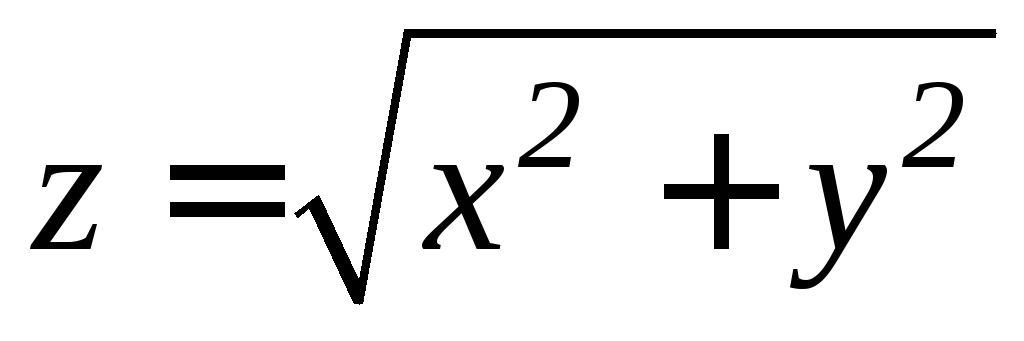 .
.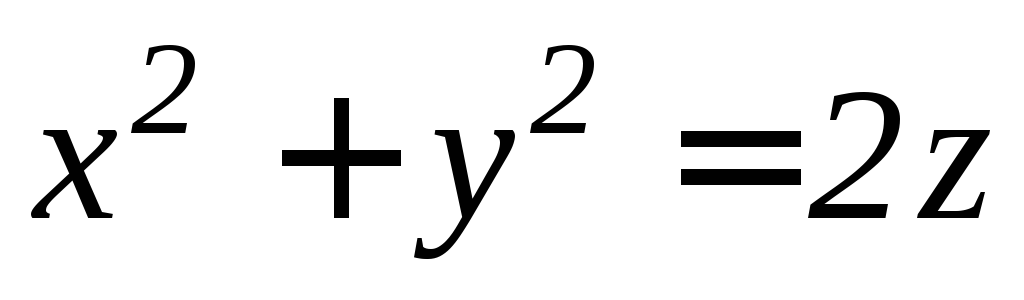 ,
,
 ,
, .
. ,
,
 ,
,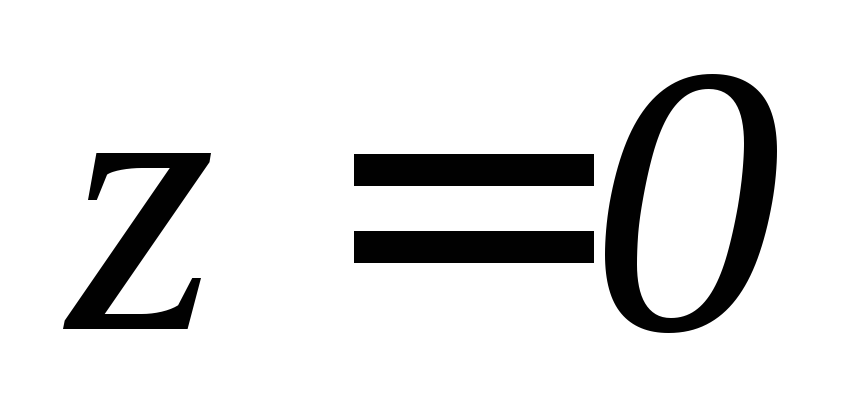 .
. ,
,
 ,
, (внутри цилиндра).
(внутри цилиндра). ,
,
 .
. ,
,
 (внутри параболоида).
(внутри параболоида). ,
,
 .
. ,
,
 .
. ,
,
 .
. ,
,
 ,
,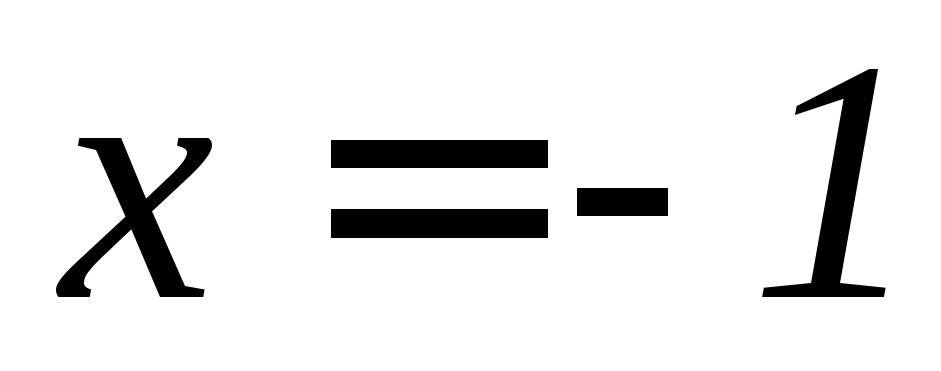 ,
, .
. ,
,
 ,
, ,
, ,
, .
.
Задание 12.10. Найти координаты центра тяжести однородного тела, занимающей область, ограниченную заданными поверхностями:
|
1. |
|
|
|
| |
|
2. |
|
|
|
| |
|
3. |
|
|
|
| |
|
4. |
|
|
| ||
|
5. |
|
|
| ||
|
6. |
| ||||
|
7. |
| ||||
|
8. |
| ||||
|
9. |
| ||||
|
10. |
| ||||
Найти момент
инерции относительно оси
![]() однородного тела, ограниченного
заданными поверхностями:
однородного тела, ограниченного
заданными поверхностями:
|
11. |
|
|
|
|
12. |
|
|
|
Найти момент
инерции относительно оси
![]() однородного тела, ограниченного заданными
поверхностями:
однородного тела, ограниченного заданными
поверхностями:
|
13. |
|
|
|
Найти массу тела
с объемной плотностью
![]() ,
ограниченного заданными поверхностями:
,
ограниченного заданными поверхностями:
 ,
,
 ,
, ,
, ,
, ,
, ,
, .
. ,
,
 ,
,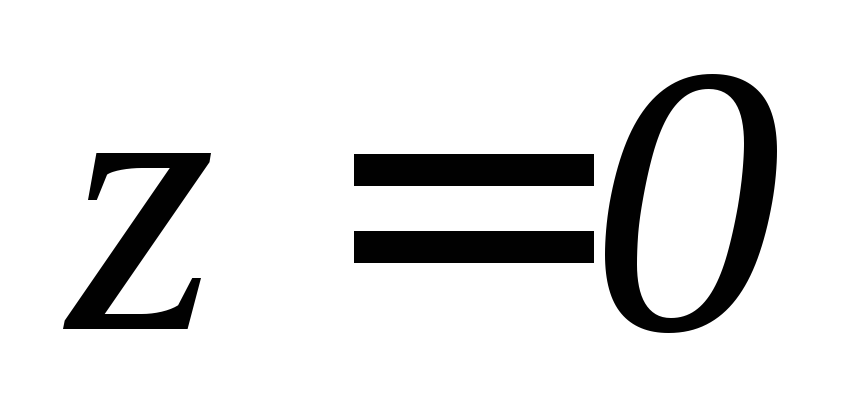 ,
, .
. ,
,
 ,
, ,
, ,
,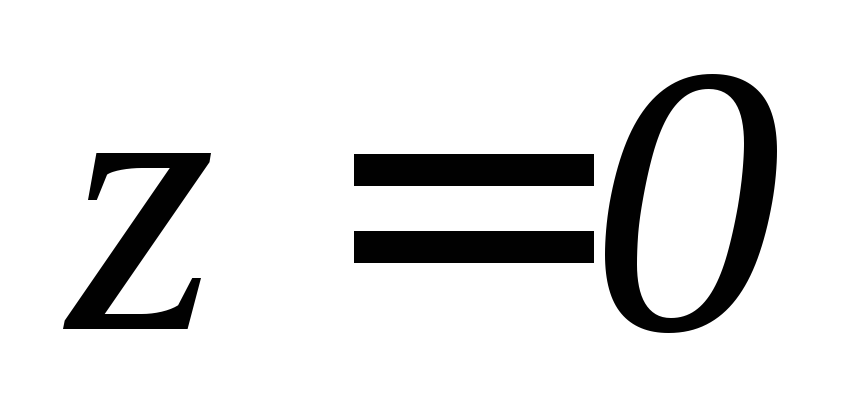 ,
, .
. ,
,
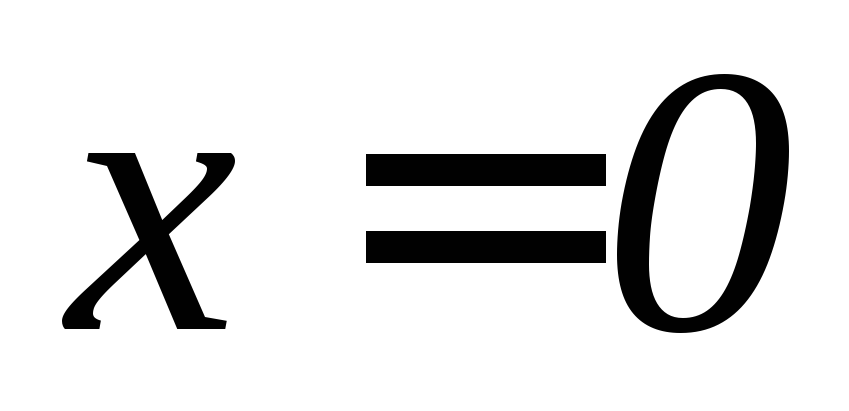 ,
,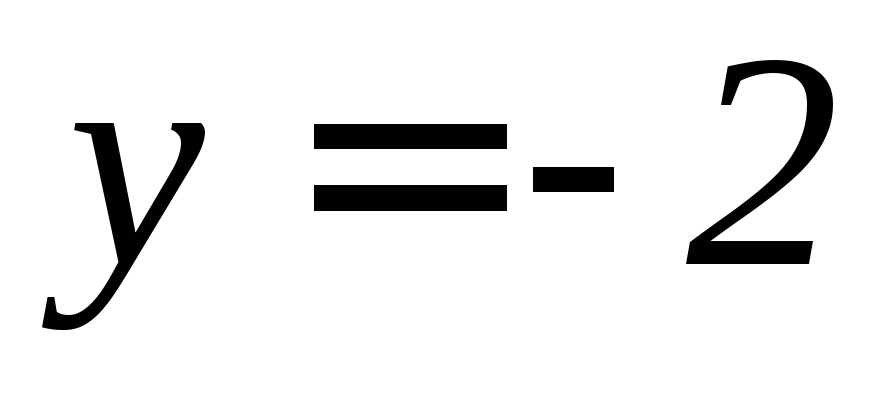 ,
,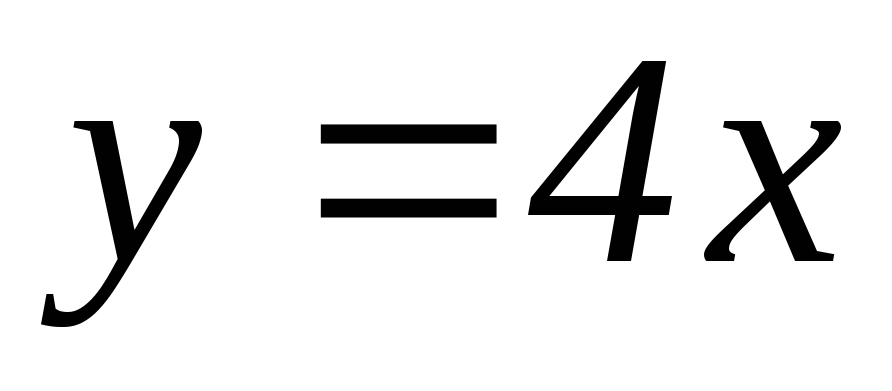 ,
, ,
, .
. ,
,
 ,
,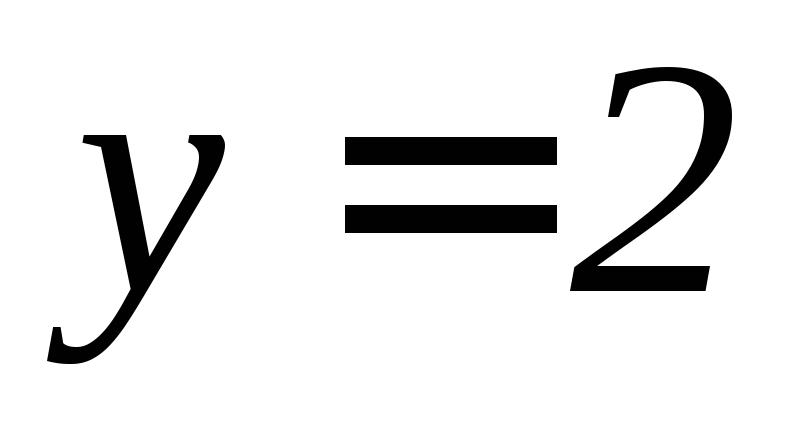 ,
, ,
, ,
, .
. ,
,
 ,
, ,
, ,
, (
( ,
, ).
). ,
,
 ,
, ,
, (
( ,
,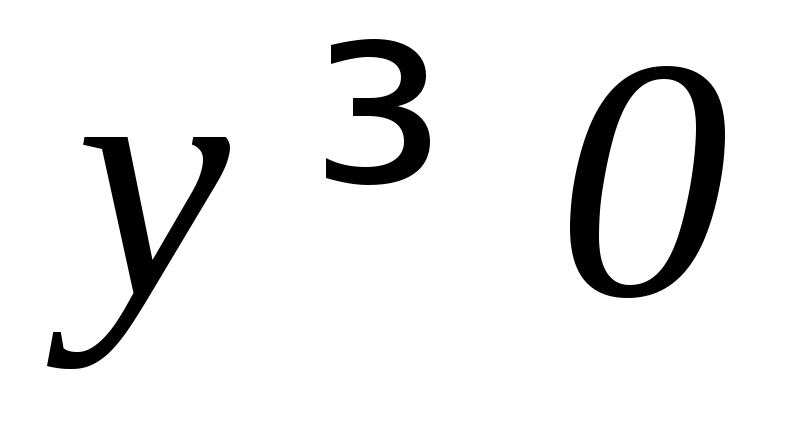 ).
). ,
,
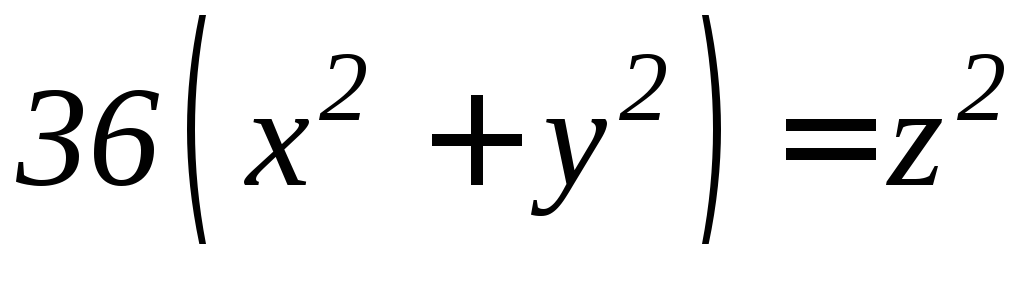 ,
, (
( ,
, ).
).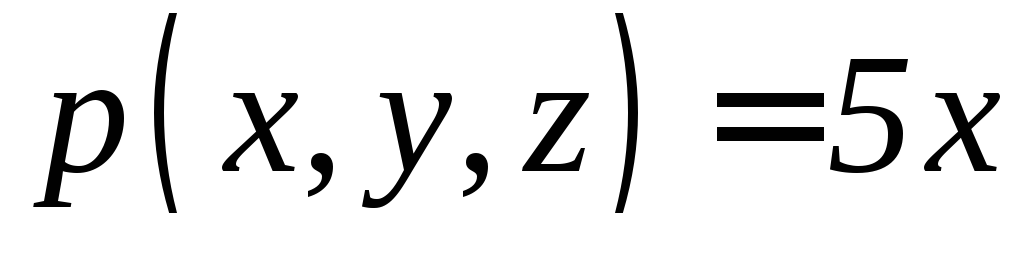 ,
,
 ,
, ,
, (
( ,
, ).
).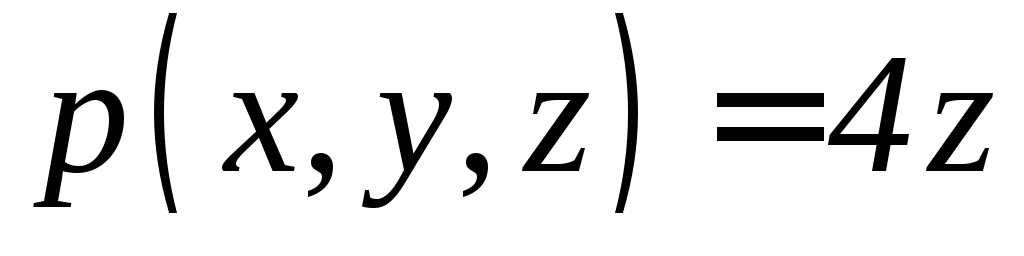 ,
,
 ,
, ,
,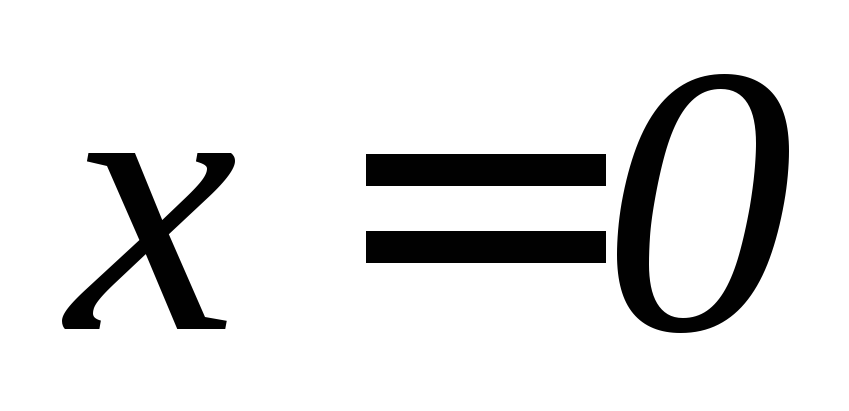 (
( ,
, ).
). ,
,
 ,
,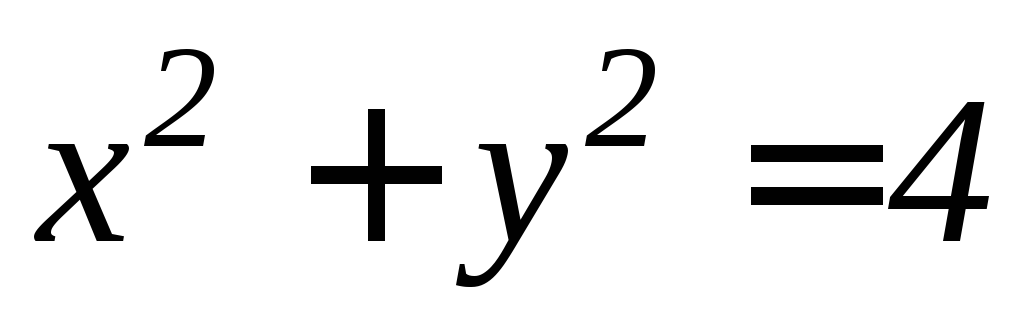 (
( ).
).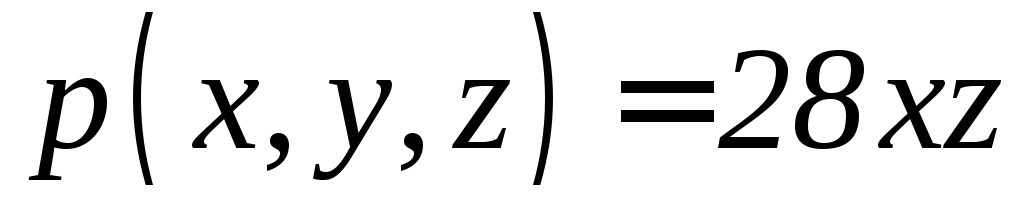 ,
,
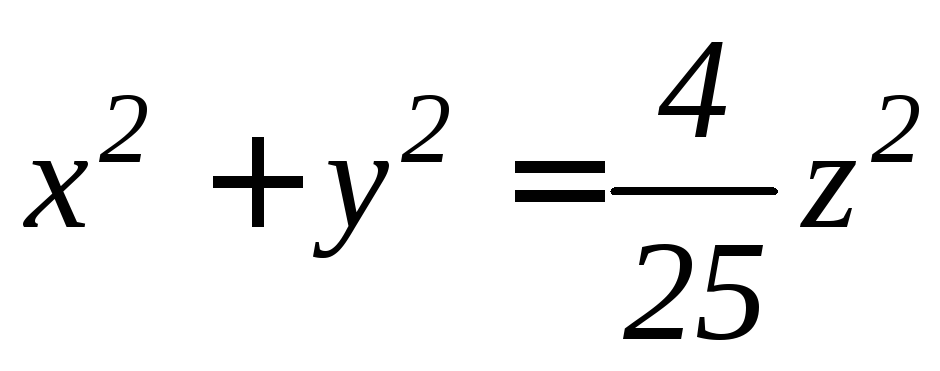 ,
, (
(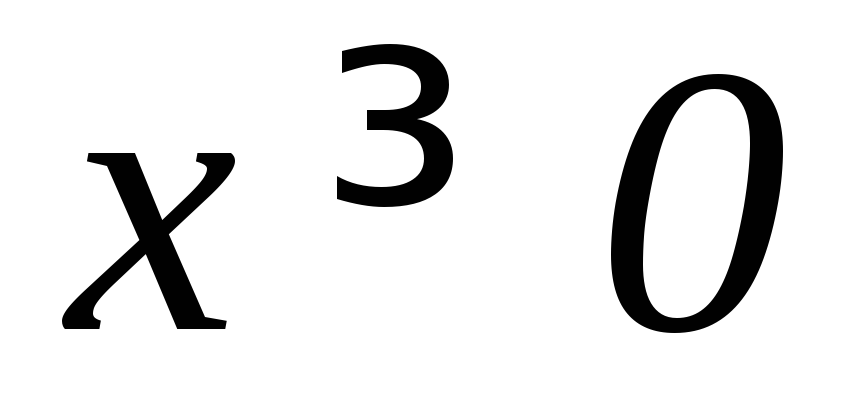 ,
, ).
).
Диаметром области называется наибольшее из расстояний между двумя точками границы этой области



 .
. .
.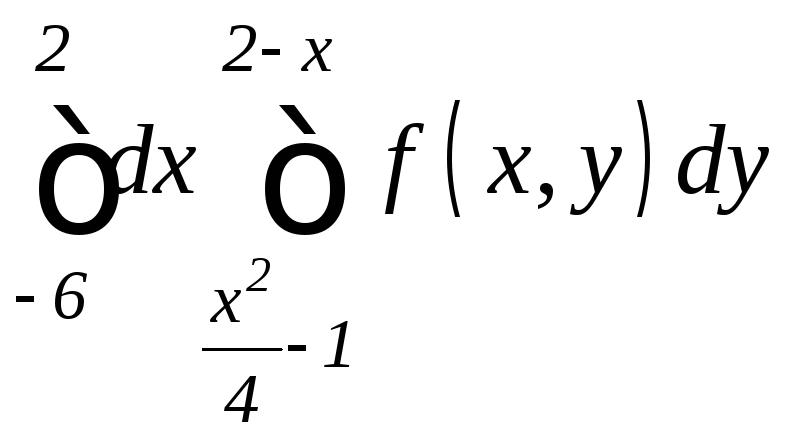 .
. .
.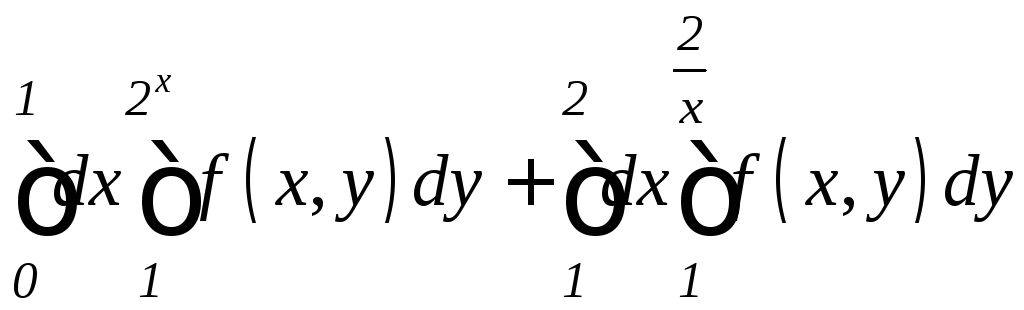 .
. .
.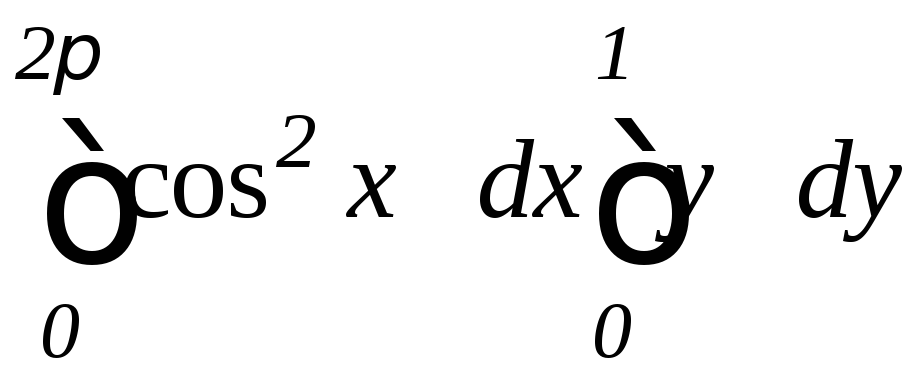 .
. .
. ,
,
 .
. .
. .
. .
. .
. .
.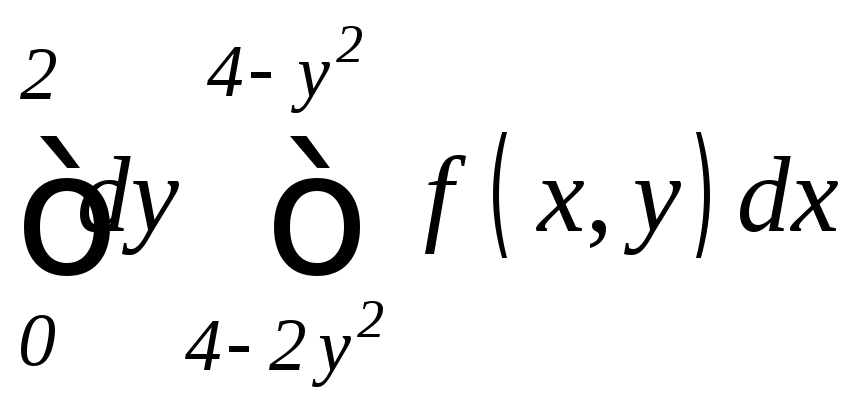 .
. .
. .
.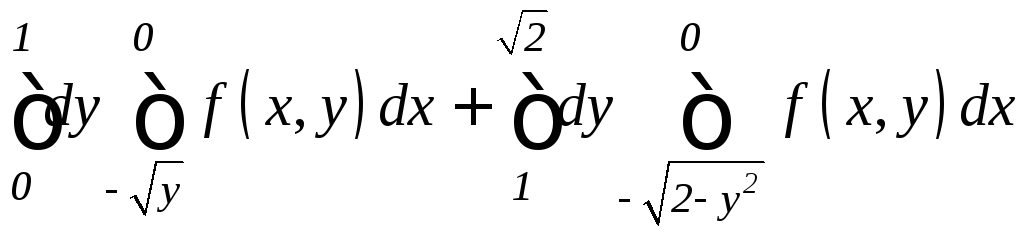 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.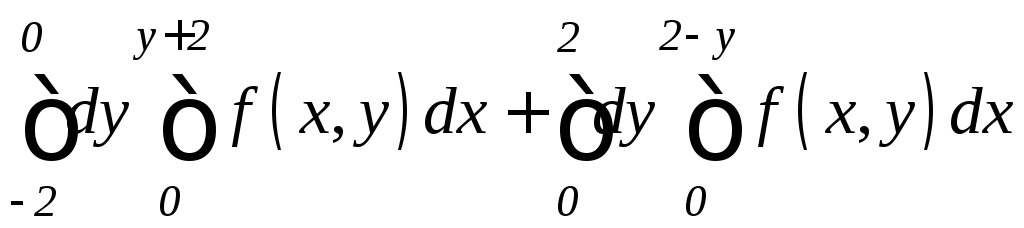 .
. .
. .
.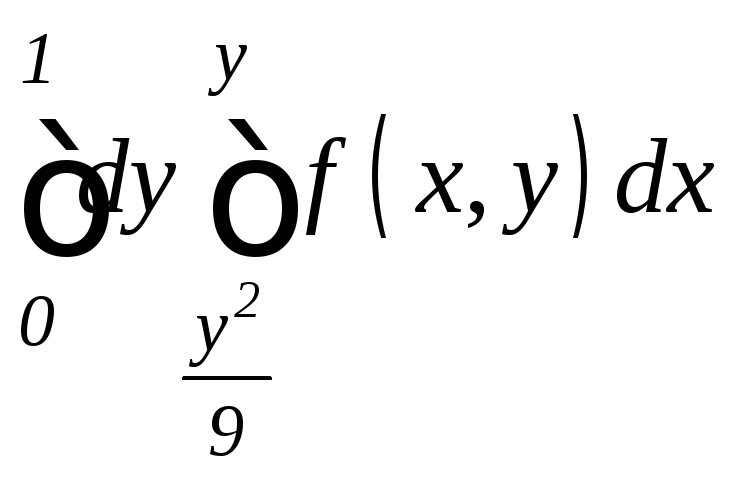 .
.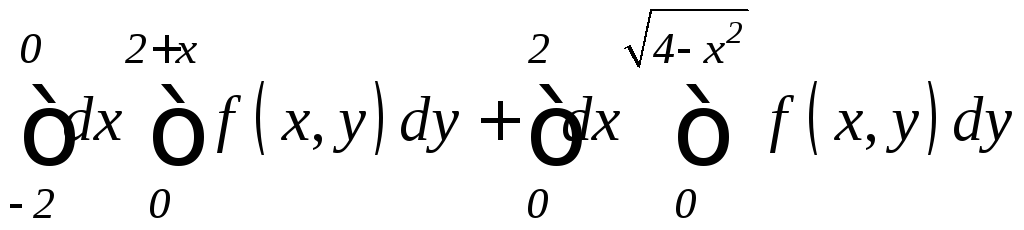 .
.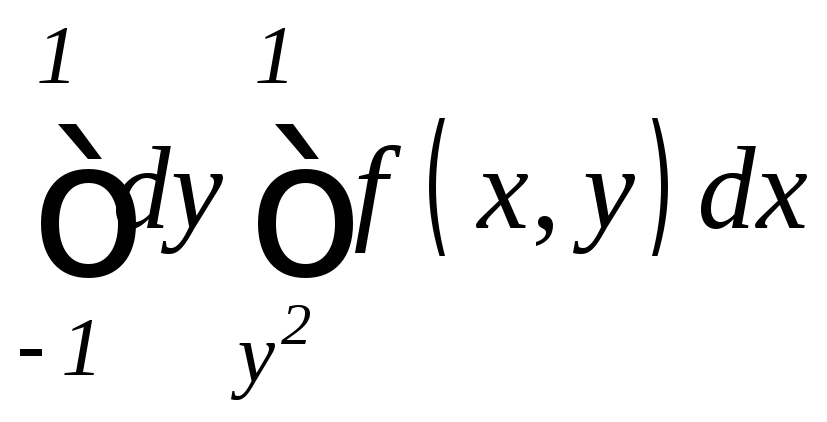 .
. .
.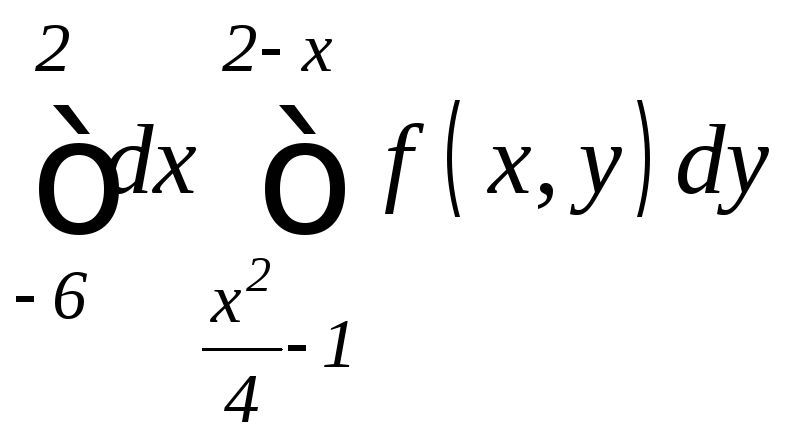 .
. .
. .
. .
.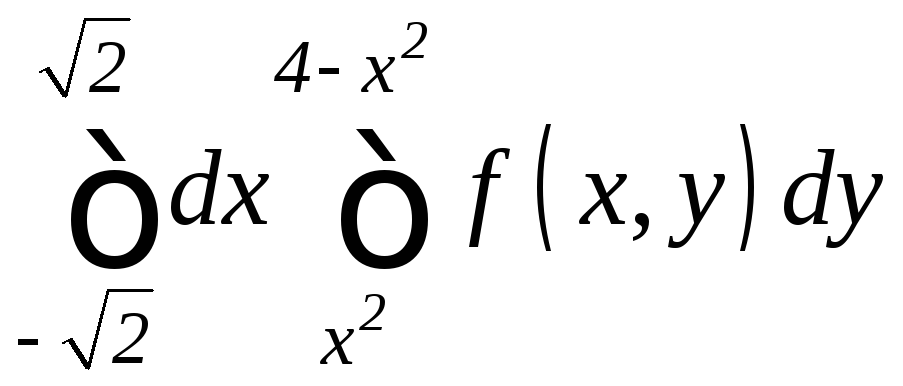 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.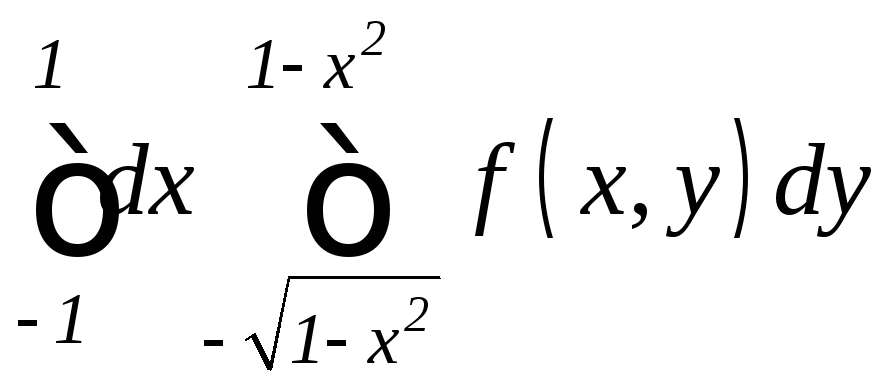 .
. .
. .
. .
. .
. .
. .
. ,
,
 ,
,
 (
(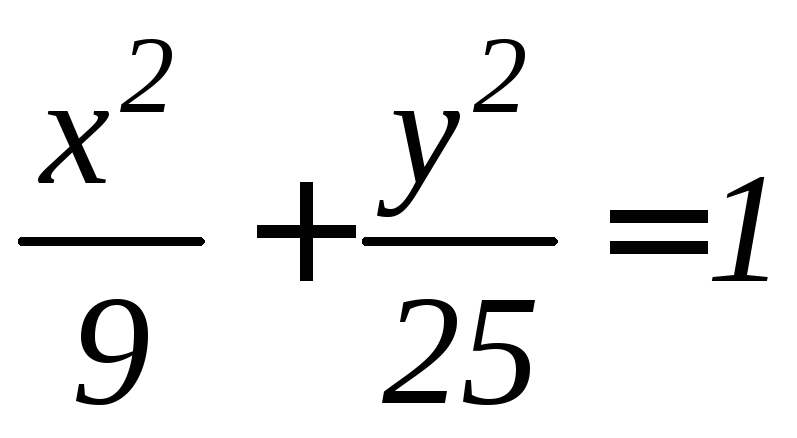 (
( ,
,
 ,
,