Решение. Непосредственное вычисление данного интеграла было бы затруднительным. Однако простая замена переменных

,

позволяет значительно упростить решение. Прямые ив системе координатпереходят в прямыеина плоскости; прямые жеипереходят в прямыеи. Следовательно, заданная областьпреобразуется в прямоугольник(рис. 12.6).

Рис. 12.5	Рис. 12.6

Вычислим якобиан этого преобразования. Для этого выразим ичерези:

, .

Следовательно,

.

По формуле (12.3) окончательно получаем

.

Пример 4. Вычислить , где область- круг.

Решение. Применив формулу (12.4), перейдем к полярным координатам:

.

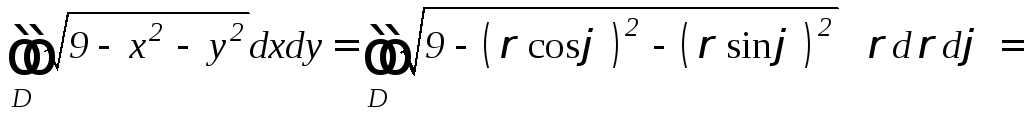
Рис. 12.7

Область в полярной системе координат определяется неравенствами (рис. 12.7),. Таким образом, область- круг – преобразуется в область- прямоугольник. Поэтому имеем:

.

Для вычисления площади плоской фигуры, ограниченной областьюв декартовых координатах используется формула

, или, в полярных координатах .

Рис.12.8

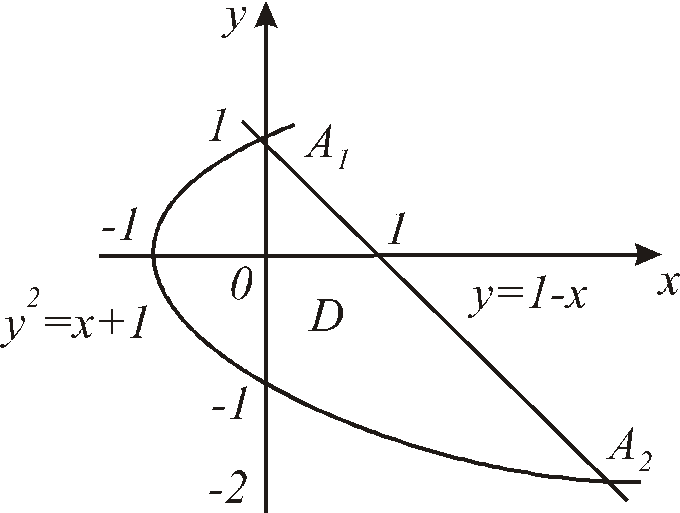
Пример 5. Вычислить площадь области , ограниченной линиями,(рис. 12.8).

Решение. Область представляет собой фигуру, ограниченную слева параболой, справа прямой. Решая систему уравнений

находим точки их пересечения: ,. Следовательно, искомая площадь

.

Объем тела, ограниченного сверху непрерывной поверхностью, снизу плоскостьюи сбоку цилиндрической поверхностью, вырезающей на плоскостиобласть, находится по формуле

Рис. 12.9

.

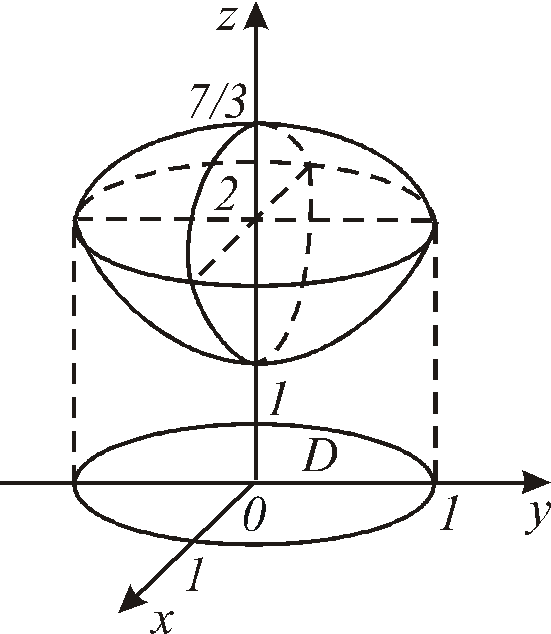
Пример 6. Найти объем тела, ограниченного поверхностями и.

Решение. Данное тело ограничено двумя параболоидами (рис. 12.9). Решая систему уравнений

находим уравнение линии их пересечения: ,.

Искомый объем равен разности объемов двух цилиндрических тел с одним основанием (круг ) и ограниченных сверху соответственно поверхностямии:

.

Переходя к полярным координатам и пользуясь формулой (12.4), находим:

.

Если гладкая поверхность задана уравнением , а ее проекция на плоскостьесть область, в которой,и- непрерывные функции, топлощадь поверхности вычисляется по формуле

.

Рис. 12.10

Пример 7. Вычислить площадь части поверхности полусферы (), вырезанной цилиндром(рис. 12.10).

Решение. Уравнение поверхности имеет вид , областьесть круг, ограниченный окружностью. Находим производные

, .

Искомая площадь: .

Для вычисления двойного интеграла перейдем к полярным координатам. Уравнение окружности примет вид при. Следовательно,

.

Масса плоской пластинки с переменной плотностью распределения массынаходится по формуле

.

В случае однородной пластинки .

Статические моменты области относительно осейивычисляются по формулам

и ;

а координаты центра тяжести – по формулам

и .

Рис. 12.11

Пример 8. Найти координаты центра тяжести равнобедренного треугольника, если плотность распределения массы равна (рис. 12.11).

Решение. Находим массу и статические моменты:

;

;

.

Отсюда координаты центра тяжести:

; .

Моменты инерции пластинки относительно осей имогут быть найдены по формулам

и .

Момент инерции фигуры относительно начала координат – по формуле

.

Рис.12.12

Пример 9. Найти моменты инерции относительно начала координат однородной фигуры, ограниченной линиями ,,(рис. 12.12).

Решение. Момент инерции относительно начала координат равен

.

12.2. Тройной интеграл

Предел интегральной суммы при стремлении к нулю наибольшего из диаметров всех элементарных областей называется тройным интегралом от функции по областии обозначается следующим образом:

.

Пусть область определяется неравенствами,,, где,,,- непрерывные функции. Тогда тройной интеграл от функциипо областивычисляется по формуле

. (12.5)

Рис. 12.13

Пример 10. Вычислить интеграл , где- пирамида, ограниченная плоскостьюи координатными плоскостями,,(рис. 12.13).