
- •12. Кратные интегралы
- •12.1. Двойной интеграл
- •Решение. Непосредственное вычисление данного интеграла было бы затруднительным. Однако простая замена переменных
- •Решение. Применив формулу (12.4), перейдем к полярным координатам:
- •Решение. Область представляет собой фигуру, ограниченную слева параболой, справа прямой. Решая систему уравнений
- •Решение. Данное тело ограничено двумя параболоидами (рис. 12.9). Решая систему уравнений
- •Решение. Уравнение поверхности имеет вид , областьесть круг, ограниченный окружностью. Находим производные
- •Решение. Находим массу и статические моменты:
- •Решение. Момент инерции относительно начала координат равен
- •12.2. Тройной интеграл
- •Решение. Область проецируется на плоскостьв треугольник, ограниченный прямыми,,. По формуле (12.5) имеем
- •Решение. Данное тело ограничено сверху плоскостью , снизу – параболоидом(рис. 12.18). Объем тела находим, используя цилиндрические координаты:
- •Решение. Найдем массу рассматриваемого тела:
- •12.3. Задачи
12. Кратные интегралы
12.1. Двойной интеграл
Двойным
интегралом
от функции
![]() по области
по области![]() называется предел интегральной суммы
при стремлении к нулю наибольшего из
диаметров
всех элементарных областей:
называется предел интегральной суммы
при стремлении к нулю наибольшего из
диаметров
всех элементарных областей:
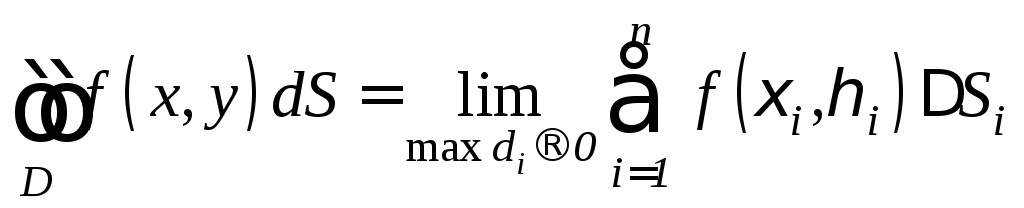 .
.
При вычислении
двойного интеграла в декартовых
координатах (тогда двойной интеграл,
как правило, записывается в виде
![]() ) различают следующие два случая.
) различают следующие два случая.

Рис. 12.1
Область интегрирования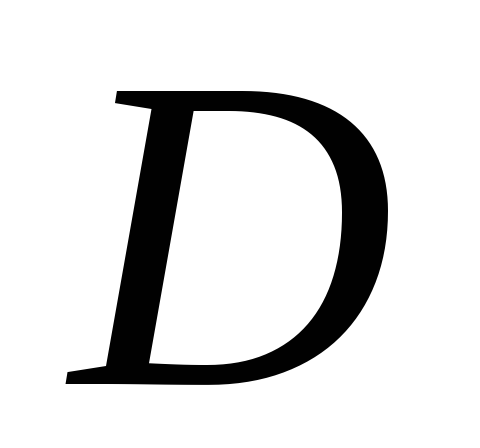 ограничена слева и справа прямыми
ограничена слева и справа прямыми и
и (
(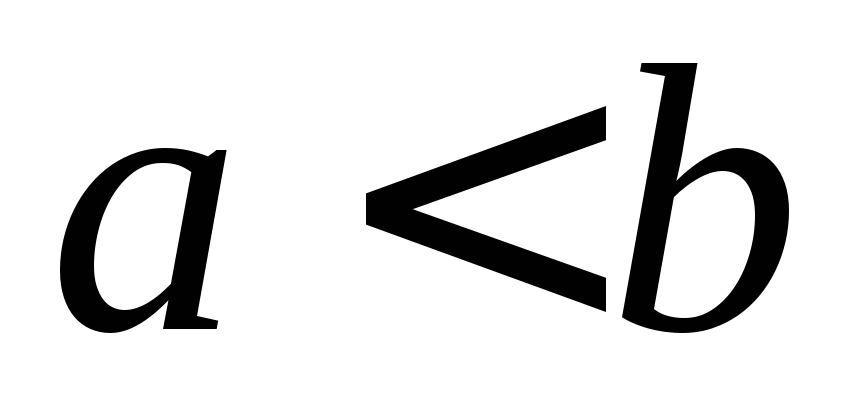 ),
а снизу и сверху – непрерывными кривыми
),
а снизу и сверху – непрерывными кривыми и
и ,
где
,
где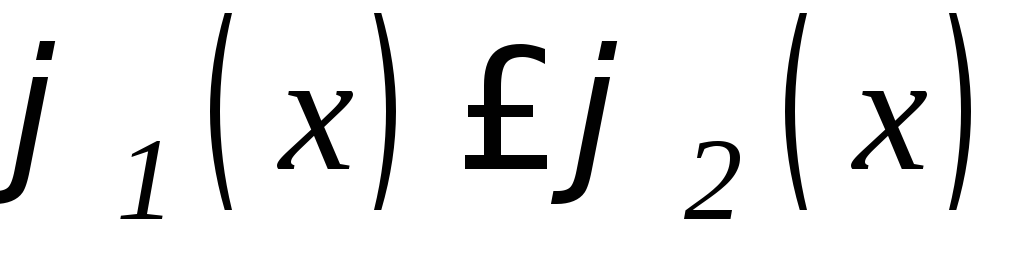 и каждая из кривых пересекается
вертикальной прямой только в одной
точке (рис. 12.1). Такая область называется
простой относительно оси
и каждая из кривых пересекается
вертикальной прямой только в одной
точке (рис. 12.1). Такая область называется
простой относительно оси .
.
Тогда вычисление двойного интеграла сводится к вычислению двукратного интеграла по формуле
 .
(12.1)
.
(12.1)
Здесь внутренний
интеграл
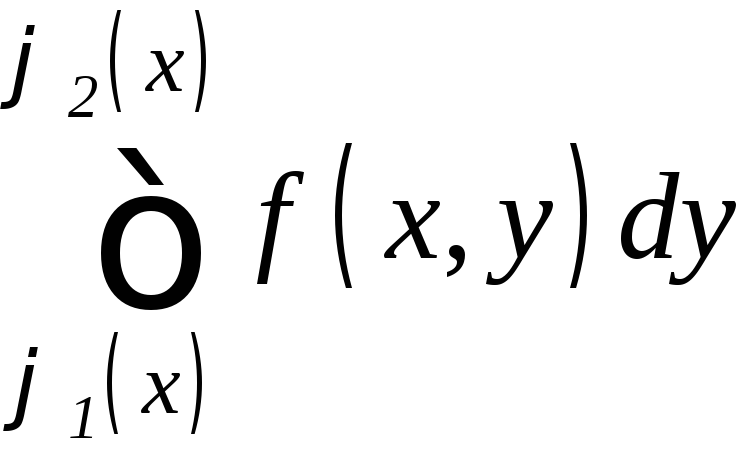 берется по переменной
берется по переменной![]() при фиксированном, но произвольном
значении
при фиксированном, но произвольном
значении![]() на отрезке
на отрезке![]() .
В результате получается некоторая
функция от
.
В результате получается некоторая
функция от![]() ,
которая затем интегрируется в пределах
от
,
которая затем интегрируется в пределах
от![]() до
до![]() .
.
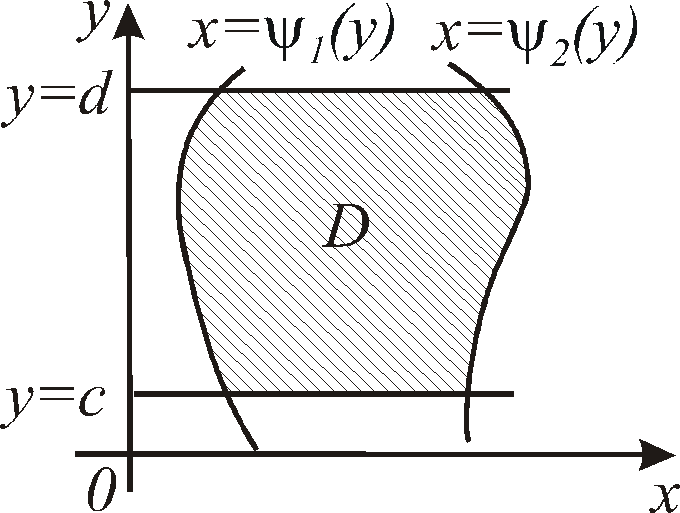
Рис. 12.2
Область интегрирования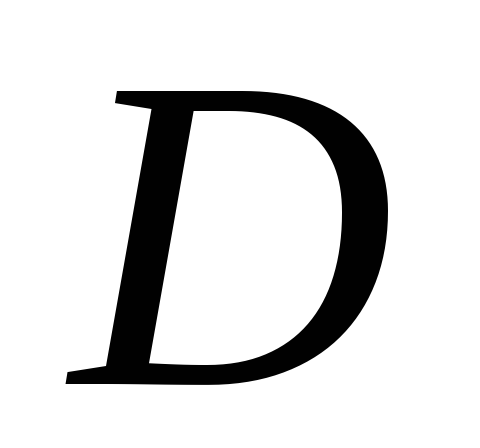 ограничена снизу и сверху прямыми
ограничена снизу и сверху прямыми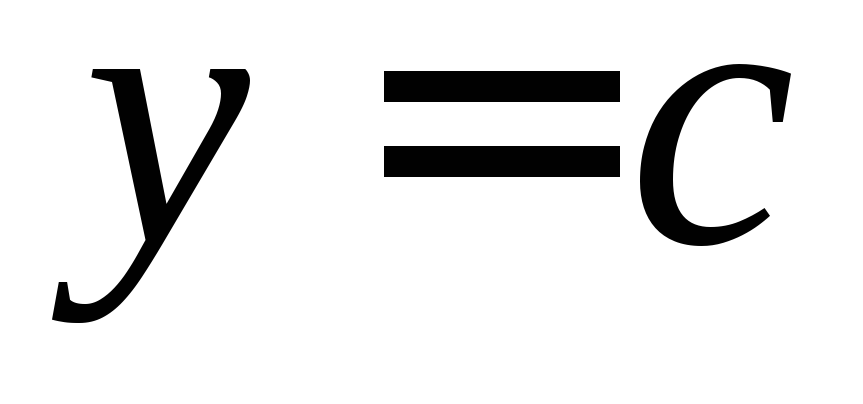 и
и (
( ),
а слева и справа – непрерывными кривыми
),
а слева и справа – непрерывными кривыми и
и ,
где
,
где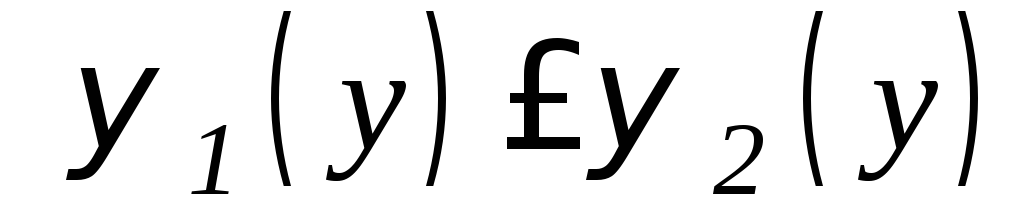 ,
каждая из кривых пересекается с
горизонтальной прямой только в одной
точке (рис. 12.2). Такая область называется
простой относительно оси
,
каждая из кривых пересекается с
горизонтальной прямой только в одной
точке (рис. 12.2). Такая область называется
простой относительно оси .
.
Для такой области двойной интеграл вычисляется по формуле
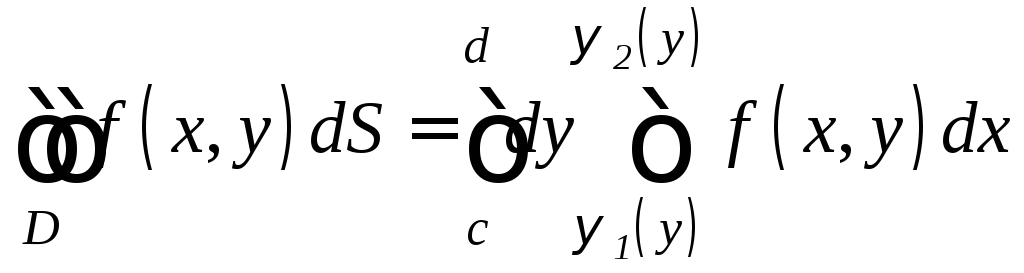 ,
(12.2)
,
(12.2)
причем сначала
вычисляется внутренний интеграл
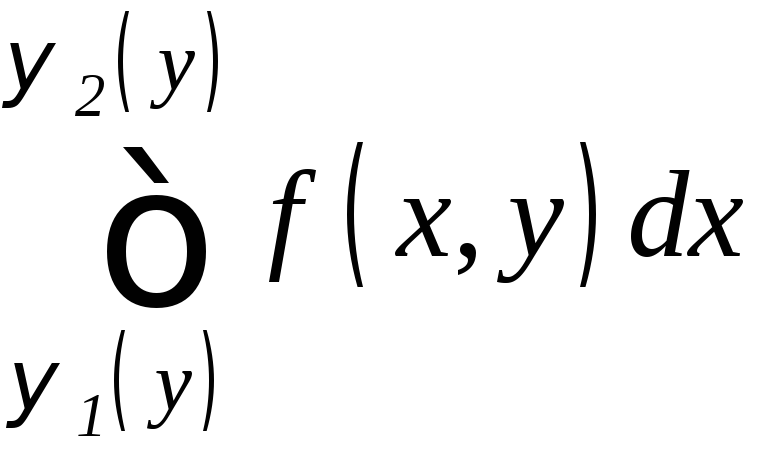 ,
в котором
,
в котором![]() считается постоянным.
считается постоянным.
В более общем случае область интегрирования путем разбиения на части сводится к основным областям.
Пример 1.
Вычислить двойной интеграл
![]() по области
по области![]() ,
ограниченной параболой
,
ограниченной параболой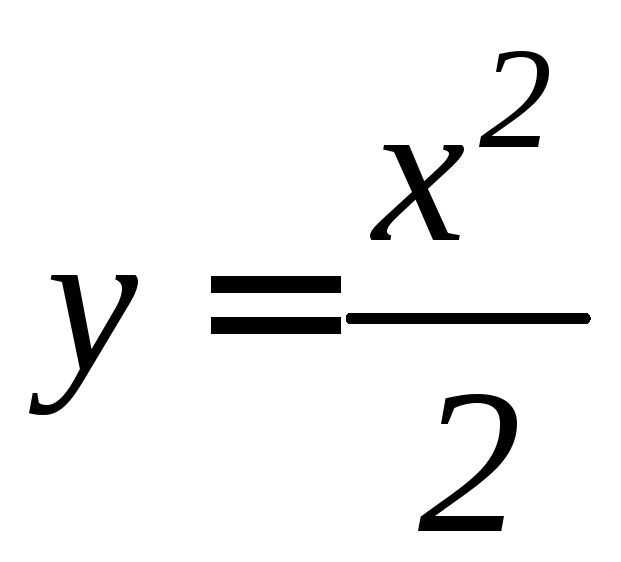 и прямыми
и прямыми![]()
![]() и
и![]() (рис. 12.3).
(рис. 12.3).
Рис. 12.3
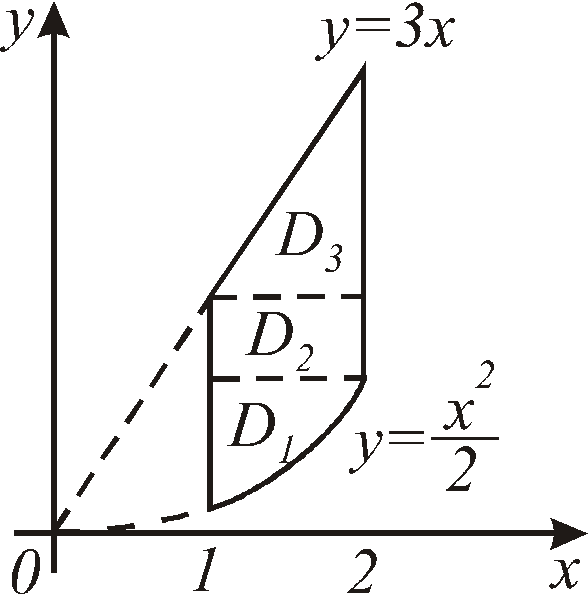
![]() является простой как относительно оси
является простой как относительно оси![]() ,
так и относительно оси
,
так и относительно оси![]() .
Однако левая и правая границы области
.
Однако левая и правая границы области![]() составлены из двух участков, поэтому
для вычисления интеграла по формуле
(12.2) необходимо разбить область
составлены из двух участков, поэтому
для вычисления интеграла по формуле
(12.2) необходимо разбить область![]() на три подобласти:
на три подобласти:![]() (рис. 12.3). В то же время нижняя и верхняя
границы представлены каждая своим
уравнением. Поэтому данный интеграл
удобнее вычислять по формуле (12.1):
(рис. 12.3). В то же время нижняя и верхняя
границы представлены каждая своим
уравнением. Поэтому данный интеграл
удобнее вычислять по формуле (12.1):
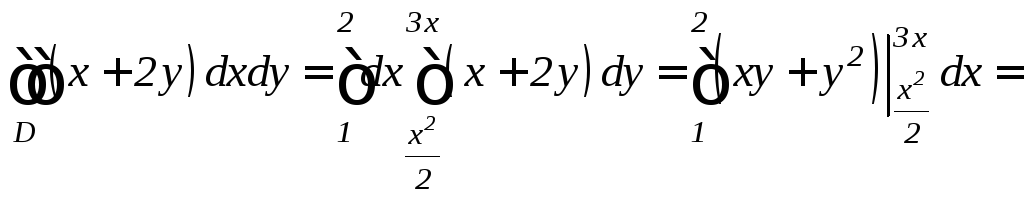
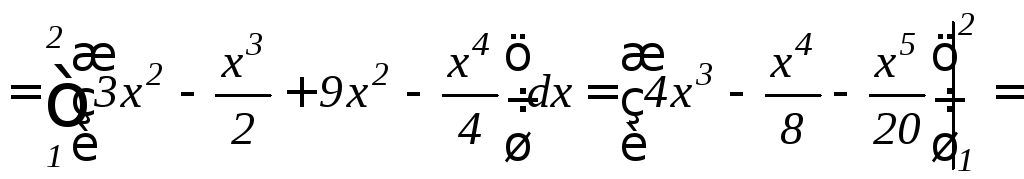
![]() .
.
Пример 2. Изменить порядок интегрирования в интеграле
 .
.
Рис. 12.4

![]() ограничена линиями
ограничена линиями![]() ,
,![]() ,
,![]() ,
,![]() (рис. 12.4). Изменим порядок интегрирования,
для чего заданную область представим
в виде двух подобластей
(рис. 12.4). Изменим порядок интегрирования,
для чего заданную область представим
в виде двух подобластей![]() ,
ограниченную слева и справа ветвями
параболы
,
ограниченную слева и справа ветвями
параболы![]() (
(![]() ),
и
),
и![]() ,
ограниченную дугами окружности
,
ограниченную дугами окружности![]() (
(![]() ).
Тогда
).
Тогда
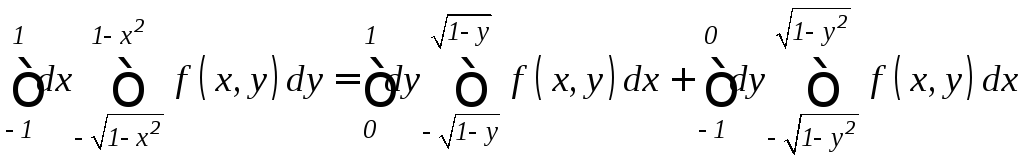 .
.
Иногда вычисление двойных интегралов упрощается с помощью замены переменных. Замена переменных в двойном интеграле производится по формуле
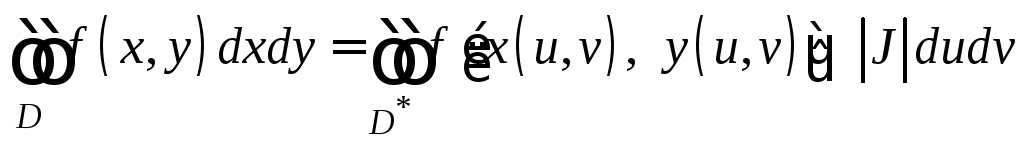 ,
(12.3)
,
(12.3)
где
![]() - область, в которую преобразуется
область
- область, в которую преобразуется
область![]() при отображении
при отображении![]() ,
,![]() ;
;![]() - подынтегральная функция, преобразованная
к новым координатам;
- подынтегральная функция, преобразованная
к новым координатам;![]() -якобиан
функций
-якобиан
функций
![]() ,
,![]() :
:
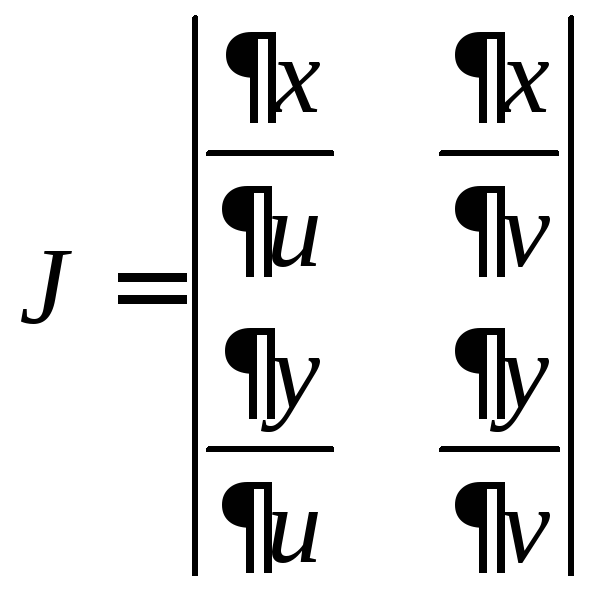 .
.
Часто используется
частный случай замены переменных –
полярные
координаты.
При этом в качестве
![]() и
и![]() берутся координаты
берутся координаты![]() и
и![]() ,
связанные с декартовыми формулами
,
связанные с декартовыми формулами
![]() ,
,
![]() (
(![]() ,
,![]() ).
).
Формула замены в этом случае переменных принимает вид
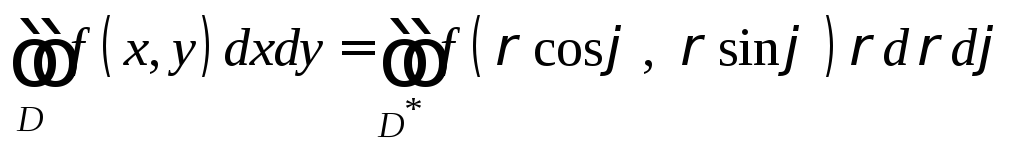 ,
(12.4)
,
(12.4)
где
![]() - область в полярной системе координат,
соответствующая области
- область в полярной системе координат,
соответствующая области![]() в декартовой системе координат.
в декартовой системе координат.
Пример 3.
Вычислить двойной интеграл
![]() ,
где
,
где![]() - область, ограниченная прямыми
- область, ограниченная прямыми![]() ,
,![]() ,
,![]() ,
,![]() (рис. 12.5).
(рис. 12.5).
